ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| СТАТИЧЕСКОЕ ДАВЛЕНИЕ И СКОРОСТНОЙ НАПОР УРАВНЕНИЕ БЕРНУЛЛИ
Самолет, находящийся в неподвижном или подвижном относительно него воздушном потоке, испытывает со стороны последнего давление, в первом случае (когда воздушный поток неподвижен) - это статическое давление и во втором случае (когда воздушный поток подвижен) - это динамическое давление, оно чаще называется скоростным напором. Статическое давление в струйке аналогично давлению покоящейся жидкости (вода, газ). Например: вода в трубе, она может находиться в состоянии покоя или движения, в обоих случаях стенки трубы испытывают давление со стороны воды. В случае движения воды давление будет несколько меньше, так как появился скоростной напор. Согласно закону сохранения энергии, энергия струйки воздушного потока в различных сечениях струйки воздуха есть сумма кинетической энергии потока, потенциальной энергии сил давления, внутренней энергии потока и энергии положения тела. Эта сумма - величина постоянная: Екин+Ер+Евн+Еп=сопst (1.10) Кинетическая энергия (Екин) - способность движущегося воздушного потока совершать работу. Она равна
где m- масса воздуха, кгс с2м; V-скорость воздушного потока, м/с. Если вместо массы m подставить массовую плотность воздуха р, то получим формулу для определения скоростного напора q (в кгс/м2)
Потенциальная энергия Ер - способность воздушного потока совершать работу под действием статических сил давления. Она равна (в кгс-м) Ep=PFS, (1.13) где Р - давление воздуха, кгс/м2; F - площадь поперечного сечения струйки воздушного потока, м2; S - путь, пройденный 1 кг воздуха через данное сечение, м; произведение SF называется удельным объемом и обозначается v, подставляя значение удельного объема воздуха в формулу (1.13), получим Ep=Pv.(1.14) Внутренняя энергия Евн - это способность газа совершать работу при изменении его температуры:
где Cv - теплоемкость воздуха при неизменном объеме, кал/кг-град; Т-температура по шкале Кельвина, К; А- термический эквивалент механической работы (кал-кг-м). Из уравнения видно, что внутренняя энергия воздушного потока прямо пропорциональна его температуре. Энергия положенияEn - способность воздуха совершать работу при изменении положения центра тяжести данной массы воздуха при подъеме на определенную высоту и равна En=mh (1.16) где h - изменение высоты, м. Ввиду мизерно малых значений разноса центров тяжести масс воздуха по высоте в струйке воздушного потока этой энергией в аэродинамике пренебрегают. Рассматривая во взаимосвязи все виды энергии применительно к определенным условиям, можно сформулировать закон Бернулли, который устанавливает связь между статическим давлением в струйке воздушного потока и скоростным напором. Рассмотрим трубу (Рис. 10) переменного диаметра (1, 2, 3), в которой движется воздушный поток. Для измерения давления в рассматриваемых сечениях используют манометры. Анализируя показания манометров, можно сделать заключение, что наименьшее динамическое давление показывает манометр сечения 3-3. Значит, при сужении трубы увеличивается скорость воздушного потока и давление падает.
Рис. 10 Объяснение закона Бернулли Причиной падения давления является то, что воздушный поток не производит никакой работы (трение не учитываем) и поэтому полная энергия воздушного потока остается постоянной. Если считать температуру, плотность и объем воздушного потока в различных сечениях постоянными (T1=T2=T3;р1=р2=р3, V1=V2=V3), то внутреннюю энергию можно не рассматривать. Значит, в данном случае возможен переход кинетической энергии воздушного потока в потенциальную и наоборот. Когда скорость воздушного потока увеличивается, то увеличивается и скоростной напор и соответственно кинетическая энергия данного воздушного потока. Подставим значения из формул (1.11), (1.12), (1.13), (1.14), (1.15) в формулу (1.10), учитывая, что внутренней энергией и энергией положения мы пренебрегаем, преобразуя уравнение (1.10), получим
Это уравнение для любого сечения струйки воздуха пишется следующим образом:
Такой вид уравнения является самым простым математическим уравнением Бернулли и показывает, что сумма статического и динамического давлений для любого сечения струйки установившегося воздушного потока есть величина постоянная. Сжимаемость в данном случае не учитывается. При учете сжимаемости вносятся соответствующие поправки. Для наглядности закона Бернулли можно провести опыт. Взять два листка бумаги, держа параллельно друг другу на небольшом расстоянии, подуть в промежуток между ними.
Рис. 11 Измерение скорости воздушного потока Листы сближаются. Причиной их сближения является то, что с внешней стороны листов давление атмосферное, а в промежутке между ними вследствие наличия скоростного напора воздуха давление уменьшилось и стало меньше атмосферного. Под действием разности давлений листки бумаги прогибаются вовнутрь. АЭРОДИНАМИЧЕСКИЕ ТРУБЫ Экспериментальная установка для исследования явлений и процессов, сопровождающих обтекание тел потоком газа называется аэродинамической трубой. Принцип действия аэродинамических труб основан на принципе относительности Галилея: вместо движения тела в неподвижной среде изучается обтекание неподвижного тела потоком газа В аэродинамических трубах экспериментально определяются действующие на ЛА аэродинамические силы и моменты исследуются распределения давления и температуры по его поверхности, наблюдается картина обтекания тела, изучается аэроупругость и т д. Аэродинамические трубы зависимости от диапазона чисел Маха М разделяются на дозвуковые (М=0,15-0,7), трансзвуковые (М=0,7-1 3), сверхзвуковые (М=1,3-5) и гиперзвуковые (М=5-25), по принципу действия - на компрессорные (непрерывного действия), в которых поток воздуха создается спец компрессором, и баллонные с повышенным давлением, по компоновке контура - на замкнутые и незамкнутые. Компрессорные трубы имеют высокий кпд, они удобны в работе, но требуют создания уникальных компрессоров с большими расходами газа и большой мощности. Баллонные аэродинамические трубы по сравнению с компрессорными менее экономичны, поскольку при дросселировании газа часть энергии теряется. Кроме того, продолжительность работы баллонных аэродинамических труб ограничена запасом газа в баллонах и составляет для различных аэродинамических труб от десятков секунд до несколько минут. Широкое распространение баллонных аэродинамических труб обусловлено тем, что они проще по конструкции а мощности компрессоров, необходимые для наполнения баллонов, относительно малы. В аэродинамических трубах с замкнутым контуром используется значительная часть кинетической энергии, оставшейся в газовом потоке после его прохождения через рабочую область, что повышает КПД трубы. При этом, однако, приходится увеличивать общие размеры установки. В дозвуковых аэродинамических трубах исследуются аэродинамические характеристики дозвуковых самолетов вертолетов а также характеристики сверхзвуковых самолетов на взлетно-посадочных режимах. Кроме того, они используются для изучения обтекания автомобилей и др. наземных транспортных средств, зданий, монументов, мостов и др. объектов На рис показана схема дозвуковой аэродинамической трубы с замкнутым контуром.
Рис. 12 Схема дозвуковой компрессорной аэродинамической трубы. 1- хонейкомб 2 - сетки 3 - форкамера 4 - конфузор 5 - направление потока 6 - рабочая часть с моделью 7 - диффузор, 8 - колено с поворотными лопатками, 9 - компрессор 10 - воздухоохладитель
Рис. 13 Схема баллонной трансзвуковой эжекторной аэродинамической трубы 1 - хонейкомб 2 - сетки 3 - форкамера 4 конфузор 5 перфорированная рабочая часть с моделью 6 эжектор 7 диффузор 8 колено с направляющими лопатками 9 выброс воздуха 10 - подвод воздуха от баллонов
Рис. 14 Схема сверхзвуковой баллонной аэродинамической трубы 1 - баллон со сжатым воздухом 2 - трубопровод 3 - регулирующий дроссель 4 - выравнивающие сетки 5 - хонейкомб 6 - детурбулизирующие сетки 7 - форкамера 8 - конфузор 9 - сверхзвуковое сопло 10 - рабочая часть с моделью 11 - сверхзвуковой диффузор 12 - дозвуковой диффузор 13 - выброс в атмосферу
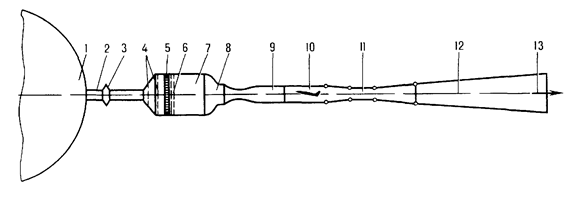
Рис. 15 Схема баллонной гиперзвуковой аэродинамической трубы 1 - баллон с высоким давлением 2 - трубопровод 3 - регулирующий дроссель 4 - подогреватель 5 - форкамера с хонейкомбом и сетками 6 - гиперзвуковое осесимметричное сопло 7 - рабочая часть с моделью 8 - гиперзвуковой осесимметричный диффузор 9 - воздухоохладитель 10 - направление потока 11 - подвод воздуха в эжекторы 12 - эжекторы 13 - затворы 14 - вакуумная емкость 15 - дозвуковой диффузор
АЭРОДИНАМИЧЕСКИЕ СИЛЫ |



 (1.11)
(1.11)
 . (1.12)
. (1.12) (1.15)
(1.15)
 (1.17)
(1.17)