 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Парная линейная регрессия.
а) Есть два ряда наблюдений, необходимо для них построить уравнение линейной регрессии, и оценить качество подбора уравнения с помощью критерия Фишера и критериев Стьюдента.
Эти данные мы получили, используя лишь формулы из теоретической части и простейшие функции Excel. На этом рисунке отображены полученные значения, исходя из них можно сказать, что связь между фактором и результатом достаточно тесная, поскольку коэффициент корреляции достаточно близок к 1 (>0,7), изменения результата на 82,5% зависят от изменения учтенного в модели фактора (обратите внимание, что одни и те же данные рассчитаны здесь дважды, но обозначены по разному ( Уравнение регрессии имеет следующий вид: Поскольку табличные значения критерия Фишера и критерия Стьюдента (Fтабл=5,32, tтабл=2,306 при a=0,05) меньше чем фактические, полученные по данному уравнению регрессии, можно сказать, что статистически значимо и уравнение регрессии в целом, и коэффициент регрессии, и коэффициент регрессии. То есть, по всем параметрам уравнение регрессии подобрано достаточно хорошо, и связь между фактором и результатом можно выражать через линейную форму. Для более полного понимания представим этот же рисунок в несколько другом виде. Вместо результатов будут отражены формулы Excel.
После этого выбираем следующее: Сервис-Анализ данных-Регрессия.
Нажимаем ОК и в появившемся окне заполняем следующие данные: 1) входной интервал y – диапазон, содержащий данные по результативному признаку; 2) входной интервал x – диапазон, содержащий данные по факторному признаку; 3) метки – флажок, который указывает, содержит ли первая строка названия столбцов (результата и фактора); 4) константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении регрессии; 5) уровень надежности– флажок, позволяющий изменить уровень надежности, по умолчанию используется 95%; 6) выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором разместиться результат; 7) новый рабочий лист – результат может быть размещен на новом листе, здесь же задается его название; Остальные флажки позволяют получить различные дополнительные данные и графики.
В нашем случае данные заполняются так, как это показано на рисунке. Полученный результат будет выглядеть следующим образом:
Соответственно, множественный R – это коэффициент корреляции, R-квадрат – это коэффициент детерминации, в таблице «Дисперсионный анализ» расположены по порядку число степеней свободы (регрессии, остатка, общее), сумма квадратов отклонений (регрессионная, остаточная и общая), дисперсия на 1 степень свободы (объясненная регрессией и остаточная), и критерий Фишера. В последней таблице находятся все значения по параметрам регрессии a и b. Их значения, стандартные ошибки, критерии Стьюдента, верхние и нижние границы доверительных интервалов при заданных различных уровнях надежности.
|
и 
), при выполнении задания дважды их рассчитывать не обязательно, мы сделали это для более полного понимания).
.
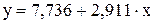Также при расчете парной линейной регрессии можно использовать инструмент «Регрессия» пакета анализа данных. С его помощью можно получить результаты регрессионной статистики, дисперсионного анализа и доверительные интервалы. Сначала необходимо проверить, что пакет анализа доступен. Для этого в меню Сервис выбираем команду Надстройки и в появившемся окне устанавливаем доступ к пакету анализа (устанавливаем флажок на соответствующей строке):
