 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Абсолютная и условная сходимость
ЗНАКОПЕРЕМЕННЫЕ РЯДЫ 1.Знакочередующиеся и знакопеременные ряды. Теорема Лейбница. 2.Абсолютная и условная сходимость. Свойства абсолютно сходящихся рядов.
До сих пор мы рассматривали и изучали ряды с положительными членами. Перейдем к общему случаю. Будем рассматривать ряды, содержащие положительные и отрицательные члены. Такие ряды называются знакопеременными. Изучение знакопеременных рядов начнем с частного случая - знакочередующихся рядов.
Вопрос 1. Знакочередующиеся и знакопеременные ряды. Теорема Лейбница
Знакочередующиеся ряды О.1.1. Ряд, у которого два соседних члена имеют противоположные знаки, называется знакочередующимся.
Знакочередующийся ряд имеет вид
где an > 0 (n = 1,2,….) положительны.
Для знакочередующихся рядов существует достаточный признак сходимости, установленный в 1714 г. Лейбницем в письме к Бернулли.
Т.1.1.(признак Лейбница) Если члены знакочередующегося ряда (1) по абсолютной величине монотонно убывают, т.е. an > an+1, n = 1,2,…. и общий член ряда стремится к нулю, т.е.
то ряд (1)сходится и его сумма S удовлетворяет неравенствам 0 < S < a1. Замечание Исследование знакочередующегося ряда вида ‒ a1 + a2 ‒ a3 + a4 ‒ …… (2) сводится путем умножения всех его членов на (‒1) к исследованию ряда (1).
Ряды (1) и (2), для которых выполняются условия теоремы Лейбница, называются лейбницевскими.
Следствие (оценка остатка знакочередующегося ряда) Остаток rn лейбницевского ряда (1) имеет знак своего первого члена и меньше его по абсолютной величине, т.е. | rn | < an+1. Здесь идет речь о сумме остатка ряда (для сходящихся рядов: остаток ряда и сумма остатка понимаются как одно и тоже).
Полученное неравенство используется в приближенных вычислениях для подсчета абсолютной ошибки замены суммы ряда ее частичной суммой. Иначе говоря, ошибка, совершаемая при замене S на Sn, меньше по абсолютной величине первого из отброшенных членов ряда.
Пример 1. Исследовать на сходимость ряд Решение 1. Для "nÎN: 2. Вывод: на основании теоремы Лейбница данный ряд сходится.
Рассмотренные знакочередующиеся ряды являются частным случаем знакопеременных рядов. Знакопеременные ряды
О.1.2. Числовой ряд
имеющий как положительные, так и отрицательные члены, расположенные в произвольном порядке, называется знакопеременным.
Каждому знакопеременному ряду (3) можно сопоставить положительный ряд, составленный из абсолютных величин членов ряда (3), т.е. ряд вида
Т.1.2. (достаточный признак сходимости знакопеременного ряда) Если сходится ряд (4), составленный из абсолютных величин членов ряда (3), то сходится и данный знакопеременный ряд (3). Замечание Обратное утверждение неверно: если сходится ряд (3), то это не означает, что будет сходиться и ряд (4).
Вопрос 2. Абсолютная и условная сходимость. Свойства абсолютно сходящихся Рядов
Абсолютная и условная сходимость
О.2.1. Знакопеременный ряд (3) называется абсолютно сходящимся, если сходится ряд (4), составленный из абсолютных величин членов ряда (3).
О.2.2. Знакопеременный ряд (3) называется условно сходящимся, если сам он сходится, а ряд (4), составленный из абсолютных величин членов ряда (3), расходится. Пример 2.
|



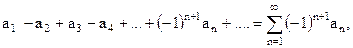 (1)
(1)

 т.е. an > an+1 Þ первое условие теоремы Лейбница выполнено.
т.е. an > an+1 Þ первое условие теоремы Лейбница выполнено. Þ второе условие теоремы Лейбница выполнено.
Þ второе условие теоремы Лейбница выполнено. (3)
(3) (4)
(4) является абсолютно сходящимся, так как ряд, составленный из модулей его членов ‒
является абсолютно сходящимся, так как ряд, составленный из модулей его членов ‒  сходится (см. пример 3 §2).
сходится (см. пример 3 §2). является условно сходящимся, так как сам он сходится (см. пример 1), а ряд, составленный из модулей его членов ‒
является условно сходящимся, так как сам он сходится (см. пример 1), а ряд, составленный из модулей его членов ‒  (гармонический ряд) – расходится.
(гармонический ряд) – расходится.