 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Ситуационная (практическая) задача № 1 12
По 20 предприятиям региона изучается зависимость выработки продукции на одного работника
Требуется: 1. Построить корреляционное поле между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации. Выдвинуть гипотезу о тесноте и виде зависимости между показателями
Выдвигаем гипотезу о линейной тесной прямой взаимосвязи. 2. Оценить тесноту линейной связи между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации с надежностью 0,9. Коэффициент корреляции:
Вводим гипотезы: Н0: Коэффициент корреляции не значим. Н1: Коэффициент корреляции значим. Гипотезу Н0 принимаем при выполнении условия
3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости выработки продукции на одного работника от удельного веса рабочих высокой квалификации.
4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы.
Вводим гипотезы: Н0: Коэффициенты уравнения не значимы. Н1: Коэффициенты уравнения значимы. Гипотезу Н0 принимаем при выполнении условия
Доверительные интервалы для коэффициентов регрессии:
С вероятностью 95% коэффициент
С вероятностью 90% коэффициент 5. Рассчитать коэффициент детерминации. С помощью F - критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9. Коэффициент детерминации для линейной модели:
Вводим гипотезы: Н0: Уравнение регрессии не значимо. Н1: Уравнение регрессии значимо. Гипотезу Н0 принимаем при выполнении условия:
6. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих. Точечный прогноз:
Интервальный прогноз:
С вероятностью 90% прогнозное значение находится в интервале от 9,36 до 11,88 тыс. руб., если на высокую квалификацию имеют 24% рабочих.
7. Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров. Множественная зависимость:
Вектор оценок параметров линейной модели размера по формуле:
Метод наименьших квадратов:
При увеличении стоимости фондов на конец года на 1% выработка продукции на одного работника увеличивается на 0,016 тыс. руб., а при увеличении ввода в действие новых основных фондов на 1% выработка продукции на одного работника увеличивается на 1,338 тыс. руб.
8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы.
Вводим гипотезы: Н0: Коэффициенты уравнения не значимы. Н1: Коэффициенты уравнения значимы. Гипотезу Н0 принимаем при выполнении условия
Матрица
Доверительные интервалы для коэффициентов регрессии:
С вероятностью 90% коэффициент
С вероятностью 90% коэффициент
С вероятностью 90% коэффициент
9. Найти коэффициенты парной и частной корреляции. Проанализировать их. Парные коэффициенты корреляции:
Расчет частных коэффициентов корреляции:
Коэффициенты парной и частной корреляции свидетельствуют о сильной прямой взаимосвязи между Х1 и Y и слабой взаимосвязи между Х2 и Y.
10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
Коэффициент множественной детерминации (общий):
Скорректированный коэффициент множественной детерминации:
Скорректированный коэффициент множественной детерминации и общий коэффициентом детерминации различаются незначительно.
11. С помощью F - критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9. Вводим гипотезы: Н0: Уравнение регрессии не значимо. Н1: Уравнение регрессии значимо. Гипотезу Н0 принимаем при выполнении условия:
12. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%.
Интервальный прогноз:
С вероятностью 90% выработки продукции на одного работника будет в интервале от 7,442 до 9,35 тыс. руб., если высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%.
13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты.
Вводим гипотезы: Н0: мультиколлинеарности нет. Н1: мультиколлинеарность есть. Критерий Стьюдента. Гипотезу Н0 принимаем при выполнении условия
Критерий χ2. Гипотезу Н0 принимаем при выполнении условия
12 |



 (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих
(тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих  (% от стоимости фондов на конец года) и от ввода в действие новых основных фондов
(% от стоимости фондов на конец года) и от ввода в действие новых основных фондов  (%).
(%).


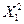




 , следует принимаем гипотезу Н1. С вероятностью 90% коэффициент корреляции значим.
, следует принимаем гипотезу Н1. С вероятностью 90% коэффициент корреляции значим.


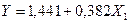



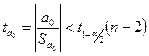







 , следует принимаем гипотезу Н1. С вероятностью 90% коэффициент
, следует принимаем гипотезу Н1. С вероятностью 90% коэффициент  значим.
значим. , следует принимаем гипотезу Н1. С вероятностью 90% коэффициент
, следует принимаем гипотезу Н1. С вероятностью 90% коэффициент  значим.
значим.


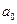 находится в интервале от 0,343 до 0,421.
находится в интервале от 0,343 до 0,421.

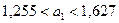



 , следует принимаем гипотезу Н1. С вероятностью 90% уравнение регрессии значимо.
, следует принимаем гипотезу Н1. С вероятностью 90% уравнение регрессии значимо. тыс. руб.
тыс. руб.



 где a0, a1, a2 - неизвестные параметры,
где a0, a1, a2 - неизвестные параметры,  - случайное отклонение.
- случайное отклонение.














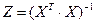
 , следует принимаем гипотезу Н1. С вероятностью 90% коэффициент
, следует принимаем гипотезу Н1. С вероятностью 90% коэффициент  , следует принимаем гипотезу Н0. С вероятностью 90% коэффициент
, следует принимаем гипотезу Н0. С вероятностью 90% коэффициент  , следует принимаем гипотезу Н1. С вероятностью 90% коэффициент
, следует принимаем гипотезу Н1. С вероятностью 90% коэффициент  значим.
значим.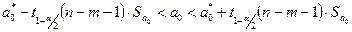








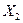
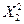



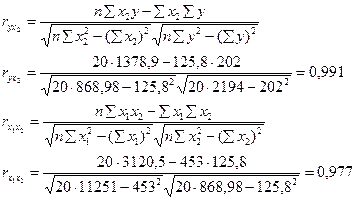
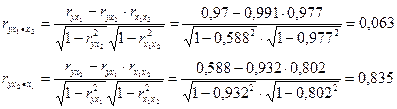

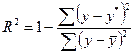




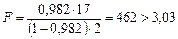 , следует принимаем гипотезу Н1. С вероятностью 90% уравнение регрессии значимо.
, следует принимаем гипотезу Н1. С вероятностью 90% уравнение регрессии значимо. тыс. руб.
тыс. руб.

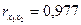


 следует принимаем гипотезу Н1. С вероятностью 90% мультиколлинеарность есть.
следует принимаем гипотезу Н1. С вероятностью 90% мультиколлинеарность есть.


 следует принимаем гипотезу Н1. С вероятностью 90% мультиколлинеарность есть.
следует принимаем гипотезу Н1. С вероятностью 90% мультиколлинеарность есть.