 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ЯДЕРНАЯ ФИЗИКА»
Задача 1.Определите число нуклонов А и порядковый номер Z элемента, образующегося при двух α-превращениях и двух β-превращениях урана  . . | Дано: 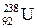 , a, b Найти: А ― ? Z ― ? , a, b Найти: А ― ? Z ― ? | Решение. При решении задачи воспользуемся законами сохранения массового и зарядового чисел. В результате двух a-распадов 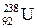 ® ®  + +  + +  . Получается дочернее ядро . Получается дочернее ядро  . Рассмотрим β-распад: . Рассмотрим β-распад:  ® ®  + +  ® ®  + +  + +  . Итак, число нуклонов конечного ядра А = 230, число протонов Z = 90, число нейтронов 140. По таблице находим, что это изотоп тория: . Итак, число нуклонов конечного ядра А = 230, число протонов Z = 90, число нейтронов 140. По таблице находим, что это изотоп тория:  . . . . | Задача 2.Определите, в ядро атома какого элемента превращается ядро полония  при испускании a-частицы. при испускании a-частицы. | Дано:  . a-частица Найти6. X ― ? . a-частица Найти6. X ― ? | Решение.Запишем ядерное превращение:  ® ®  + +  . Из законов сохранения зарядового и массового чисел получим: А = 218 – 4 = 214, Z = 84 – 2 = 82. Полученный элемент ― свинец . Из законов сохранения зарядового и массового чисел получим: А = 218 – 4 = 214, Z = 84 – 2 = 82. Полученный элемент ― свинец  | Задача 3.Определите энергию связи и удельную энергию связи в ядре атома ртути  . Масса покоя ядра 200,028 а. е. м. . Масса покоя ядра 200,028 а. е. м. | Дано:  . mя = 200,028 а. е. м. Массы покоя протона и нейтрона mn = 1,00899 а. е. м.; mp = 1,00814 а. е. м. Найти: . mя = 200,028 а. е. м. Массы покоя протона и нейтрона mn = 1,00899 а. е. м.; mp = 1,00814 а. е. м. Найти:  | Решение. Число протонов в ядре HgZ = 80, число нейтронов N = 200 – 80 = 120. Дефект масс определим по формуле Dm = 80 × 1,00814 + 120 × 1,00899 – 200,028 = 1,702 а. е. м. Отсюда, зная, что 1 а. е. м. = 931  , энергия связи равна DEсв ≈ 1585 МэВ, DEсв.уд = , энергия связи равна DEсв ≈ 1585 МэВ, DEсв.уд =  , DEсв.уд = , DEсв.уд =   ≈ 7,93 ≈ 7,93  . . | Задача 4.Определите энергию, выделяющуюся при ядерной реакции  + +  ® 2( ® 2(  ). Удельная энергия связи у ядра атома изотопа лития 5,6 ). Удельная энергия связи у ядра атома изотопа лития 5,6  , у гелия ― 7,075 , у гелия ― 7,075  . . | Дано:  = 5,6 = 5,6  ; ;  = 7,075 = 7,075  Найти: DE ― ? Найти: DE ― ? | Решение. Выделенная энергия равна разности энергий связи Li и He. DE = 2  × AHe – × AHe –  ALi = (2 × 7,075 × 4 – 5,6 × 7) = (56,6 – 39,2) = 17,4 (МэВ).. ALi = (2 × 7,075 × 4 – 5,6 × 7) = (56,6 – 39,2) = 17,4 (МэВ).. | Задача 5.Определите, в какой момент времени число нераспавшихся ядер изотопа  станет равным 1011, если в начальный момент число ядер равно 1022. Период полураспада равен 5730 лет. станет равным 1011, если в начальный момент число ядер равно 1022. Период полураспада равен 5730 лет. | Дано: N0 = 1022. N = 1011.  = 5730 лет. Найти: t ― ? = 5730 лет. Найти: t ― ? | Решение. Формула закона радиоактивного распада имеет вид: N = N0 ×  . Откуда t = . Откуда t =  . Подставив значения T, N0, N, имеем: t = . Подставив значения T, N0, N, имеем: t =  ≈ 2,09 × 105 (лет). Окончательно имеем: t = 2,09 × 105 лет. ≈ 2,09 × 105 (лет). Окончательно имеем: t = 2,09 × 105 лет. | | | | | | | Задача 1.Определите число нуклонов А и порядковый номер Z элемента, образующегося при двух α-превращениях и двух β-превращениях урана  . . | Дано: 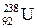 , a, b Найти: А ― ? Z ― ? , a, b Найти: А ― ? Z ― ? | Анализ.При решении задачи воспользуемся законами сохранения массового и зарядового чисел. Решение.В результате двух a-распадов 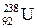 ® ®  + +  + +  . Получается дочернее ядро . Получается дочернее ядро  . Рассмотрим β-распад: . Рассмотрим β-распад:  ® ®  + +  ® ®  + +  + +  . Итак, число нуклонов конечного ядра А = 230, число протонов Z = 90, число нейтронов 140. По таблице находим, что это изотоп тория: . Итак, число нуклонов конечного ядра А = 230, число протонов Z = 90, число нейтронов 140. По таблице находим, что это изотоп тория:  . Ответ: . Ответ:  . . | Задача 2.Определите, в ядро атома какого элемента превращается ядро полония  при испускании a-частицы. при испускании a-частицы. | Дано:  . a-частица Найти6. X ― ? . a-частица Найти6. X ― ? | Анализ.При решении задачи воспользуемся законами сохранения массового и зарядового чисел. Решение.Запишем ядерное превращение:  ® ®  + +  . Из законов сохранения зарядового и массового чисел получим: А = 218 – 4 = 214, Z = 84 – 2 = 82. Полученный элемент ― свинец . Из законов сохранения зарядового и массового чисел получим: А = 218 – 4 = 214, Z = 84 – 2 = 82. Полученный элемент ― свинец  . Ответ: . Ответ:  . . | Задача 3.Определите энергию связи и удельную энергию связи в ядре атома ртути  . Масса покоя ядра 200,028 а. е. м. . Масса покоя ядра 200,028 а. е. м. | Дано:  . mя = 200,028 а. е. м. Массы покоя протона и нейтрона mn = 1,00899 а. е. м.; mp = 1,00814 а. е. м. Найти: . mя = 200,028 а. е. м. Массы покоя протона и нейтрона mn = 1,00899 а. е. м.; mp = 1,00814 а. е. м. Найти:  | Анализ.Энергия связи связана с дефектом масс соотношением  . Поэтому, вычислив дефект масс, мы можем определить энергию связи ядра. Затем, разделив эту энергию на массовое число, мы определим удельную энергию связи. Решение. Число протонов в ядре HgZ = 80, число нейтронов N = 200 – 80 = 120. Дефект масс определим по формуле Dm = 80 × 1,00814 + 120 × 1,00899 – 200,028 = 1,702 а. е. м. Отсюда, зная, что 1 а. е. м. = 931 . Поэтому, вычислив дефект масс, мы можем определить энергию связи ядра. Затем, разделив эту энергию на массовое число, мы определим удельную энергию связи. Решение. Число протонов в ядре HgZ = 80, число нейтронов N = 200 – 80 = 120. Дефект масс определим по формуле Dm = 80 × 1,00814 + 120 × 1,00899 – 200,028 = 1,702 а. е. м. Отсюда, зная, что 1 а. е. м. = 931  , энергия связи равна DEсв ≈ 1585 МэВ, DEсв.уд = , энергия связи равна DEсв ≈ 1585 МэВ, DEсв.уд =  , DEсв.уд = , DEсв.уд =   ≈ 7,93 ≈ 7,93  . Ответ: 1585 МэВ, 7,93 . Ответ: 1585 МэВ, 7,93  . . |
Задача 4.Определите энергию, выделяющуюся при ядерной реакции  + +  ® 2( ® 2(  ). Удельная энергия связи у ядра атома изотопа лития 5,6 ). Удельная энергия связи у ядра атома изотопа лития 5,6  , у гелия ― 7,075 , у гелия ― 7,075  . . | Дано:  = 5,6 = 5,6  ; ;  = 7,075 = 7,075  Найти: DE ― ? Найти: DE ― ? | Анализ.При ядерных реакциях энергия сохраняется. Поэтому, если суммарная энергия образовавшихся частиц меньше суммарной энергии частиц, вступивших в реакцию, то энергия выделяется при реакции и равна их разности. Решение. Выделенная энергия равна разности энергий связи Li и He. DE = 2  × AHe – × AHe –  ALi = (2 × 7,075 × 4 – 5,6 × 7) = (56,6 – 39,2) = 17,4 (МэВ). Ответ: 17,4 МэВ. ALi = (2 × 7,075 × 4 – 5,6 × 7) = (56,6 – 39,2) = 17,4 (МэВ). Ответ: 17,4 МэВ. | Задача 5.Определите, в какой момент времени число нераспавшихся ядер изотопа  станет равным 1011, если в начальный момент число ядер равно 1022. Период полураспада равен 5730 лет. станет равным 1011, если в начальный момент число ядер равно 1022. Период полураспада равен 5730 лет. | Дано: N0 = 1022. N = 1011.  = 5730 лет. Найти: t ― ? = 5730 лет. Найти: t ― ? | Анализ.Закон радиоактивного распада описывается формулой, по которой можно посчитать число нераспавшихся ядер в любой момент времени, зная начальное число ядер и период полураспада. Здесь мы решаем обратную задачу: определяем в какой момент времени число нераспавшихся ядер равно заданному числу. Решение. Формула закона радиоактивного распада имеет вид: N = N0 ×  . Откуда t = . Откуда t =  . Подставив значения T, N0, N, имеем: t = . Подставив значения T, N0, N, имеем: t =  ≈ 2,09 × 105 (лет). Окончательно имеем: t = 2,09 × 105 лет. Ответ: 2,09 × 105 лет. ≈ 2,09 × 105 (лет). Окончательно имеем: t = 2,09 × 105 лет. Ответ: 2,09 × 105 лет. |
|




 .
.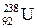 , a, b Найти: А ― ? Z ― ?
, a, b Найти: А ― ? Z ― ? +
+  +
+  +
+  ®
®  +
+  . .
. . при испускании a-частицы.
при испускании a-частицы. . Из законов сохранения зарядового и массового чисел получим: А = 218 – 4 = 214, Z = 84 – 2 = 82. Полученный элемент ― свинец
. Из законов сохранения зарядового и массового чисел получим: А = 218 – 4 = 214, Z = 84 – 2 = 82. Полученный элемент ― свинец 
 . Масса покоя ядра 200,028 а. е. м.
. Масса покоя ядра 200,028 а. е. м.
 , энергия связи равна DEсв ≈ 1585 МэВ, DEсв.уд =
, энергия связи равна DEсв ≈ 1585 МэВ, DEсв.уд =  , DEсв.уд =
, DEсв.уд = 
 ≈ 7,93
≈ 7,93  .
. +
+  ® 2(
® 2(  , у гелия ― 7,075
, у гелия ― 7,075  .
. = 5,6
= 5,6  ;
;  = 7,075
= 7,075  ALi = (2 × 7,075 × 4 – 5,6 × 7) = (56,6 – 39,2) = 17,4 (МэВ)..
ALi = (2 × 7,075 × 4 – 5,6 × 7) = (56,6 – 39,2) = 17,4 (МэВ).. станет равным 1011, если в начальный момент число ядер равно 1022. Период полураспада равен 5730 лет.
станет равным 1011, если в начальный момент число ядер равно 1022. Период полураспада равен 5730 лет. = 5730 лет. Найти: t ― ?
= 5730 лет. Найти: t ― ? . Откуда t =
. Откуда t =  . Подставив значения T, N0, N, имеем: t =
. Подставив значения T, N0, N, имеем: t =  ≈ 2,09 × 105 (лет). Окончательно имеем: t = 2,09 × 105 лет.
≈ 2,09 × 105 (лет). Окончательно имеем: t = 2,09 × 105 лет. . Поэтому, вычислив дефект масс, мы можем определить энергию связи ядра. Затем, разделив эту энергию на массовое число, мы определим удельную энергию связи. Решение. Число протонов в ядре HgZ = 80, число нейтронов N = 200 – 80 = 120. Дефект масс определим по формуле Dm = 80 × 1,00814 + 120 × 1,00899 – 200,028 = 1,702 а. е. м. Отсюда, зная, что 1 а. е. м. = 931
. Поэтому, вычислив дефект масс, мы можем определить энергию связи ядра. Затем, разделив эту энергию на массовое число, мы определим удельную энергию связи. Решение. Число протонов в ядре HgZ = 80, число нейтронов N = 200 – 80 = 120. Дефект масс определим по формуле Dm = 80 × 1,00814 + 120 × 1,00899 – 200,028 = 1,702 а. е. м. Отсюда, зная, что 1 а. е. м. = 931  , энергия связи равна DEсв ≈ 1585 МэВ, DEсв.уд =
, энергия связи равна DEсв ≈ 1585 МэВ, DEсв.уд =