 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Среднее квадратическое отклонение, что оно характеризует. 12
Среднее квадратическое отклонение характеризует среднее отклонение всех вариант вариационного ряда от средней арифметической величины. Поскольку отклонения вариант от средней, имеют значения с «+» и «-», то при суммировании они взаимоуничтожаются. Чтобы избежать этого, отклонения возводятся во вторую степень, а затем, после определенных вычислений, производится обратное действие — извлечение корня квадратного. Поэтому среднее отклонение именуется квадратическим. Среднее квадратическое отклонение для несгруппированных данных для вариационного ряда Среднее квадратическое отклонение — это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется. Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной будет средняя величина. Коэффициент корреляции. Коэффициент корреляции — это величина, которая может варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной — минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:
В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака приближается к нулю:
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга. В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значениями коэффициента корреляции Браве-Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. n-2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Хотелось бы еще раз подчеркнуть, что сущность этих двух коэффициентов несколько различна. Отрицательный коэффициент r указывает на то, что эффективность чаще всего тем выше, чем время реакции меньше, тогда как при вычислении коэффициента rs требовалось проверить, всегда ли более быстрые испытуемые реагируют более точно, а более медленные — менее точно. Коэффициент корреляции Браве-Пирсона (r) — это параметрический показатель, для вычисления которого сравнивают средние и стандартные отклонения результатов двух измерений. При этом используют формулу (у разных авторов она может выглядеть по-разному)
где ΣXY — сумма произведений данных из каждой пары; n-число пар; X — средняя для данных переменной X; Y— средняя для данных переменной Y; Sx — стандартное отклонение для распределения х; Sy — стандартное отклонение для распределения у. Коэффициент корреляции рангов Спирмена (rs) — это непараметрический показатель, с помощью которого пытаются выявить связь между рангами соответственных величин в двух рядах измерений. Этот коэффициент рассчитывать проще, однако результаты получаются менее точными, чем при использовании r. Это связано с тем, что при вычислении коэффициента Спирмена используют порядок следования данных, а не их количественные характеристики и интервалы между классами. Дело в том, что при использовании коэффициента корреляции рангов Спирмена (rs) проверяют только, будет ли ранжирование данных для какой-либо выборки таким же, как и в ряду других данных для этой выборки, попарно связанных с первыми. Если коэффициент близок к +1, то это означает, что оба ряда практически совпадают, а если этот коэффициент близок к -1, можно говорить о полной обратной зависимости. Коэффициент rs вычисляют по формуле
где d — разность между рангами сопряженных значений признаков (независимо от ее знака), а — число пар. Обычно этот непараметрический тест используется в тех случаях, когда нужно сделать какие-то выводы не столько об интервалах между данными, сколько об их рангах, а также тогда, когда кривые распределения слишком асимметричны и не позволяют использовать такие параметрические критерии, как коэффициент r (в этих случаях бывает необходимо превратить количественные данные в порядковые). 12 |



 равно корню квадратному из дисперсии:
равно корню квадратному из дисперсии: ,
,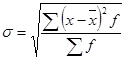 .
.



