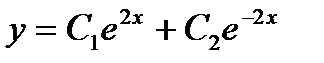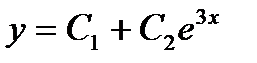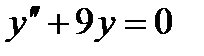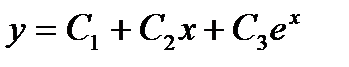ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| А) айнымалысы ажыратылатын 12
* А) біртекті теңдеу * A) * A) * A) * A) * A) * A) * A) * А) * A) * A) * A) * A) * A) * A) * A) * A) * A) * A) * A) 3 * A) 0 * A) * А) * A)
* А) *p – параметрінің қандай мәндерінде A) * A) * A) * A) * A) *
* A) * A) А *Ауыспа таңбалы A) A) * A) Г *Гармоникалық қатарды көрсетіңіз A) Д *Дәрежелік қатардың A) Е *Егер A) *Егер A) *Егер A) *Егер A) *Егер A) *Егер A) *Егер A) *Егер A) *Егер A) *Егер A) *Егер A) *Егер A) 0 *Егер A) *Егер A) *Егер A) *Егер А) толық дифференциалды теңдеу *Егер A) *Егер A) *Егер A) *Егер А) *Егер А) *Егер A) табаны * A) *Егер A) *Егер A) *Егер А) *Егер интегралдау аймағы А) *Егер сандық қатар A) *Егер A) *Егер A) *Егер A) *Егер дәрежелік A) *Егер А) жинақты *Егер А) И *Интегралды есептеңіз: А) 9 *Интегралды есептеңіз: А) 4 *Интегралды есептеңіз: А) 32 *Интегралды есептеңіз: А) 2/3 *Интегралды есептеңіз: А) *Интегралды есептеңіз: А) 4/3 *Интегралды есептеңіз: A) 8 $$$ 213 Интегралды есептеңіз: A) 9 *Интегралды есептеңіз: A) 8/3 *Интегралды есептеңіз: A) 7 *Интегралды есептеңіз: A) 8 *Интегралды есептеңіз: A) 2 *Интегралды есептеңіз: A) 2 *Интегралды есептеңіз: A) 1 $$$ 223 Интегралды есептеңіз: A) 2 *Интегралды есептеңіз: A) *Интегралды есептеңіз: A) 26 *Интегралды есептеңіз: A) 4 *Интегралды есептеңіз: A) 36 *Интегралды есептеңіз: A) 9/2 *Интегралды есептеңіз: A) 4 *Интегралды есептеңіз: A) 16/3 *Интегралды есептеңіз: A) 16/3 *Интегралды есептеңіз: A) 18 *Интегралды есептеңіз: A) 3 *Интегралды есептеңіз: A) *Интегралды есептеңіз: A) 6 *Интегралды есептеңіз: A) 16 *Интегралды есептеңіз: A) 2 *Интегралды есептеңіз: A) *Интегралды есептеңіз: A) 4 *Интегралды есептеңіз: A) $$$ 243 Интегралды есептеңіз: А) 3 *Интегралды есептеңіз: А) 6 *Интегралды есептеңіз: А) *Интегралды есептеңіз: А) 9 *Интегралды есептеңіз: A) Қ *Қатар жинақтылығының Коши белгісін көрсетіңіз A) *Қатар жинақтылығының Даламбер белгісін көрсетіңіз A) М *Мына A) П *Параметрлік теңдеумен берілген A) Т *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A)
*Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) *Теңдеуді шешіңіз: A) Ф *Функциялық қатарды көрсетіңіз A)
12 |



 - бірінші реттік дифференциалдық теңдеуін қандай теңдеу деп атайды?
- бірінші реттік дифференциалдық теңдеуін қандай теңдеу деп атайды? ,
,  - Бернулли теңдеуін сызықты бірінші ретті дифференциалдық теңдеуге келтіретін алмастыруды белгілеңіз
- Бернулли теңдеуін сызықты бірінші ретті дифференциалдық теңдеуге келтіретін алмастыруды белгілеңіз
 - теңдеуінің шешімін табыңыздар:
- теңдеуінің шешімін табыңыздар:
 ,
,  Коши есебін шешіңіз:
Коши есебін шешіңіз:
 ;
;  - Коши есебінің шешімін табыңыздар:
- Коши есебінің шешімін табыңыздар:
 - Коши есебінің шешімін табыңыздар:
- Коши есебінің шешімін табыңыздар:
 - Коши есебінің шешімін табыңыздар:
- Коши есебінің шешімін табыңыздар:
 - Коши есебінің шешімін табыңыздар:
- Коши есебінің шешімін табыңыздар:
 , мұнда
, мұнда  дифференциалдық теңдеуінің жалпы шешімі келесі түрде беріледі:
дифференциалдық теңдеуінің жалпы шешімі келесі түрде беріледі:
 ,
,  ,
,  - дифференциалдық теңдеуінің жалпы шешімі келесі түрде беріледі
- дифференциалдық теңдеуінің жалпы шешімі келесі түрде беріледі
 - теңдеуінің шешімін табыңыздар:
- теңдеуінің шешімін табыңыздар:
 - Коши есебінің шешімін табыңыздар:
- Коши есебінің шешімін табыңыздар: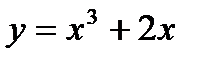
 - Коши есебінің шешімін табыңыздар:
- Коши есебінің шешімін табыңыздар:
 - Коши есебінің шешімін табыңыздар:
- Коши есебінің шешімін табыңыздар:
 - Коши есебінің шешімін табыңыздар:
- Коши есебінің шешімін табыңыздар:
 - Коши есебінің шешімін табыңыздар:
- Коши есебінің шешімін табыңыздар:
 - теңдеуінің шешімін табыңыздар:
- теңдеуінің шешімін табыңыздар:
 - дифференциалдық теңдеуінің жалпы шешімі неге тең?
- дифференциалдық теңдеуінің жалпы шешімі неге тең?
 - дифференциалдық теңдеуінің сипаттамалық теңдеуі қандай түрде жазылады?
- дифференциалдық теңдеуінің сипаттамалық теңдеуі қандай түрде жазылады?
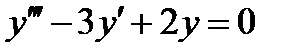 - дифференциалдық теңдеуінің сипаттамалық түбірлерінің қосындысы неге тең?
- дифференциалдық теңдеуінің сипаттамалық түбірлерінің қосындысы неге тең? - дифференциалдық теңдеуінің сипаттамалық түбірлерінің көбейтіндісі неге тең?
- дифференциалдық теңдеуінің сипаттамалық түбірлерінің көбейтіндісі неге тең? ,
,  қисығының доғасының ұзындығын есептеу керек
қисығының доғасының ұзындығын есептеу керек
 ,
,  ,
,  cызықтарымен шектелген жазықтықтың
cызықтарымен шектелген жазықтықтың  аймағының ауданын табыңыз:
аймағының ауданын табыңыз:
 сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді:
сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді:
 полярлық координаталарда
полярлық координаталарда  облысының ауданы қандай формуламен есептелінеді?
облысының ауданы қандай формуламен есептелінеді?
 - Дирихле қатары жинақты болады?
- Дирихле қатары жинақты болады?
 облысы
облысы  ,
, 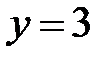 ,
,  ,
,  ,
,  беттерімен шектелген
беттерімен шектелген  үш еселі интегралдың интегралдау шектерін
үш еселі интегралдың интегралдау шектерін 
 параметрінің қандай мәндерінде
параметрінің қандай мәндерінде  қатары жинақты?
қатары жинақты?
 функциясының Маклорен қатарына жіктелуін көрсетіңіз
функциясының Маклорен қатарына жіктелуін көрсетіңіз
 функциясының Маклорен қатарына жіктелуін көрсетіңіз
функциясының Маклорен қатарына жіктелуін көрсетіңіз
 функциясының Маклорен қатарына жіктелуін көрсетіңіз
функциясының Маклорен қатарына жіктелуін көрсетіңіз
 функциясының
функциясының 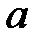 нүктесінде Тейлор қатарына жіктелуін көрсетіңіз
нүктесінде Тейлор қатарына жіктелуін көрсетіңіз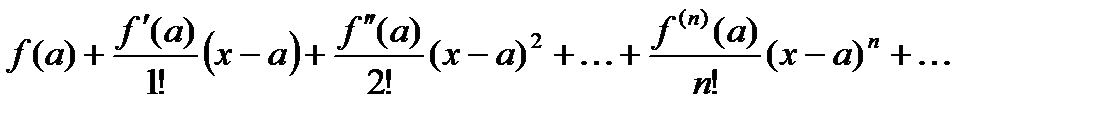
 функциясының дәрежелік қатарға жіктелуін көрсетіңіз
функциясының дәрежелік қатарға жіктелуін көрсетіңіз ,
, 
 қатарының жинақты болу шартын көрсетіңіз
қатарының жинақты болу шартын көрсетіңіз
 дәрежелік қатардың жинақтылық радиусын көрсетіңіз
дәрежелік қатардың жинақтылық радиусын көрсетіңіз
 қатарының шартты жинақты болуының анықтамасы
қатарының шартты жинақты болуының анықтамасы қатар жинақсыз болып, ал
қатар жинақсыз болып, ал  қатар жинақты болса
қатар жинақты болса
 жинақтылық радиусын көрсетіңіз
жинақтылық радиусын көрсетіңіз
 болса, онда
болса, онда 

 болса, онда
болса, онда 

 болса, онда
болса, онда 

 ,
,  болса, онда
болса, онда 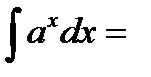

 болса, онда
болса, онда 

 болса, онда
болса, онда 

 - дифференциалданатын функциялар болса, онда
- дифференциалданатын функциялар болса, онда 

 функциясы
функциясы  кесіндісінде интегралданса және
кесіндісінде интегралданса және  теңсіздігі орындалса, онда
теңсіздігі орындалса, онда 

 ,
,  функциялары
функциялары  кесіндісінде интегралданса және
кесіндісінде интегралданса және  , онда
, онда
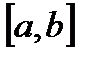 кесіндісінде үзіліссіз болса және
кесіндісінде үзіліссіз болса және 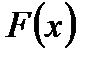 оның қайсыбір алғашқы функциясы болса, онда
оның қайсыбір алғашқы функциясы болса, онда 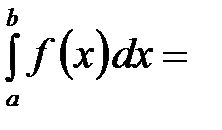



 кесіндісінде параметрлік теңдеумен берілген
кесіндісінде параметрлік теңдеумен берілген  қисығында
қисығында  ,
, 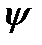 функциялары үзіліссіз болса, онда
функциялары үзіліссіз болса, онда 

 қисығы
қисығы  теңдеуімен берілсе, онда
теңдеуімен берілсе, онда 

 ,
,  теңдеуімен берілсе, онда
теңдеуімен берілсе, онда 

 дифференциалдық теңдеуі үшін
дифференциалдық теңдеуі үшін  шарты орындалса, онда бұл теңдеуді қандай теңдеу деп атайды?
шарты орындалса, онда бұл теңдеуді қандай теңдеу деп атайды? , біртекті, сызықты, тұрақты коэффициентті дифференциалдық теңдеудің сипаттамалық түбірлері нақты болып және
, біртекті, сызықты, тұрақты коэффициентті дифференциалдық теңдеудің сипаттамалық түбірлері нақты болып және  болса, онда жалпы шешім қандай түрде беріледі:
болса, онда жалпы шешім қандай түрде беріледі:
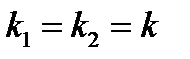 болса, онда жалпы шешім қандай түрде жазылады?
болса, онда жалпы шешім қандай түрде жазылады?
 комплекс сандар болса, онда жалпы шешім қандай түрде жазылады?
комплекс сандар болса, онда жалпы шешім қандай түрде жазылады?
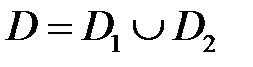 , мұндағы
, мұндағы  және
және  аймақтарының шекаралары ортақ, онда
аймақтарының шекаралары ортақ, онда 


 болса, онда
болса, онда 

 функциясы
функциясы  аймағында үзіліссіз болса, онда
аймағында үзіліссіз болса, онда  екі еселі интеграл нені білдіреді?
екі еселі интеграл нені білдіреді?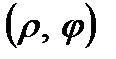 полярлық координаталардан
полярлық координаталардан  тік бұрышты координаталарға көшу үшін қандай формула қолданылады?
тік бұрышты координаталарға көшу үшін қандай формула қолданылады?
 облысы
облысы  ,
,  , мұндағы
, мұндағы  , қисықтарымен шектелген және
, қисықтарымен шектелген және  функциялары
функциялары  кесіндісінде үзіліссіз болса, онда
кесіндісінде үзіліссіз болса, онда 

 ,
,  , мұндағы
, мұндағы  қисықтарымен шектелген және
қисықтарымен шектелген және  функциялары
функциялары  кесіндісінде үзіліссіз болса, онда
кесіндісінде үзіліссіз болса, онда 

 , онда
, онда 

 тік бұрышты параллелипипед болса, онда
тік бұрышты параллелипипед болса, онда 

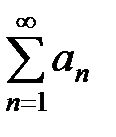 жинақты болса, онда
жинақты болса, онда
 және
және  қатарларының
қатарларының  мүшелері үшін
мүшелері үшін  теңсіздіктер орындалса, онда
теңсіздіктер орындалса, онда қатарының жинақтылығынан
қатарының жинақтылығынан  қатардың жинақтылығы шығады
қатардың жинақтылығы шығады болса, онда
болса, онда  дәрежелік қатарының жинақтылық радиусы неге тең?
дәрежелік қатарының жинақтылық радиусы неге тең?
 дәрежелік қатары нөлге тең емес
дәрежелік қатары нөлге тең емес  нүктесінде жинақты болса, онда
нүктесінде жинақты болса, онда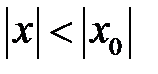 теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық  -тер үшін қатар абсолют жинақты болады
-тер үшін қатар абсолют жинақты болады - қатары
- қатары  нүктесінде жинақсыз болса, онда ол
нүктесінде жинақсыз болса, онда ол теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық  -тер үшін жинақсыз болады
-тер үшін жинақсыз болады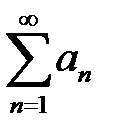 қатары жинақты болса, онда
қатары жинақты болса, онда  қатары туралы не айтуға болады?
қатары туралы не айтуға болады? қатары
қатары  нүктесінде жинақты болса, онда қатар
нүктесінде жинақты болса, онда қатар болғанда әрбір
болғанда әрбір 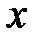 нүктесінде абсолют жинақты
нүктесінде абсолют жинақты







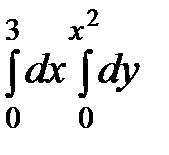











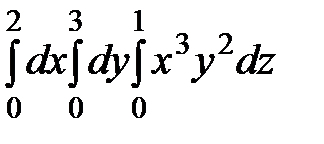



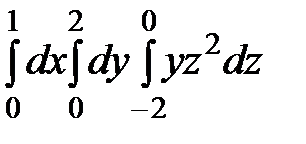

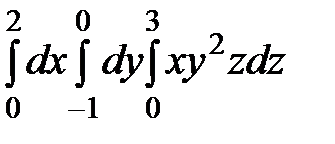






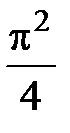







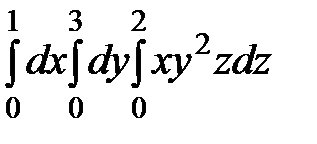




 , (
, (  ) сандық қатары үшін дұрыс тұжырымды көрсетіңіз
) сандық қатары үшін дұрыс тұжырымды көрсетіңіз болса қатар жинақты
болса қатар жинақты сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді:
сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді:


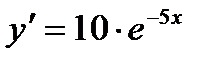






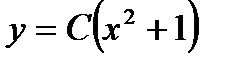
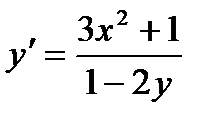














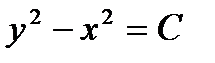










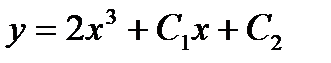
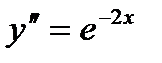



 ,
,