 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение запаса прочности при регулярном нагружении и действии переменных нормальных или касательных напряжений 12
Расчеты на прочность при действии переменных напряжений, или иначе, расчеты на выносливость проводят после определения размеров элементов конструкции по условиям статической прочности. Так как на сопротивление материалов усталости влияют множество трудно учитываемых факторов, то неточности расчета компенсируют, уточняя коэффициенты запаса прочности на основе опыта эксплуатации соответствующих конструктивных элементов. Допускаемые коэффициенты запаса различных деталей одного изделия могут при этом существенно отличаться. Так, например, в авиационных двигателях для диска турбины коэффициент запаса прочности принимают равным 2,2, для лопаток турбины – 3…4, для вала турбины 1,5…3,0. Оценку прочности проводят путем сопоставления расчетного коэффициента запаса прочности n с допускаемым коэффициентом запаса прочности – [n], т.е. по соотношению Рассмотрим порядок определения коэффициента запаса прочности детали по нормальным напряжениям при регулярном нагружении, заданном амплитудой
Предположим, что среднее значение
Рис. 17.3. Определение предельной амплитуды цикла
На рис.17.3 зависимости (17.13) соответствует кривая 2, заданному уровню нагруженности - точка А. Предположим, что предельное состояние, соответствующее циклической долговечности N0, достигается путем одновременного увеличения параметров цикла напряжений (амплитуды
Отсюда, убирая индекс 1 у амплитуды и среднего значения нагружения (т.е. рассматриваем задачу в общем случае), для коэффициента запаса прочности получаем:
В некоторых случаях предельное состояние достигается только за счет увеличения амплитуды напряжений (отрезок АС). Например, амплитуда напряжений в стержне рамы крепления двигателя может изменять по мере изменения его оборотов, а средние напряжения, определяемые силой тяжести двигателя, остаются неизменными. Подобное нагружение реализуется в барабанах колес опор шасси ЛА. В таком случае имеем:
Тогда
При переменных касательных напряжениях формулы для коэффициентов запаса имеют тот же вид, только в зависимостях (17.14 – 17.16) символ σ необходимо заменить на τ.
12 |
.
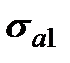и средним напряжением 
. Предельная амплитуда может быть определена по диаграмме предельных амплитуд. На рис. 17.3 прямая 1 соответствует диаграмме предельных амплитуд лабораторных образцов и определяется зависимостью:
мало влияет на чувствительность материалов к конструктивным, технологическим и эксплуатационным факторам, рассмотренным ранее в связи с их влиянием на предел выносливости. В этом случае при любом среднем напряжении цикла предельную амплитуду детали можно определить по зависимости:
(17.13)
и среднего значения 
) в 
раз (точка В на рис. 17.3). Такое положение имеет место, например, при моделировании нагруженности элементов конструкции крыла самолета при увеличении скорости полета. Так как точка В лежит на прямой 2, то координаты этой точки должны удовлетворять уравнению (17.13). Получаем:
(17.14)
(17.15)