 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Экзаменационная работа 10 класс.
Экзаменационная работа 10 класс. Вариант №1 Часть1 В1.Упростите выражение: 2sin2x+4+2cos2x. B2.Решите уравнение: 2cosx-1=0 В3.Найдите значение производной функции:у=2cos3x-12 в точке х0=0. В4. При каких значениях х выполняется равенство f/(x)=5, если известно, что f(x)=4 В5.Упростите выражение: ctg2x(1-cos2x), если cosx=0,2. В6.Упростите выражение: 4sin3α∙cos4α+sin(π+α)-4sin4α∙cos3α. В7.Найдите значение производной функции y=x2∙sinxв точке х0= В8. Решите уравнение: cos22x+3cos2x+2=0. В9. Составьте уравнение касательной к графику функции у= В10.Функция у=f(x) определена на промежутке (c;d). На рисунке изображен график производной функции у=f/(x). Найдите число точек минимума функции у=f(x).
В11. В правильной треугольной пирамиде SАВС т. М-середина ребра АВ, S-вершина. Известно, что SМ=12, а площадь боковой поверхности равна 108. Найдите длину отрезка ВС.
Часть 2 С1.Вычислите С2. Точка движется покоординатной прямой согласно закону х(t)=t3+t2+2, где х(t) координаты точки в момент времени t. В какой момент времени ускорение точки будет равно 8 м/с2? С3. Найдите максимум функции у= С4.Решите уравнение: С5.В прямоугольном параллелепипеде АВСDА1В1С1D1 АВ=2, А =АА1=1.Найдите угол между прямой АВ1 и плоскостью АВС1.
Экзаменационная работа 10 класс. Вариант №2 Часть1 В1.Упростите выражение: 2sin2x+2sin2x∙ctg2x. B2.Решите уравнение: 5sinx=0 В3.Найдите скорость изменения функции: y=2cos(2x-2)-2x в точке х0=1. В4. При каких значениях х выполняется равенство f/(x)=-3, если известно, что f(x)=15-2х+4 В5.Упростите выражение: 5+2ctg2x∙sin2x, если cos2x=0,3. В6.Упростите выражение: В7.Найдите значение производной функции y= В8. Решите уравнение: sin2 В9. Составьте уравнение касательной к графику функции у=tgx в точке с абсциссой х0= В10.Функция у=f(x) определена на промежутке (a;b). На рисунке изображен график производной функции у=f/(x). Найдите количество промежутков убывания функции у=f(x).
В11. В правильной треугольной пирамиде SАВС т.Q-середина ребра АВ, S-вершина. Известно, что ВС =7, а площадь боковой поверхности равна 294. Найдите длину отрезка SQ.
Часть 2 С1.Вычислите С2. Точка движется покоординатной прямой согласно закону s(t)=-9t2+t3-11, где s(t) – координата точки в момент времени t (t –время движения в секундах). При этом тело движется до тех пор, пока его ускорение не обратится в нуль. Сколько секунд, считая от момента времени t=0, находится тело в движении? С3.Найдите минимум функции С4.Решите уравнение: С5.В правильной шестиугольной призме АВСDEFА1В1С1D1Е1F1все ребра равны 1. Найдите расстояние от точки В до плоскости DЕА1.
Экзаменационная работа 10 класс. Вариант №3 Часть1 В1.Упростите выражение: 1-cos2x+tg2x∙cos2x. B2.Решите уравнение: sinx+ sin2x+cos2x=0. В3.Найдите значение производной функции: у=5-2х+sin В4. При каких значениях х выполняется равенство f/(x)=11, если известно, что f(x)= В5.Упростите выражение: 3tg2x∙cos2x-5, если sinx=0,4. В6.Упростите выражение: В7.Найдите значение производной функции В8. Решите уравнение: cos10x+2sin25x=2sinx. В9. Определите абсциссу точки, в которой касательная к графику функции у=-4х+2 В10. Функция у=f(x) определена на промежутке (a;b). На рисунке изображен график производной функции у=f/(x). Найдите количество промежутков убывания функции у=f(x).
В11. В правильной треугольной пирамиде SАВС т.M-середина ребра AВ, S-вершина. Известно, что BC =4, а площадь боковой поверхности равна 174. Найдите длину отрезка SM .
Часть 2 С1.Вычислите С2. Тело движется покоординатной прямой согласно закону х(t)=t3-5t2+6t+7, где х(t) координаты точки в момент времени t. В какой момент времени ускорение точки будет равно 8 м/с2? С3. Найдите минимум функции C4.Решите уравнение: С5. В прямоугольном параллелепипеде АВСDА1В1С1D1 АВ=2, АD =AA1 =1. Найдите угол между прямой АВ1 и плоскостью АВС1.
Экзаменационная работа 10 класс. Вариант №4 Часть1 В1.Упростите выражение: B2.Решите уравнение: В3.Найдите скорость изменения функции: y=sin4x-5x в точке х0=0. В4. При каком наименьшем значениих выполняется равенство f/(x)= 0, если известно, что В5.Упростите выражение: ctg2x-2cos2x∙tg2x, если sin2x= В6.Упростите выражение: В7.Найдите значение производной функции y=(5х+4)2∙sinx в точке х0=0. В8. Решите уравнение: cos3x+sin2x∙cosx= В9. Составьте уравнение касательной к графику функции у=ctg В10.Функция у=f(x) определена на промежутке (-6;3). На рисунке изображен график производной функции у=f/(x). Укажите точку максимума функции у=f(x).
В11. В правильной треугольной пирамиде SАВС т.N-середина ребра ВC, S-вершина. Известно, что SN =6, а площадь боковой поверхности равна 54. Найдите длину отрезка AB.
Часть 2 С1.Вычислите С2.Два тело совершают прямолинейное движение по законам s1(t)=3t2-2t+10, s2(t)=t2+5t+1, где t- время в секундах, а s1(t) и s2(t) – пути в метрах, пройденные соответственно первым и вторым телами. Через сколько секунд, считая от t=0, скорость движения первого тела будет в два раза больше скорости движения второго тела? С3. Найдите длину промежутка возрастания функции у=- С4.Решите уравнение: С5.В правильной шестиугольной призме АВСDEFА1В1С1D1Е1F1все ребра равны 1. Найдите расстояние от точки В до плоскости DЕА1.
Пояснительная записка Данная экзаменационная работа составлена для 10-х классов по курсу «Алгебра и начала анализа. Геометрия. 10 класс» (учебник А.Г.Мордкович, ). Работа представлена в виде теста, состоящего из двух частей и содержит всего16заданий разного уровня. На выполнение работы отводится 2 часа (120 минут). Часть1 содержит 11 заданий базового уровня. К каждому заданию В1-В11 надо дать краткий ответ. В11-геометрическая задача по теме «Многогранники» (уровня В8 ЕГЭ-2012). Часть 2 содержит 5 более сложных заданий. При их выполнении надо записать подробное обоснованное решение. С5- геометрическая задача (уровня С2 ЕГЭ). За выполнение каждого задания обучающийся получает определенное число баллов. В1-В11- по 1 баллу. С1-С5- по 2 балла. Всего- 21 балл. Таблица перевода тестовых баллов в оценки.
Ответы к тестам
|



 ?
? .
. в точке с абсциссой х0=π.
в точке с абсциссой х0=π.
 х3-4х2+15х-15.
х3-4х2+15х-15.
 ?
? .
. в точке х0=0.
в точке х0=0.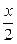 -5sin
-5sin  .
.
 .
. .
. ?
?
 в точке
в точке  .
. образует с положительным направлением оси абсцисс угол в 450.
образует с положительным направлением оси абсцисс угол в 450.
 .
. =0.
=0.
 ctgx=0.
ctgx=0. ?
? .
.
 cos2x.
cos2x. .
.
 =0.
=0.