 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Закон сохранения и превращения энергии
Законы сохранения в механике 1. Энергия, работа, мощность 2. Кинетическая энергия 3. Потенциальная энергия 4. Закон сохранения и превращения энергии 5. Закон сохранения импульса
Энергия, работа, мощность Изменение механического движения тела вызывается силами, которые действуют на него со стороны других тел. С целью количественно описать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила F, составляющая некоторый угол α с направлением перемещения, то работа этой силы равна:
Если взять участок траектории от точки 1 до точки 2, то работа на нем равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Единица работы - джоуль (Дж): 1 Дж - работа, совершаемая силой 1 Н на пути 1 м. Работу считают положительной, если вектор силы совпадает с направлением движения, и отрицательной при векторе силы, направленном в противоположную движению сторону. Примером отрицательной работы может быть действие тормозящей силы. Мощность –это работа, совершенная за единицу времени
Единица мощности – ватт (Вт). С работой и мощностью связано понятие о механической энергии. Механическая энергия — это особая физическая величина, характеризующая способность тел совершать работу. Эквивалентность работы и энергии дает основание измерять эти величины в одинаковых единицах Энергия - универсальная мера различных форм движения и взаимодействия. В механике различают два вида энергии: кинетическую и потенциальную.
Кинетическая энергия Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от v1 до v2, то силы совершили определенную работу A. Пусть тело движется вдоль прямой линии под действием постоянной силы
Отсюда, с учетом 2 закона Ньютона, следует, что
Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости). Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Кинетическая энергия – это энергия движения, поэтому она всегда положительна и зависит от выбора системы отсчета Единица кинетической энергии та же, что и единица работы- джоуль (Дж). Потенциальная энергия Потенциальная энергия -энергия взаимодействия тел. Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными. Работа консервативных сил на замкнутой траектории равна нулю. Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии. Физическая величина называется потенциальной энергией тела в поле силы тяжести Eр = mgh. Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком A = –(Eр2 – Eр1). Потенциальная энергия Eр зависит от выбора нулевого уровня. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔEр = Eр2 – Eр1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня. Понятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину Ер= (kx2)/2 Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости.
Закон сохранения и превращения энергии Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком, эта же работа определяется и по теореме о кинетической энергии, следовательно: Ek1 + Ep1 = Ek2 + Ep2. Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему консервативных сил, остается неизменной. Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.
Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами. Сила трения не является консервативной. Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии. Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии. Закон сохранения импульса При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.
Механические колебания 1. Гармонические колебания. 2. Маятники. Гармонические колебания Колебанияминазываются процессы, в той или иной степени, повторяющиеся во времени. Изменение координаты точки при колебании можно описать уравнением X(t) = A cos(wt+ Движение, при котором координата точки изменяется по закону косинуса (или синуса) называетсягармоническим колебанием. Гармоническое колебание точки определяется тремя параметрами: А, w и φ0. Параметр A называется амплитудой колебаний, он равен максимальному отклонению точки от центрального положения (положения равновесия). Эта величина имеет ту же размерность, что и координата x, то есть размерность длины. Изменяющаяся величина Параметр ω называется круговой(циклической) частотой колебаний. Время одного колебания T называется периодом колебаний. Круговая частота связана с периодом колебания соотношением
Если период – это время одного колебания, то величина обратная периоду равна числу колебаний в единицу времени, то есть частоте колебаний
Связь круговой (циклической) и обычной частоты колебаний
Маятники Маятник - тело, совершающее под действием переменной силы колебания. 1. Пружинный маятник — это груз массой m, который подвешен на пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Пружинный маятник совершает гармонические колебания по закону х = А соs (ω0t+φ) с циклической частотой
и периодом
2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела. Циклическая частота
При малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом
где введена величина L=J/(ml) — приведенная длина физического маятника. 3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то найдем выражение для периода малых колебаний математического маятника
|





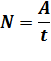
 , при этом тело переместилось на
, при этом тело переместилось на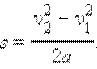




 ).
). называется фазой колебания, а величина φ0 - начальной фазой.
называется фазой колебания, а величина φ0 - начальной фазой. .
.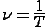 .
. .
.

 ,
, ,
,