 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задания для самостоятельного решения
Кратные интегралы Занятие №1 1. Двойной интеграл Пусть функция f(x;y) определена в замкнутой ограниченной области (D)ÌR2. Разобьем эту область на частичные области (D1), (D2),¼, (Dn), площади которых равны DS1, DS2,¼, DSn соответственно. Обозначим через dk диаметр области (Dk): dk = sup{|M¢M²|; M¢,M²Î(Dk)}. Число
При этом говорят, что f(x;y) интегрируема в (D). Для интегрируемости f(x;y) в ограниченной замкнутой области (D) достаточно, чтобы f(x;y) была непрерывна в (D). Теорема 1. Если f(x;y), g(x;y) интегрируемы в (D), то k1f(x;y)+k2g(x;y) также интегрируема в (D) и при этом
Теорема 2. Если f(x;y) интегрируема в области (D),
Правая часть последнего равенства обычно записывается иначе:
В случае, если область (D) имеет сложный вид, то ее разбивают на простые подобласти и применяют теорему 2. 2. Приложения двойного интеграла Вычисление площадей плоских фигур. В декартовой прямоугольной системе координат площадь S плоской фигуры (D) выражается интегралом
Вычисление объемов тел. Объем V цилиндрического тела (T), ограниченного сверху поверхностью z = f(x;y), снизу – плоскостью
где (D) – проекция тела (T) на координатную плоскость Оxy. Площадь поверхности.Если в пространстве с заданной прямоугольной системой координат гладкая поверхность (W) задана уравнением
Механические приложения. Пусть имеется плоская пластина, занимающая область (D) плоскости 0xy и имеющая поверхностную плотность g(x;y). Тогда масса М этой пластины вычисляется по формуле
а координаты ее центра тяжести – по формулам
Статические моменты Мx, Мy пластины относительно осей Оx и Оy вычисляются по формулам
а моменты инерции
Момент инерции I0 пластины относительно начала координат равен I0 =
Если g º 1 (пластина однородная и ее плотность всюду равна 1), то в формулах моменты называются геометрическими моментами. 3. Тройной интеграл Пусть непрерывная функция
называется интегральной суммой функции f(x;y;z) по области (Т). Число Свойства тройного интеграла аналогичны свойствам двойного интеграла. Вычисление тройного интеграла сводится к вычислению повторного интеграла. Если область (Т) ограничена снизу поверхностью z = j1(x;y), сверху – поверхностью z = j2(x;y), с боков – цилиндрической поверхностью с образующей, параллельной оси Оz, и (D) – проекция тела (Т) на координатную плоскость Оxy, то
Задачи Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения, теоремы и понятия. 1.Записать двойной интеграл 1) Ответ. 2) Ответ. 3) Ответ. 4)
Ответ. 5)
Ответ.
2.Изменить порядок интегрирования в повторном интеграле:
1) Ответ. 2) Ответ. 3) Ответ. 3.Вычислить двойной интеграл: 1) Ответ. 2) Ответ. 4.Найти площадь фигуры, ограниченной линиями: Ответ. 5.Вычислить тройной интеграл 1) Ответ. 2) Ответ. 6.Вычислить с помощью тройного интеграла объем тела V, ограниченного поверхностями: Ответ.
5. Задания для самостоятельного решения: 1.Записать двойной интеграл 1) Ответ. 2) Ответ. 3) Ответ. 4) Ответ. 5) Ответ. 6) Ответ. 7) Ответ. 8) Ответ. 2.Изменить порядок интегрирования в повторном интеграле: 1) Ответ. 2) Ответ. 3) Ответ. 4) Ответ. 3.Вычислить двойной интеграл: 1) Ответ. 2) Ответ. 3) Ответ. 4. 4) Ответ. -4.
4.Вычислить тройной интеграл от заданной функции по области (V), ограниченной указанными поверхностями: 1) Ответ. 2) Ответ. 3) Ответ. 4) Ответ. 4.
5) Ответ. 6) Ответ. 2. 7) Ответ. 8. 8) Ответ. 2. 9) Ответ. 1. 10) Ответ. 4. 11) Ответ. 1. 12) Ответ. 2. 13) Ответ. 3. 5.Вычислить с помощью тройного интеграла объем тела V, ограниченного поверхностями: Ответ.
Занятие №2
1. Замена переменных в двойном интеграле Пусть система уравнений
осуществляет взаимно-однозначное соответствие между областью (D) плоскости Оxy и областью (G) плоскости Оuv, пусть при этом функции x(u,v), y(u,v) непрерывно дифференцируемы и якобиан
Этой формулой пользуются в тех случаях, когда область (G) имеет более простую форму, чем (D). В частности, при переходе в полярную систему координат
и
2. Замена переменных в тройном интеграле Тройной интеграл
В цилиндрической системе координат каждой точке М пространства с заданной декартовой прямоугольной системой координат ставится в соответствие упорядоченная тройка чисел
Якобиан перехода равен J = r. При этом
(Часто вместо z¢ пишут просто z).
Уравнение r = c, c ³ 0 задает сферу радиуса c (чем и объясняется название системы координат),
Якобиан перехода J = r2sinq. В новой системе координат
Задачи Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения и понятия: 1.Записать двойной интеграл 1) Ответ. 2) Ответ. 3) Ответ. 4) Ответ. 5) Ответ. 6) Ответ. 7) Ответ. 8) Ответ.
2.Вычислить двойной интеграл, переходя к полярным координатам: 1) Ответ. 2) Ответ. 3) Ответ. 3.В тройном интеграле 1) Ответ. 2) Ответ.
3) Ответ.
4) Ответ. 5) Ответ. 6) Ответ. 7) Ответ. 4.В тройном интеграле 1) Ответ.
2) Ответ. 3) Ответ. 4) Ответ. 5) Ответ. 6) Ответ. 5.Вычислить тройной интеграл в цилиндрической или сферической системе координат: 1) Ответ.
2) Ответ. 3) Ответ. 4) Ответ.
6.Вычислить объем тела V (в цилиндрической или сферической системе координат): 1) Ответ.
2) Ответ.
Задания для самостоятельного решения 1.Вычислить тройной интеграл в цилиндрической или сферической системе координат: 1) Ответ. 2) Ответ.
3) Ответ.
4) Ответ.
5) Ответ.
6) Ответ.
7) Ответ. 0.
8) Ответ.
9) Ответ.
10) Ответ.
2.Вычислить объем тела V (в цилиндрической или сферической системе координат): 1) Ответ. 2) Ответ. 3) Ответ. 4) Ответ.
|



 называется диаметром разбиения. В каждой частичной области (Dk) возьмем по точке Мk(xk;yk). Выражение
называется диаметром разбиения. В каждой частичной области (Dk) возьмем по точке Мk(xk;yk). Выражение  называется интегральной суммой функции f(x;y) по области (D). Если существует конечный предел интегральных сумм G при l®0, предел, не зависящий ни от способа разбиения, ни от выбора точек Мk, то этот предел называется двойным интегралом от функции f(x;y) по области (D) и обозначается
называется интегральной суммой функции f(x;y) по области (D). Если существует конечный предел интегральных сумм G при l®0, предел, не зависящий ни от способа разбиения, ни от выбора точек Мk, то этот предел называется двойным интегралом от функции f(x;y) по области (D) и обозначается  :
: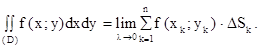
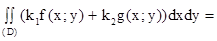
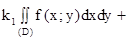

 и пусть площадь множества
и пусть площадь множества  равна нулю. Тогда
равна нулю. Тогда
 Вычисление двойного интеграла сводится к вычислению повторного интеграла. Если f(x;y) непрерывна в замкнутой области (D) и (D) ограничена непрерывными линиями y = j(x), y = y(x), x = а, x = b, j(x)£y(x) при а £ x £ b, то
Вычисление двойного интеграла сводится к вычислению повторного интеграла. Если f(x;y) непрерывна в замкнутой области (D) и (D) ограничена непрерывными линиями y = j(x), y = y(x), x = а, x = b, j(x)£y(x) при а £ x £ b, то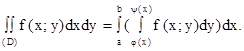

 Иногда удобно производить внешнее интегрирование по y, внутреннее – по x: если (D) ограничена линиями x = j(y), x = y(y), y = c, y = d, j(y) £ y(y) при y Î[c,d], то
Иногда удобно производить внешнее интегрирование по y, внутреннее – по x: если (D) ограничена линиями x = j(y), x = y(y), y = c, y = d, j(y) £ y(y) при y Î[c,d], то

 , с боков – цилиндрической поверхностью с образующими, параллельными оси 0z, выражается двойным интегралом
, с боков – цилиндрической поверхностью с образующими, параллельными оси 0z, выражается двойным интегралом
 и (D) – проекция этой поверхности на координатную плоскость Оxy, то площадь S этой поверхности выражается формулой
и (D) – проекция этой поверхности на координатную плоскость Оxy, то площадь S этой поверхности выражается формулой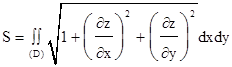 .
.




 пластины относительно осей Оx и Оy выражаются формулами
пластины относительно осей Оx и Оy выражаются формулами

 . Центробежный момент
. Центробежный момент  пластины рассчитывается по формуле
пластины рассчитывается по формуле
 определена в замкнутой, ограниченной области (Т) Ì R3. Разобьем (Т) на частичные подобласти (Тк), 1£ k £ n, обозначим через dk диаметр (Тk):
определена в замкнутой, ограниченной области (Т) Ì R3. Разобьем (Т) на частичные подобласти (Тк), 1£ k £ n, обозначим через dk диаметр (Тk):  через DVk – объем (Тk). В каждой частичной области (Тк) выберем по точке Mк(xk;yk;zk). Выражение
через DVk – объем (Тk). В каждой частичной области (Тк) выберем по точке Mк(xk;yk;zk). Выражение
 называется диаметром разбиения. Если существует предел интегральных сумм при
называется диаметром разбиения. Если существует предел интегральных сумм при  (предел, не зависящий ни от способа разбиения (Т), ни от выбора точек Mк), то этот предел называется тройным интегралом функции u = f(x;y;z) по области (Т) и обозначается
(предел, не зависящий ни от способа разбиения (Т), ни от выбора точек Mк), то этот предел называется тройным интегралом функции u = f(x;y;z) по области (Т) и обозначается 


 в виде повторных интегралов двумя способами, если задана область D:
в виде повторных интегралов двумя способами, если задана область D:
 .
.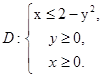
 .
.
 .
.
 .
.


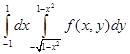 .
. .
. .
. .
. .
. .
.
 .
.
 .
.
 .
. от заданной функции
от заданной функции  по области (V), ограниченной указанными поверхностями:
по области (V), ограниченной указанными поверхностями: ,
, 
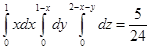 .
. ,
, 
 .
.
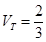 .
.
 .
.
 .
.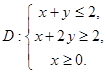
 .
.
 .
.
 .
.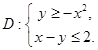
 .
.
 .
.
 .
. .
. .
. .
. .
.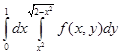 .
. .
. .
.
 .
.
 .
.

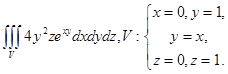
 .
.
 .
.
 .
.

 .
.





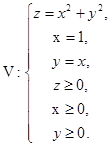
 .
.
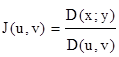 отличен от 0 во всех точках области G. Тогда имеет место формула замены переменных в двойном интеграле
отличен от 0 во всех точках области G. Тогда имеет место формула замены переменных в двойном интеграле
 J(u;v) = r
J(u;v) = r
 иногда проще вычислить, если перейти к новой системе координат Оuvw. Если замена переменных происходит с помощью функций
иногда проще вычислить, если перейти к новой системе координат Оuvw. Если замена переменных происходит с помощью функций  ,
,  ,
,  и эти функции осуществляют взаимно-однозначное соответствие между областью (Т) в системе Оxyz и областью (Т1) в системе О1uvw и якобиан
и эти функции осуществляют взаимно-однозначное соответствие между областью (Т) в системе Оxyz и областью (Т1) в системе О1uvw и якобиан  непрерывен и не обращается в нуль, то справедлива формула
непрерывен и не обращается в нуль, то справедлива формула

 Наиболее употребительными из криволинейных координат являются цилиндрические и сферические системы координат.
Наиболее употребительными из криволинейных координат являются цилиндрические и сферические системы координат. – длина вектора
– длина вектора  , где М¢ – проекция точки М на плоскость 0xy, j – угол между вектором
, где М¢ – проекция точки М на плоскость 0xy, j – угол между вектором  , 0 £ j < 2p (или –p £ j < p), –¥ < z¢ < +¥. Уравнение r = с, где с – константа, с ³ 0, задает цилиндр в пространстве, уравнение j = с задает полуплоскость, z¢ = c – плоскость. Переход к цилиндрической системе координат осуществляется с помощью формул
, 0 £ j < 2p (или –p £ j < p), –¥ < z¢ < +¥. Уравнение r = с, где с – константа, с ³ 0, задает цилиндр в пространстве, уравнение j = с задает полуплоскость, z¢ = c – плоскость. Переход к цилиндрической системе координат осуществляется с помощью формул


 В сферической системе координат каждой точке М(x;y;z) пространства с заданной декартовой прямоугольной системой координат ставится в соответствие упорядоченная тройка чисел (r, q, j) – сферические координаты, где r – длина вектора
В сферической системе координат каждой точке М(x;y;z) пространства с заданной декартовой прямоугольной системой координат ставится в соответствие упорядоченная тройка чисел (r, q, j) – сферические координаты, где r – длина вектора  q – угол между вектором
q – угол между вектором  и положительным направлением оси Оz,
и положительным направлением оси Оz, 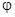 – угол между вектором
– угол между вектором  – однополостный круговой конус, j = c – полуплоскость. Формулы перехода к сферической системе координат имеют вид
– однополостный круговой конус, j = c – полуплоскость. Формулы перехода к сферической системе координат имеют вид






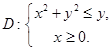



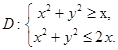






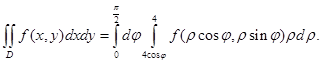
 ,
, 
 .
. ,
, 
 .
. ,
, 
 .
.


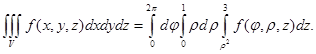














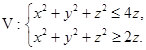








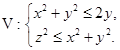



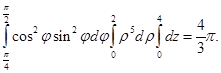







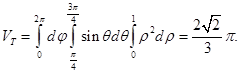


 ,
, 
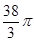 .
.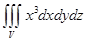 ,
, 
 .
.
 .
. ,
, 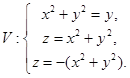
 .
. ,
, 
 .
. ,
, 
 .
. ,
, 
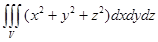 ,
, 
 .
.
 .
. ,
, 
 .
.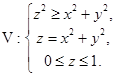
 .
.
 .
.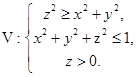
 .
.
 .
.