 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Взаимно обратные числа и их сумма.
Любое рациональное число можно представить в виде конечной или бесконечной периодическое десятичной дроби. Иррациональные числа – бесконечные непериодические дроби. Обозначение I. Действительные числа – множество рациональных и иррациональных чисел. Обозначение R.
Периодическая десятичная дробь – десятичная дробь называется периодической, если с некоторого разряда начинается повторение одной цифры или группы цифр. Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь — бесконечной десятичной периодической дробью. Любую конечную или бесконечную периодическую десятичную дробь можно представить в виде обыкновенной Дроби. Перевод в обыкновенную дробь Пусть x=1,(47) 100x=147,474747... . Следовательно, _ 100x=147,(47) x=1,(47) _________________________________ 100x−x=147,(47 )−1,(47) 99x=146 x= Итак, 1,(47)= x=1,3(47 ). Сначала умножим x на 10, чтобы в полученном произведении период начинался сразу после запятой: 10x=13,(47) . Число 10x умножим на 100 — тогда запятая сместится ровно на один период вправо: 1000x=1347,(47) Имеем: _1000x=1347,(47) 10x=13,(47) __________________________ 990x=1334; X = Приближения
До десятых До сотых 2) Решение квадратных неравенств. Если в левой части неравенства стоит квадратный трехчлен, а в правой - ноль, то такое неравенство называется квадратным. Например, неравенства 2х2 + 3х - 1 ≥ 0, -3х2 +4х +5 ≤ 0 являются квадратными. Решением неравенства с одним неизвестным называется то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство. Решить неравенство - это значит найти все его решения или установить, что их нет. Способы решения. Системный Для решения неравенства этим способом нужно: 1) определить корни соответствующего квадратного уравнения; 2) разложить неравенство на множители; 3) составить и решить две системы линейных неравенств. х2 - 5х + 6 ≥ 0. Решение: Квадратное уравнение х2 – 5х + 6 = 0 имеет два корня х = 2, х = 3. Следовательно, левую часть неравенства можно разложить на множители и записать так: (х - 2)(х - 3) ≥ 0. 1 2 Итак, все числа х ≥ 3, а также числа х ≤ 2 являются решениями неравенства (х - 2)(х - 3) ≥ 0, а значит и исходного неравенства х2 - 5х + 6 ≥ 0. Ответ: х ≤ 2, х ≥ 3. Графический способ решения 1) определить направление ветвей параболы по знаку первого коэффициента; 2) найти действительные корни соответствующего квадратного уравнения или установить, что их нет; 3) Построить эскиз графика и по нему определить промежутки, где функция принимает нужные значения.
Метод интервалов.
При х = -3, х = -2 Ответ: -3<x<-2

Билет №3. Пропорции. Свойства. Решение пропорций. Прямая и обратная пропорциональности, их графики. Неполные квадратные уравнения
?!?!Серяпин -
Билет №4. Проценты. Три типа задач. Формулы сокращённого умножения. Арифметический корень натуральной степени. Функция I. 1.Процеты Определение. Процентом числа называется его сотая часть. Пример. 1% = 2. Перевод из процентов в дробь 2.1) В десятичную дробь Чтобы перевести процент в десятичную дробь нужно убрать знак % и разделить на 100 2.2) Перевод дроби в процент Чтобы перевести дробь в % нужно число умножить на 100 и поставить знак % 2.3) Перевод обыкновенной дроби в % Нужно перевести её в десятичную и выполнить (2.2) II. Три типа задач 1. Процент от числа Задача 1 Найти указанный процент от заданного числа Решение Число a умножится на указанное число процентов p, а затем произведение делится на 100
a- заданное число p- указанный процент 2. Число по процентам Задача 2. Найти число по заданной части b выраженной в процентах p. Решение. Заданная часть b делится на кол-во процентов p и умножается на 100
3. Процентное отношение Задача 3. Найти в % выражение одного числа b от другого числа a Решение Первое число b делится на второе a и результат умножается на 100
(здесь должна быть маленькая табл, у меня её нет(((
2 вопрос Арифметический корень из натуральной степени А.к.н.с. n≥2 из неотрицательного числа а называют некоторое число, n-я (нная) степень которого равна а
· Корень нечетной степени из отрицательного числа Задача 2 (стр 44)
· Свойства Если 1) 2) 3) 4)
· При n=2 (четная) При любом n- четном, функция имеет 1 вид(чем больше n тем график больше прижимается к оси оу) и одни свойства. При n=3 (нечетная)

Билет №5. Т. Виета и обратная ей. Теорема о корнях 2 . Степень с целым отрицательным показателем. Функция у = х -n , nÎN Теорема Виета: Если х₁ и х₂- корни уравнения х²+рх+q, то справедливы формулы: 1.х₁+х₂=-р 2. х₁*х₂=q х₁= Док-во: 1. х₁+х₂= 2. х₁*х₂=( Теорема обратная теореме Виета: Если числа p,q,х₁, х₂- таковы, что х₁+х₂=-р, а . х₁*х₂=q, то х₁ и х₂- корни уравнения х²+рх+q=0. Док-во: х²+рх+q=0 х²+рх+q=х²-( х₁+х₂)х+( х₁*х₂)=х²-хх₁-хх₂+х₁х₂=х(х-х₂)-х₁(х-х₂)=(х-х₁)(х-х₂) х²+рх+q=0 ; х²+рх+q=(х-х₁)(х-х₂) => (х-х₁)(х-х₂)=0 Теорема о корнях: Если числа m n a b c таковы, что m+n=-b, m*n=ac, то Док-во: ax²+bx+c=0/:а х²+ х₁+х₂= Степень с целым отрицательным показателем: Степень некоторого числа а с отрицательным целым показателем, определяется как единица делённая на степень того же числа равным абсолютной величине отрицательного показателя.
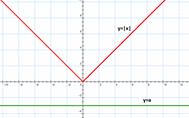
Билет №6. Степень с натуральным показателем. Функция у = х n , nÎN Модуль числа. Определение. Геометрический смысл. Свойства. Функция у = |х| Степень –степенью числа «а» с натуральным показателем «m» больше 1, называется произведение «n» одинаковых множителей, каждый из которых численно равен «а»
a - основание степени, n - показатель степени,
Свойства степеней: 1.При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Доказательство:
2.При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
Доказательство:
3.При возведении степени в степень, показатели перемножаются, а основание остается неизменным.
Доказательство:
4.Чтобы перемножить степени с одинаковыми показателями, достаточно перемножить основания, а показатель степени оставить неизменным. Доказательство:
5.Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным. Доказательство:
Функция у = хп, nÎN. Степенная функция с натуральным показателем, это функция вида Функция у = хп, nÎN.
При n=3 – Кубическая парабола Свойства: 1.D(y): x Є R 2.E(y): y Є R 3.y = 0 при x =0 y < 0 при x < 0 y > 0 при x > 0 4.Возрастающая 5.Нечетная При n – нечетное, функция обладает теми же свойствами, что и функция y = х ³
Билет №7 Функция. Свойства. Простейшие неравенства с модулем (|x|>a); геометрическая интерпретация 1) Основные понятия Опр.- Если каждому числу x из некоторого множества D поставлено в соответствии единственное число y то говорят что на множестве задана функция y=f(x), где x – независимая переменная (аргумент) y – функция (завис. Переменная) f – правило соответствия 1. Опр1- Промежутки знака постоянства. Промежутки знака постоянства называются числовые промежутки, на которых функция принимает только положительные или только отрицательные значения. Опр2- Число a называется нулем функции y=f(x), если f(a)=0. 2. Монотонность Опр.- Функция F(x) называется возрастающей на некотором промежутке x, если большинству значению аргумента соответствует большее значение функции. Опр2- Функция f(x) называется убывающей на некотором промежутке x, если большинству значению аргумента соответствует меньшее значение функции Опр.3- Если функция F(x) является возрастающей или убывающей на некотором промежутке, то она называется монотонной, а сами промежутки промежутками монотонности. 3. Область определения: это множество всех допустимых действительных значений x, при функция y=f(x) определ. Область значения функций – это множество всех действительных значений y, которых принимает функция. 4. Нули функции – Ноль функции такое значение x, при котором значение функции равно нулю. 5. Четность Опр1- Числовое множество x из этого множества число x также принадлежит этому множеству. Опр.2- Функция f(x) называет четной если для любого x выполняется равенство f(-x)=x2-1 График четной функции симметричной относительно оси OY Опр.3- Функцию f(x), называют не четной если для любого x выполнятся равенство f(x)=x3
2ᵒ a<0 xϵR
|x|>0 x≠0
Билет №8. Уравнение прямой. Линейная функция. Решение простейших уравнений c модулем; геометрическая интерпретация. Линейная функция. Опр.1 Линейной функцией называется функция вида k –угловой коэффициент b- свободный член
График функции y=kx+b получается из графика функции y=kx движения вдоль оси на b единиц вверх, если b>0 и на |b|единиц вниз если b<0. 1. решение простейших уравнений с модулем. уравнение |x|=a 1) a<0 Решить уравнение |x|=0 . где a<0
Билет №9. Приведённое квадратное уравнение. Формула корней. Числовые неравенства. Свойства, действия. 1.Приведённое квадратное уравнение. Опр. Приведенным квадратным уравнением называется уравнение, старший коэффициент которого равен единице. Н-р: x²+5x+6=0 ; x²-x+3=0 Любые квадратное уравнение общего вида можно привести к виду приведенного – разделив обе части на a(старший коэффициент).
Н-р: 2x²-7x+6=0 / :a (2) => Формулы корней. Следует из Найдем корень приведенного квадратного уравнения: x²+px+q=0
Н-р: x²-6x-7=0
x₁=7 x₂=-1 2 . Числовые неравенства. Опр. Неравенство - это математические выражения, соединенные знаками: a>b c>d – неравенства одного знака. a>b c<d – неравенства противоположных знаков. Числовые неравенства - неравенство, в записи которого находятся числа или числовые выражения. Н-р: 2<10 ; 569>125 Двойное неравенства – если одновременно выполняются два условия x>a и x<b, то вместо двух неравенств, можно записать одно двойное неравенство => a<x<b. Двойное неравенство можно изобразить на прямой.
a x b Свойства: o Свойства транзитивности. Теорема 1: Если a>b и b>c ; то a>c Дано: a>b ; b>c => a>c Док-во: a-c=a-b+b-c=(a-b)+(b-c)>0 a-c>0 Н-р: 6>0 ; 0>4 -4<0<6 o Прибавление числа Теорема 2 : Если к обеим частям неравенства прибавить одно и то же число, то знак неравенства не изменится. Дано: a>b c∈R c-любое => a+c>b+c Док-во: (a+c)-(b+c)=a+c-b-c a-b – по условию a>b, то a+c>b+c Следствие: Любое слагаемое можно переносить из одной части в другую изменив знак этого слагаемого на противоположный. Дано: a>b+c Док-во: a-c>b a>b+c /+(-c) a-c>b+c-c (a-c)-b=a-(b=c) >0 o Умножение на число 1)Если умножить обе частим неравенства на одно и то же число, то знак неравенства не изменится. Дано: a>b c>0 ac>bc Док-во: ac-bc=c(a-b) >0 2)Если обе части неравенства умножить на одно и то же отрицательное число, то знак меняется на противоположный. Дано: a>b c<0 ac<bc Док-во: ac-bc=c(a-b) <0 Следствие1: Если обе части неравенства разделить на одно и то же положительное число, то знак неравенства не изменится. Дано: a>b c>0 Док-во: a>b /•
Следствие2: Если обе части неравенства разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный. Дано: 0<a<b, то Док-во: a<b Действия: o Сложение неравенств При сложении неравенств одного знака поучается неравенство того же знака. Дано: a>b c>d a+c>b+d Док-во: (a+c)-(b+d)=a+c-b-d= (a-b)+(c-d) o Умножение неравенств. При умножении неравенств одного знака, при которых левые и правые части положительны, получается неравенство того же знака. Дано: a>b>0 c>d>0 ac>bd Док-во: ac-bd= ac+bc-bc+bd=(ac-bc)+(bc-bd)=c(a-b)+b(c-d) o Возведение в степень. 1)Если a>b>0 и n ∈ N, то a в степени N больше b в степени N; если n-нечетное, то условие b>0 лишнее. 2) Если aˆ>bˆ, где a>0, b>0, n ∈ N, то a больше b; если n-нечетное, то условиеa>0 и b>0 лишнее.
Билет №10. Множества. Основные понятия. Способы задания. Операции над множествами. Числовые множества. Числовые промежутки. Квадратное уравнение. Вывод формулы корней полного квадратного уравнения. Формула корней полного квадратного уравнения со вторым чётным коэффициентом. Дискриминант. Основные понятия множеств 1) Множество - это основное математическое понятие, определения не имеет. Под понятием <множество > подразумевают набор предметов, объектов наделенными общими свойствами. Для записи множества с любыми элементами используются фигурные скобки. Элементы множества можно записывать в любом порядке. 2) Виды множеств: Определение 1– Множество, состоящие из конечного числа элементов, называются конечными. Определение 2- Множество, не является конечным, называются бесконечным. · Обозначение: Ø Например: множество книг в библиотек (конечным) Множество натуральных чисел (бесконечным) Множество пяти метровых людей (пустым) 3) Элементы множеств: · Определение: Предметы, объекты, образующие данное множество, называются его элементами. · Обозначения: Латинские строчные буквы a, b, c, d и т.д. a A – элемент a принадлежит множеству А a ɇ A – элемент a не принадлежит множеству А 4) Определение 1 – Если каждый элемент множества В является элементом множества А, то В называют подмножеством множества А. Определение 2- Два множества А и В называются равными (А = В) если они состоят из одних и тех же элементов то есть каждый элемент множества А является элементом множества В является элементом множества А.
Вопрос 2 Способы задания множеств 1) Множество может быть задано причислением всех его элементов по их названиям (применим для конечных множеств. Например: Множество книг в библиотеке Множество учеников в классе 2) Множество может быть задано общей характеристикой (общими свойствами) элементов данного множества. Применим как для конечных так для бесконечных множеств. Запись: A = ( х I P(х)), где Р(х)- характеризующие свойство Например: Множество рациональных чисел Семейство кошачьих Четырёх угольники Вопрос 3 Операции над множествами: · Объединение- множества А и В называют новое множество состоящее из тех же элементов , которые содержится А или В Обозначение: AUB А=(1,2,3,4) В=(3,4,5) АUВ=(1,2,3,4,5) · Разность- разностью называется множество, которое состоит из тех элементов, которые принадлежат множеству А, но не принадлежат множеству В. Обозначение: А\В А=(1,2,3,4) В=(3,4,5) А\В=(1,2,5) · Перечисление: Причислением множеств А и В называют новое множество состоящие из тех объектов которых принадлежат множеству В и А одновременно Обозначение: А∩В Пример: А=(1,2,3,4) В=(3,4,5) А∩В=(1,2,3,4,5) Вопрос 4 Числовые множества 1) Определение: множества, элементами которого являются числа, множества называют числовыми. (т.е. подмножество множества R) Например: А=(1,2,3,4) В=(х | х- четное число. 2) Основные множества чисел
R 3) Числовые промежутки Числовыми промежутками называют подмножество действительных чисел вида. · Определение 1 - Отрезком [a;b] называется множество действительных чисел Х, удовлетворяющих неравенству a ≤ x≤b · Определение 2 - Интервалом (a;b) называется множество действительных чисел Х, удовлетворяющих неравенству a<x<b · Определение 3 - Полу интервалом (a;b] или [a;b) называется множество действительных чисел Х, удовлетворяющих неравенству a<x≤b (или x≤b) · Определение 4 - Лучом [-∞, b) или (-∞, b] называется множество действительных чисел х, удовлетворяющих неравенству x≥a (или x ≤b) · Определение 5 - Открытым лучом (a;+∞)или(-∞,b)называется множество действительных чисел Х, удовлетворяющих неравенству х>a или(x<b)
Билет №11. Среднее арифметическое и среднее геометрическое. Неравенство Коши. Взаимно обратные числа и их сумма. Разложение квадратного трёхчлена на множители. 1) Средним арифметическим a и b называется их полу сумма. Неравенство Коши. Ср. арифм. двух неотрицательных чисел не меньше их ср. геом.
Взаимно обратные числа и их сумма. Взаимно обратные числа – это два числа, произведение которых равно 1. Теорема. Модуль суммы взаимно обратных чисел не меньше 2. |




 .
.
 =
=  =1
=1 
 До целых
До целых получаем х ≥ 3.
получаем х ≥ 3. получаем х ≤ 2.
получаем х ≤ 2.

 Определим знаки функции на промежутках (-
Определим знаки функции на промежутках (-  ;-3), (-3;-2), (-2;
;-3), (-3;-2), (-2;  это одна сотая числа.
это одна сотая числа.


 Например:
Например:  =3
=3 2k+1-это натуральное число.
2k+1-это натуральное число.

 - корень нечетной степени из неотр. Числа
- корень нечетной степени из неотр. Числа :
: 
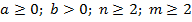 , то
, то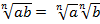


 для док-ва возводим в
для док-ва возводим в 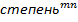



 Вывод: Л.ч. =П.ч.
Вывод: Л.ч. =П.ч. Функция
Функция 



 При любом n- нечетном, функция имеет 1 вид(чем больше n тем график больше прижимается к оси оу) и одни свойства.
При любом n- нечетном, функция имеет 1 вид(чем больше n тем график больше прижимается к оси оу) и одни свойства.
 )²-q х₂=
)²-q х₂=  )²-q
)²-q
 )²-q)=-(
)²-q)=-(  )²-(
)²-(  )²-q)²=((
)²-q)²=(( 
 и
и  –корни уравнения ax²+bx+c=0
–корни уравнения ax²+bx+c=0 x+
x+  =0 х₁+х₂=-
=0 х₁+х₂=-  =-
=-  =
=  =
=  =
= 

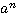 - n-ая степень числа.
- n-ая степень числа.

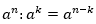






 2) |a|>a
2) |a|>a 1ᵒ a>0
1ᵒ a>0

 3ᵒ a=0
3ᵒ a=0 , где k и b – заданные числа
, где k и b – заданные числа

 Y=0
Y=0 Y=kx
Y=kx 



 Y=kx+b
Y=kx+b

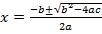
 =-
=-  ±
±  =-
=-  =
=  ±
± 
 ±
± 
 =3±4
=3±4 ,
,  (Строгие неравенства),
(Строгие неравенства),  ,
,  (Нестрогие неравенства).
(Нестрогие неравенства).
 a<x<b
a<x<b
 >0
>0 

 NcZcQcR
NcZcQcR

















 >
> 
 -
-  =
=  ≥ 0
≥ 0 и -2; 0,2 и 5; 2 -
и -2; 0,2 и 5; 2 -  и 2 +
и 2 +  .
. | ≥ 2
| ≥ 2 ≥ 0?
≥ 0?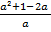 =
=  > 0
> 0