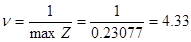ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задания для контрольной работы
Теория игр Контрольная работа по дисциплине «Теория игр» состоит из 5 заданий по 20 вариантов в каждом задании. Номер варианта (1-20) определяется двумя последними цифрами зачетной книжки студента, если эти цифры образуют число от 01 до 20. Если это число больше 20, то из него следует вычесть число, кратное 20 (20, 40, 60, 80), для попадания в отрезок 1-20.
Рекомендуемая литература Методическая литература: Набоких А.А., Ряттель А.В. Контрольная тетрадь по теории игр: Контрольные задания, программа, методические рекомендации для студентов-заочников экономического направления. – Киров: ФГБОУ ВПО Вятская ГСХА, 2012. – 40 с. Основная литература: 1. Колесник Г. В. Теория игр. – М.: Либроком, 2012. – 152 с. 2. Меньшиков И. С. Лекции по теории игр и экономическому моделированию. – М.: Контакт Плюс, 2010. – 336 с. 3. Оуэн Г. Теория игр. – М.: ЛКИ, 2010. – 198 с. 4. Петросян Л.А., Зенкевич Н. А., Шевкопляс Е. В. Теория игр. – СПб.: БХВ-Петербург, 2012. – 432 с. 5. Ященко Н. А., Лабскер Л. Г. Теория игр в экономике. Практикум с решением задач. – М.: Кнорус, 2011. – 264 с. Дополнительная литература: 1. Воробьев Н.Н. Теория игр для экономистов-кибернетиков. – М.: Наука, 1985. – 272 с. 2. Меньшиков И.С. Лекции по теории игр и экономическому моделированию. – М.: МЗ Пресс, 2006. – 208 с. 3. Ногин В.Д. Принятие решения в многокритериальной среде: количественный подход. – М.: Физматилит, 2004. – 176 с. 4. Розен В.В. Математические модели принятия решений в экономике. – М.: Высшая школа, 2002. – 288 с. 5. Саати Т. Принятие решений. Метод анализа иерархий. – М.: Радио и связь, 1993. – 278 с.
Задания для контрольной работы I. Продавец руководствуется одной из трех стратегий: назначить твердую цену a рублей за некоторый товар; установить первоначальную цену а рублей и затем сбавлять (в процессе торговли с покупателем) по b рублей вплоть до c рублей; назначить твердую цену d рублей. Покупатель выбирает одну из трех стратегий: купить товар за a, a-2b, c рублей соответственно. Требуется: а) составить платежную матрицу игры (элементами платежной матрицы является выручка продавца от продажи единицы товара); б) найти решение игры в чистых стратегиях.
II. Сельскохозяйственное предприятие имеет возможность выращивать две культуры. Прибыль предприятия от реализации выращенной культуры зависит от объема полученной. Урожай первой культуры выше при сухой погоде, а второй — при более влажной. Состояние погоды в летний период можно рассматривать как следующие стратегии природы: 1. Лето жаркое сухое. 2. Лето жаркое влажное. 3. Лето теплое сухое. 4. Лето теплое влажное. 5. Лето прохладное сухое. 6. Лето прохладное влажное. Стратегии предприятия: 1. Выращивать первую культуру. 2. Выращивать вторую культуру. Предприятие считается игроком А, природа – игроком В. Расчеты прибыли предприятия в зависимости от состояния погоды сведены в матрицу (в млн. руб.). Требуется определить оптимальные стратегии поведения сельскохозяйственного предприятия. 1 вариант 2 вариант 3 вариант 4 вариант 5 вариант 6 вариант 7 вариант 8 вариант 9 вариант 10 вариант 11 вариант 12 вариант 13 вариант 14 вариант 15 вариант 16 вариант 17 вариант 18 вариант 19 вариант 20 вариант
III. Две отрасли могут осуществлять капитальные вложения в три объекта. I-тая стратегия отрасли состоит в финансировании i-того объекта(i-1,2,3). Учитывая особенности вкладов и местные условия, прибыль первой отрасли выражается следующей матрицей. Величина прибыли первой отрасли считается равной величине убытка второй отрасли. Найти оптимальные стратегии отраслей. 1 вариант
2 вариант
3 вариант
4 вариант
5 вариант
6 вариант
7 вариант
8 вариант
9 вариант
10 вариант
11 вариант
12 вариант
13 вариант
14 вариант
15 вариант
16 вариант
17 вариант
18 вариант
19 вариант
20 вариант
IV. Предприятие должно определить уровень выпуска продукции и предоставления услуг на некоторый период времени так, чтобы удовлетворить потребности клиентов. Точная величина спроса на продукцию и услуги неизвестна, но ожидается, что в зависимости от соотношения сил на рынке товаров, действий конкурентов и погодных условий спрос может принять одно из пяти возможных значений: П1, П2, П3, П4, П5 изделий. Для каждого из возможных значений спроса существует наилучший уровень предложения А1, А2, А3, А4, А5, с точки зрения возможных затрат и прибыли, отклонение от этих уровней связано с риском и может привести к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса. Данная ситуация представлена в виде платежной матрицы игры (в у.е.). Требуется определить наилучшую стратегию поведения на рынке товаров и услуг: а) в условиях неопределенности (γ – показатель пессимизма); б) в условиях риска, считая, что ранее проведенные маркетинговые исследования позволили определить возможные вероятности возникновения этих ситуаций, которые соответственно составили Вариант 1 (γ=0,2)
Вариант 2 (γ=0,3)
Вариант 3 (γ=0,4)
Вариант 4 (γ=0,5)
Вариант 5 (γ=0,4)
Вариант 6 (γ=0,3)
Вариант 7 (γ=0,5)
Вариант 8 (γ=0,3)
Вариант 9 (γ=0,4)
Вариант 10 (γ=0,5)
Вариант 11 (γ=0,3)
Вариант 12 (γ=0,4)
Вариант 13 (γ=0,5)
Вариант 14 (γ=0,4)
Вариант 15 (γ=0,5)
Вариант 16 (γ=0,3)
Вариант 17 (γ=0,2)
Вариант 18 (γ=0,25)
Вариант 19 (γ=0,3)
Вариант 20 (γ=0,4)
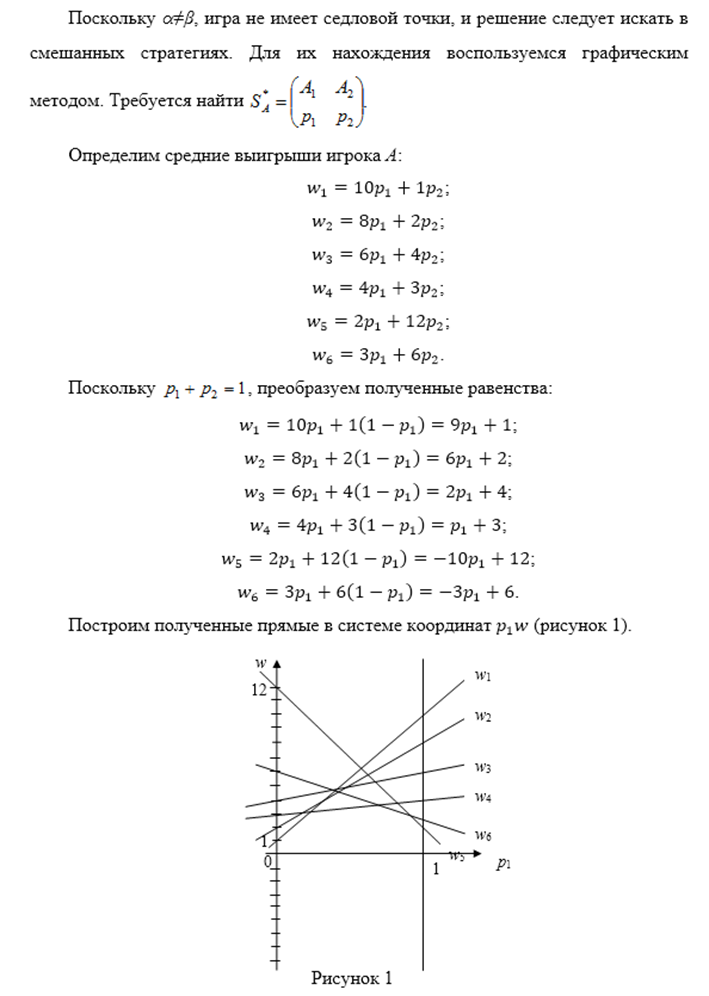
V. Небольшая фирма (игрок А) намерена сбыть крупную партию товара на одном из двух рынков, контролируемых другой, более крупной фирмой (игрок В). Для этого она может предпринять на одном из рынков соответствующие действия (например, развернуть рекламную кампанию). Господствующий на рынках игрок В может попытаться воспрепятствовать этому, предприняв на одном из двух рынков предупредительные меры. Игрок А, не встретивший на рынке препятствий, захватывает его; встретившись с сопротивлением – терпит поражение. Проникновение игрока А на первый рынок более выгодно для него, чем проникновение на второй, но борьба за первый рынок требует больших средств: победа игрока А на первом рынке принесет ему вдвое больший выигрыш, чем на втором, но зато поражение на первом рынке полностью его разоряет, а игрока В избавляет от конкурента. При поражении фирмы А на втором рынке ее потери будут не столь разорительны, но и победа принесет немного. Указанная игра задается следующими матрицами выигрышей. Найти оптимальные стратегии фирм. 1 вариант 3 вариант 5 вариант 7 вариант 9 вариант 11 вариант 13 вариант 15 вариант 17 вариант 19 вариант
III. Две отрасли могут осуществлять капитальные вложения в три объекта. I-я стратегия отрасли состоит в финансировании i-го объекта (i=1,2,3). Учитывая особенности вкладов и местные условия, прибыль первой отрасли выражается матрицей Величина прибыли первой отрасли считается равной величине убытка второй отрасли. Найти оптимальные стратегии отраслей. Решение: Определим нижнюю и верхнюю цену игры.
Так как α=-2 ≠ β=2, то игра не имеет седловой точки. В игре нет дублирующих и доминируемых стратегий. Решаем игру путем решения пары двойственных задач линейного программирования. Прибавим к каждому элементу платежной матрицы число 3, получим
Математические модели пары двойственных задач линейного программирования будут следующие
Решаем задачи линейного программирования в Excel, используя процедуру Поиск решения. Сначала вводим исходные данные.
Далее вводим коэффициенты из ограничений и вводим необходимые формулы.
Используем команду Данные – Поиск решения и заполняем необходимые параметры.
Находим решение:
Таким образом, х1=0,19231; х2=0; х3=0,03846 и минимум функции F=0,23077. Находим оптимальную смешанную стратегию игрока А, т.е. цену игры и вероятности использования стратегий:
р1=х1*v=0,19231*4,33=0,833 р2=х2*v=0*4,33=0 р3=х3*v=0,03846*4,33=0,167 Поскольку в начале решения задачи ко всем элементам было прибавлено число 3, то окончательной оптимальной ценой игры является v=1,33 (4,33-3). Получим оптимальную стратегию для игрока А - Аналогично найдем решение двойственной задачи, т.е. решение игры для игрока В.
Таким образом, у1=0,15385; у2=0; х3=0,07692 и максимум функции Z=0,23077. Находим оптимальную смешанную стратегию игрока B, т.е. цену игры и вероятности применения стратегий:
q1=y1*v=0,15385*4,33=0,667 q2=y2*v=0*4,33=0 q3=y3*v=0,07692*4,33=0,333 Ценой игры является v=1,33 (4,33-3). Оптимальная стратегия для игрока В - Первая отрасль все свои капитальные вложения может распределить по объектам в долях, соответствующих вероятностям применения своих стратегий: в первый объект 83,3%, во второй объект 0% и в третий объект 16,7% имеющихся средств. Вторая отрасль распределяет капитальные вложения по объектам в следующих долях: в первый объект 66,7%, во второй объект 0% и в третий объект 33,3% имеющихся средств.
|



 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;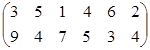 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;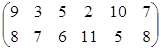 ;
; .
.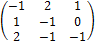


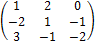







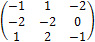








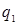 ,
,  ,
,  ,
,  ,
,  .
.
 2 вариант
2 вариант 


 4 вариант
4 вариант 


 6 вариант
6 вариант 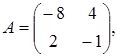


 8 вариант
8 вариант 


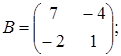 10 вариант
10 вариант 


 12 вариант
12 вариант 


 14 вариант
14 вариант 


 16 вариант
16 вариант 
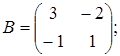

 18 вариант
18 вариант 


 20 вариант
20 вариант 





 .
. 2
2

 =-2
=-2  =2
=2 .
. при ограничениях
при ограничениях 
 при ограничениях
при ограничениях