 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Уравнения прямой и плоскости
Практическое занятие 36 Уравнения сферы, плоскости и прямой. Форма проведения: Практическая Цели урока: Обучающая: закрепить понятие уравнения сферы,плоскостии прямой Развивающая: развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию; интерес к предмету; творческие способности учащихся. Воспитывающая: воспитывать взаимопомощь у учащихся через работу в группах; уважение к мнению других. Оборудование: раздаточный материал: карточки с заданиями, заготовки для вывода уравнения сферы, шкалы для оценки урока на этапе рефлексия, маркеры, магниты, чистые листы; глобус, разминка для глаз в виде полушарий земной поверхности; мультимедийные обеспечение. Ход урока Девиз урока Математику нельзя изучать, наблюдая, как это делает сосед! Древнегреческий поэт Нивен Уравнения прямой и плоскости Уравнение прямой на плоскости в декартовой системе координат можно задать уравнением вида
для случая, когда прямая не параллельна оси OY, и уравнением
для вертикальной прямой. Но прямая может быть также задана и другим способом. Достаточно указать вектор направления этой прямой
в котором параметр t пробегает все значения числовой прямой. Координаты точки, соответствующей некоторому значению этого параметра, определяются соотношениями
Прямую в пространстве тоже можно задавать параметрическим уравнением, которое очень легко получить из предыдущего простым переходом от двумерных векторов к трехмерным. Пусть
Как известно из элементарной геометрии, через любые три точки в пространстве проходит плоскость. С другой стороны, через каждую точку плоскости можно провести единственную прямую, перпендикулярную данной плоскости. При этом все эти прямые будут параллельны друг другу, а значит, они имеют общий вектор направления. Этот вектор будем называть нормалью к плоскости. Если длина вектора равна единице, мы будем называть его единичной нормалью. В компьютерной графике часто приходится решать задачу построения нормали к некоторой плоскости, заданной тремя точками, а также задачи пересечения прямой с плоскостью и двух плоскостей. Плоскость в пространстве можно задать, указав вектор нормали к ней и какую-либо точку, принадлежащую данной плоскости. Пусть
Раскрывая это выражение в координатном виде, получаем
Теперь перепишем это уравнение в виде
где В алгоритмах компьютерной графики довольно часто приходится сталкиваться с задачей построения плоскости, проходящей через три заданные точки. Пусть три точки
Остается определить значение
следовательно
и после подстановки окончательно получим:
В большинстве алгоритмов, использующих плоскости, достаточно знать нормаль к ней и какую-либо точку, принадлежащую плоскости. Очевидно, что по аналогии можно вывести каноническое уравнение прямой на плоскости, если задана нормаль к ней и принадлежащая прямой точка. Уравнение сферы Найдем уравнение сферы радиуса R с центром в точке O1(x0;y0;z0). Согласно определению сферы расстояние любой ее точки М(х; у; z) от центра O1(x0;y0;z0) равно радиусу R, т. е. O1M= R. Но
Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере. Если центр сферы Ο1 совпадает с началом координат, то уравнение сферы принимает вид Если же дано уравнение вида F(x;y;z) = 0 , то оно, вообще говоря, определяет в пространстве некоторую поверхность. Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y; z)=0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается». Так, уравнению Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач: 1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности. 2. Дано уравнение F(x;y;z) = 0. Исследовать форму поверхности, определяемой этим уравнением.
Вариант №1. 1. Сфера задана уравнением (x – 1)2 + y 2 + (z – 2)2 = 9. 1. Найдите координаты центра и радиуса сферы. 2. Определите, принадлежат ли данной сфере точки А(1; 3; -1) и В(2; 2; 1). 2. Сфера с центром в точке О(0; 1; -2) проходит через точку А(-3; 1; 2). 1. Составьте уравнение сферы. 2. Найдите координаты точек оси абсцисс, принадлежащих данной сфере. 3. Точки А(1; 2; -3) и В(7; 2; 5) лежат на сфере радиуса 13. Найдите расстояние от центра сферы до прямой АВ. Вариант №2. 1. Сфера задана уравнением x 2 + (y +3)2 + (z – 2)2 = 25. 1. Найдите координаты центра и радиуса сферы. 2. Определите, принадлежат ли данной сфере точки А(4; -3; -1) и В(0; 1; 3). 2. Сфера с центром в точке О(-1; 0; 2) проходит через точку А(1; 2; 1). 1. Составьте уравнение сферы. 2. Найдите координаты точек оси ординат, принадлежащих данной сфере. 3. Точки А(1; 5; 6) и В(1; -1; -2) лежат на сфере, центр которой удален от середины отрезка АВ на 12. Найдите радиус сферы. Вариант №3. 1. Сфера задана уравнением x 2 + y 2 + z 2 + 2y – 4z = 4. a) Найдите координаты центра и радиуса сферы. b) Найдите значение m, при котором точки А(0; m; 2) и В(1; 1; m - 2) принадлежат данной сфере. 2. Диаметр сферы – отрезок АВ с концами А(2; -1; 4) и В(2; 7; 10). a) Составьте уравнение сферы. b) Найдите кратчайшее расстояние от точки данной сферы до плоскости Оxy. 3. Сфера задана уравнением (x + 3)2 + (y – 4)2 + (z + 1)2 = 25. Найдите длину линии, по которой данная сера пересекается с плоскостью Оyz. |





 и какую-нибудь точку
и какую-нибудь точку  , лежащую на этой прямой. При этом точки, лежащие на прямой, могут быть заданы с использованием векторных операций в виде так называемого параметрического уравнения прямой
, лежащую на этой прямой. При этом точки, лежащие на прямой, могут быть заданы с использованием векторных операций в виде так называемого параметрического уравнения прямой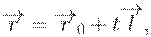

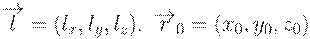 . Тогда это уравнение будет определять прямую в пространстве, а координаты точек этой прямой будут определяться формулами
. Тогда это уравнение будет определять прямую в пространстве, а координаты точек этой прямой будут определяться формулами
 - вектор единичной нормали, а
- вектор единичной нормали, а  - некоторая точка на плоскости. Тогда для любой точки
- некоторая точка на плоскости. Тогда для любой точки  , лежащей на плоскости, вектор
, лежащей на плоскости, вектор  будет ортогонален вектору нормали, а следовательно, выполняется равенство
будет ортогонален вектору нормали, а следовательно, выполняется равенство


 . Это уравнение называется каноническим уравнением плоскости. При этом совершенно ясно, что если все это уравнение умножить на какой-либо отличный от нуля множитель, то оно будет описывать ту же самую плоскость, т.е. коэффициенты
. Это уравнение называется каноническим уравнением плоскости. При этом совершенно ясно, что если все это уравнение умножить на какой-либо отличный от нуля множитель, то оно будет описывать ту же самую плоскость, т.е. коэффициенты  для каждой плоскости задаются с точностью до произвольного ненулевого множителя. Но если при этом вектор
для каждой плоскости задаются с точностью до произвольного ненулевого множителя. Но если при этом вектор 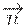 имеет единичную длину, то
имеет единичную длину, то  задает расстояние от начала координат до данной плоскости.
задает расстояние от начала координат до данной плоскости. ,
,  и
и  , не лежащие на одной прямой, имеют координатами
, не лежащие на одной прямой, имеют координатами  и
и  . Для канонического уравнения необходимо построить нормаль к плоскости, что легко можно осуществить, используя операцию векторного произведения. Поскольку векторы
. Для канонического уравнения необходимо построить нормаль к плоскости, что легко можно осуществить, используя операцию векторного произведения. Поскольку векторы  и
и  лежат в искомой плоскости, то вектор
лежат в искомой плоскости, то вектор  будет ортогонален этой плоскости. Пусть
будет ортогонален этой плоскости. Пусть  , тогда уравнение плоскости будет иметь вид
, тогда уравнение плоскости будет иметь вид
 . Так как точка
. Так как точка 
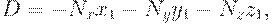

 , где
, где  . Следовательно,
. Следовательно,
 .
. не удовлетворяют никакие действительные значения х, у, z. Уравнению
не удовлетворяют никакие действительные значения х, у, z. Уравнению  удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, а х — любое число).
удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, а х — любое число).