 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Общая формула для погрешности 12
(Прямая задача теории погрешностей) Прямая (основная) задача теории погрешностей заключается в вычислении погрешности результата математических действий, если известны погрешности аргументов. При этом действия над аргументами можно представить в виде функции
Предельная абсолютная погрешность функции
Предельная относительная погрешность функции
Формула (1.13) получена путем деления (1.12) на модуль Пример 1.1
Из этого следует, что предельная абсолютная погрешность суммы, не может быть меньше предельной абсолютной погрешности наименее точного (в смысле абсолютной погрешности) из слагаемых, т.е. слагаемого, имеющего максимальную абсолютную погрешность. Следовательно, с какой бы степенью точности не были определены остальные слагаемые, мы не можем за их счет увеличить точность суммы. Поэтому не имеет смысла сохранять излишние знаки и в более точных слагаемых. Отсюда вытекает следующее, обычно применяемое, практическое правило для сложения приближенных чисел: - выделить числа, десятичная запись которых обрывается ранее других и оставить без изменения; - остальные числа округлить по образцу выделенных, сохраняя один или два запасных десятичных знака; - произвести сложение данных чисел, учитывая все сохраненные знаки; - полученный результат округлить на один знак. Пример 1.2
Из результата вычисления Исходя из вышесказанного, получаем еще одно практическое правило: - при приближенных вычислениях следует избегать вычитания двух почти равных приближенных чисел; - если же приходится вычитать такие числа, то следует преобразовывать такие выражения, или (если такая возможность имеется) уменьшаемое и вычитаемое брать с достаточным числом запасных верных знаков. Т.о., примеры на определение погрешности суммы, разности, произведения, частного, корня, степени дали возможность выработать рекомендации по выполнению массовых вычислений( без точного учета погрешностей ): - при сложении и вычитании младший сохраненный десятичный разряд результата должен являться наибольшим среди десятичных разрядов, выражаемых последними значащими цифрами исходных данных; - при умножении, делении следует сохранять столько значащих цифр, сколько их имеет исходное данное с наименьшим числом верных цифр; - при возведении в степень следует сохранять столько значащих цифр, сколько верных цифр основания степени. - при извлечении корня в результате следует брать столько значащих цифр, сколько верных цифр имеет подкоренное выражение; - если некоторые данные имеют излишние младшие десятичные разряды (при сложении и вычитании) или больше значащих цифр, чем другие (при умножении, делении, возведении в степень, извлечении корня), то их предварительно нужно округлить, сохраняя одну (две) запасные цифры; - во всех промежуточных результатах следует сохранять на одну (две) цифры больше, чем рекомендуют предыдущие правила, в окончательном результате одна из оставленных цифр отбрасывается.
Обратная задача теории Погрешностей 12 |



 ,
,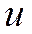 - дифференцируемая функция;
- дифференцируемая функция; - предельные абсолютные погрешности аргументов
- предельные абсолютные погрешности аргументов  .
. , (1.12)
, (1.12) (1.13)
(1.13) .
.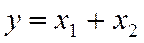 ,
, 


 ,
, 


 вытекает, что
вытекает, что  может быть весьма большой, если приближенные числа
может быть весьма большой, если приближенные числа  и
и  достаточно близки друг к другу, в то время как их погрешности (абсолютные и относительные) остаются малыми, т.е. т.о. происходит потеря точности.
достаточно близки друг к другу, в то время как их погрешности (абсолютные и относительные) остаются малыми, т.е. т.о. происходит потеря точности.