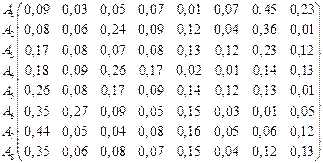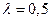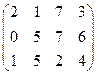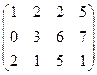ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Рівномірно розподілені випадкові числа
Лабораторна робота № 4. Розв’язати матричну гру, знайшовши стратегії гравців аналітично і графічно | 1. | 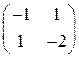 | 2. |  | 3. |  | 4. |  | | 5. |  | 6. |  | 7. |  | 8. |  | | 9. | 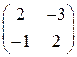 | 10. |  | 11. |  | 12. |  | | 13. |  | 14. |  | 15. | 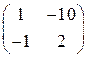 | 16. | 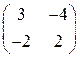 | | 17. |  | 18. |  | 19. |  | 20. |  | | 21. |  | 22. | 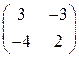 | 23. |  | 24. | 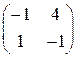 | | 25. |  | 26. |  | 27. |  | 28. |  | | 29. |  | 30. |  | | | | |
Лабораторна робота № 5. Варіант № 1Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 2Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 3Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.  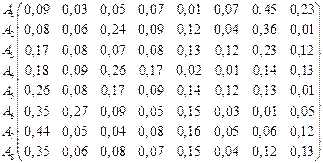 | Варіант № 4Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 5Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 6Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 7.Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 8.Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 9Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 10Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 11Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 12Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 13 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 14 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца. 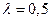  | Варіант № 15 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 16 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 17 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 18 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 19 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 20 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 21Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 22 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца. 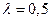  | Варіант № 23 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 24 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 25Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 26 Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 27Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 28Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 29Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца.   | Варіант № 30Знайти оптимальні стратегії  , використовуючи критерії Вальда, Севіджа і Гурвіца. , використовуючи критерії Вальда, Севіджа і Гурвіца. 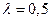  |
Лабораторна робота № 6 Варіант № 1 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 2 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 3 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 4 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 5 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування 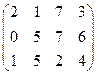 | Варіант № 6 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 7 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 8 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 9 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 10 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 11 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 12 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 13 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 14 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 15 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  |
Варіант № 16 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 17 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 18 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування 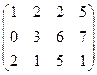 | Варіант № 19 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 20 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 21 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 22 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 23 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 24 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 25 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 26 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 27 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 28 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 29 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  | Варіант № 30 Знайти розв’язок матричної гри, звівши її до задачі лінійного програмування  |
|




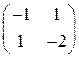







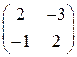





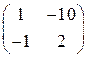
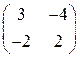




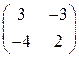

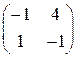






 , використовуючи критерії Вальда, Севіджа і Гурвіца.
, використовуючи критерії Вальда, Севіджа і Гурвіца.