ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Функция ПС предназначена для расчета текущей стоимости и является обратным к определению будущей стоимости БС.
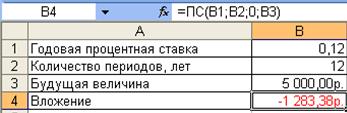
Синтаксис ПС(ставка ;кпер;плт;бс;тип) Бс — требуемое значение будущей стоимости (или остатка средств после последней выплаты). Виды расчетов 1) Если известно будущее значение вклада (займа), то требуется определить сумму, которую необходимо положить на счет сегодня, чтобы в конце n-го периода она достигла заданного значения Пример. Сколько фирме требуется положить денег сегодня на депозит единым вкладом, чтобы через 12 лет он достиг 5000 ден.ед. при ставке 12%. Заполнение листа Excel.
2) Требуется найти текущую стоимость будущих периодических постоянных платежей, которые производятся в начале или в конце каждого расчетного периода. Продолжаем заполнять тот же лист Excel, который назовем ПС. Пример. Сколько денег должно быть в бюджете компании в начале года, чтобы она могла ежемесячно выплачивать 600 ден. Ед. за оборудование при ежемесячной ставке в 0,4%.
Что выгодней? Пример . Получено наследство 50000 ден.ед. В течение года эти деньги не понадобятся. На какой вклад их выгоднее положить: – с ежемесячным начислением 2,5% – с ежеквартальным начислением 8% – депозит на 6 месяцев под 32% годовых – депозит на 12 месяцев под 36% годовых. Решение. Используем функцию БС, заполняем лист Excel.
Вывод. Выгоднее положить деньги на вклад с ежеквартальным начислением 8%. Пример . Рассматриваются два варианта покупки дома: заплатить сразу 99000 ден. ед. или в рассрочку по 940 ден.ед. ежемесячно в течение 15 лет. Какой вариант предпочтительнее, если ставка 8% годовых? Решение. В задаче необходимо сравнить, что выгоднее: заплатить сегодня указанную сумму или растянуть платежи на определенный срок. Для сравнения следует привести эти денежные потоки к одному периоду времени, т.е. рассчитать текущую стоимость будущих фиксированных периодических выплат. Используем функцию ПС, заполняем лист Excel.
Вывод. Запрашиваемая цена 99000 ден.ед. больше рассчитанной текущей стоимости периодических выплат, следовательно, не выгодно покупать дом сразу, лучше растянуть платежи на 15 лет. Пример . Родственник завещал 240 тыс. руб., вложенных в ценные бумаги, дающие доход по 20 тыс. руб. в год. И которые можно получить либо в течение 12 лет по этой сумме либо целиком, но через 15 лет, когда подойдет срок погашения ценных бумаг и сумма капитала составит 300 тыс.руб. Решение. Чтобы решить, какой вариант является более выгодным, надо рассчитать текущую стоимость капитала в каждом случае. Используем функцию ПС, заполняем лист тот же Excel.
Вывод. Будущее значение в размере 300 тыс.руб. через 15 лет, пересчитанное на настоящее время, составит всего 71,8 тыс. руб. Разница двух вариантов получения денег составляет 136,27–71,8 = 64,45 тыс. руб., что говорит о предпочтительности второго варианта. Кредитные расчеты Кредит – это деньги, переданные в распоряжение кому–нибудь на определенный период времени, в течение которого он должен выплачивать владельцу денег определенные проценты за их использование, а в конце указанного периода возвратить всю одолженную сумму. Как правило, кредит (заем) погашается одинаковыми платежами в конце каждого расчетного периода. Будущая стоимость платежей будет равна сумме займа с начисленными процентам к концу последнего расчетного периода. Текущая стоимость выплат по займу должна равняться настоящей сумме займа. В схему погашения займа входит расчет постоянных периодических платежей, необходимых для равномерного погашения займа (функция ПЛТ). Эти платежи включают в себя сумму процентов по непогашенной части займа и основную выплату по займу, которые зависят от номера периода, не включают в себя налоги и другие сборы.
Функция ПЛТ Функция вычисляет величину выплаты за один период на основе фиксированных периодических выплат и постоянной процентной ставки. Выплаты, рассчитанные этой функцией, включают основные платежи и платежи по процентам. СинтаксисПЛТ(ставка;кпер;пс;бс;тип) Ставка — процентная ставка за период займа Кпер — общее число периодов выплат. Пс — приведенная (нынешняя) стоимость – общая сумма, на настоящий момент равноценная серии будущих выплат. Бс —будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Пример. Необходимо накопить 10000 руб. за два года, откладывая в конце месяца постоянную сумму. Какова должна быть эта сумма, если деньги размещаются при условии 9 % годовых.
Постановка задачи. Взят кредит на определенный срок; погашение кредита будет происходить равномерными платежами в конце каждого периода. Чтобы проанализировать свои возможности, нужно составить план погашения кредита по этапам, определив размер периодического платежа с распределением, какая часть платежа идет на погашение основного долга, а какая – на выплату процентов. Пример. Составить схему погашения займа в 70000 ден. = ед., выданного сроком на 3 года под 17% годовых.
Функция ПРПЛТ вычисляет платежи по процентам за заданный период на основе периодических постоянных выплат и постоянной процентной ставки. СинтаксисПРПЛТ(ставка;период;кпер;пс;бс;тип) Период–конкретный период, для которого нужно определить сумму выплаты. Функция ОСПЛТ вычисляет величину основного платежа по займу.. СинтаксисОСПЛТ(ставка;период;кпер;пс;бс;тип) В результате получим таблицу
На что следует обратить внимание: а) сумма займа на конец года (остаток) в последнем периоде равна нулю; б) сумма основного платежа по займу за все периоды равна величине займа. По таблице строим диаграмму с областями, выделив диапазон D2:E5; заголовок: Рисунок 1 – Распределение платежей; подпись по оси Х – годы.
Выбор кредита Коммерсант собирается взять кредит размером 100000 ден.ед. сроком на несколько лет. Он обратился в три банка. Банки «Север», «Запад» и «Юг» предоставляют кредит под 24%, 25% и 25% годовых со сроками погашения 7, 6 и 5 лет. Издержки при оформлении кредита соответственно 300, 300 и 250 руб. Необходимо сравнить условия кредитования, и для выбранных условий составить план погашения кредита. Для выбора банка составляется следующая таблица.
Полученная сумма определяется как разница между суммой кредита и издержками оформления. Далее вычисляются ежегодные платежи и отношение платежа к полученной сумме.
Если срок погашения для коммерсанта не важен, то ему лучше выбрать банк «Север». Далее на этом листе составляем таблицу погашения займа.
|