 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Модуль «РЕАЛЬНАЯ МАТЕМАТИКА»
Вариант 1 Часть 1 Модуль «АЛГЕБРА» 1. Найдите значение выражения  2. Одна из точек, отмеченных на координатной прямой, соответствует числу  Какая это точка? Какая это точка? 
В ответе укажите номер правильного варианта. 1) точка A, 2) точка B, 3) точка C, 4) точка D 3. Значение какого из выражений является числом иррациональным? В ответе укажите номер правильного варианта. 1)  2) 2)  3)  4) 4)  4. Найдите корни уравнения  . . Если корней несколько, запишите их через точку с запятой в порядке возрастания. 5. Найдите значение выражения 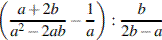 при при  6. Установите соответствие между графиками функций и формулами, которые их задают. 
1)  2) 2)  3) 3)  4) 4)  Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке. 7. Упростите выражение  и найдите его значение при и найдите его значение при  . . 8. Решите систему уравнений  Модуль «ГЕОМЕТРИЯ» 9. Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6. 10. Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AD. Найдите площадь трапеции AECB. 11. Сторона равностороннего треугольника равна 10  . Найдите его биссектрису. . Найдите его биссектрису. 12. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой. | 13. Какое из следующих утверждений верно? | | | 1) | Диагонали трапеции пересекаются и делятся точкой пересечения пополам | | | 2) | Все углы ромба равны. | | | 3) | Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то это квадрат. | В ответ запишите номер выбранного утверждения. | Модуль «РЕАЛЬНАЯ МАТЕМАТИКА» - Василий измерял в течение недели время, которое он тратил на дорогу до школы, а результаты записывал в таблицу.
| День недели | Пн | Вт | Ср | Чт | Пт | Сб | | Время (мин.) | | | | | | | Сколько минут в среднем занимает у Василия дорога до школы? - Суточная норма потребления витамина С для взрослого человека составляет 60 мг. В 100 г свеклы в среднем содержится 23 мг витамина С. Сколько процентов суточной нормы витамина С получил человек, съевший 100 г свеклы? Ответ округлите до целого числа.
- Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время в секундах, а по вертикальной — расстояние пловца от старта в метрах. Кто выиграл соревнование? В ответе запишите, на сколько секунд он обогнал соперника.

- Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?

- От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.

- Картинка имеет форму прямоугольника со сторонами 11 см и 13 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 675 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.

20. Закон Джоуля–Ленца можно записать в виде Q=I2 Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите сопротивление цепи R (в омах), если Q=432 Дж, I=3 A, t=6 с. Часть 2 Модуль «АЛГЕБРА» - Сократите дробь
 . . - Упростите выражение
 - Постройте график функции
 и определите, при каких значениях параметра и определите, при каких значениях параметра  прямая прямая  имеет с графиком ровно одну общую точку. имеет с графиком ровно одну общую точку. Модуль «ГЕОМЕТРИЯ» - Периметр прямоугольника равен 30, а диагональ равна 14. Найдите площадь этого прямоугольника.
- В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
- Боковые стороны AB и CD трапеции ABCD равны соответственно 24 и 40, а основание BC равно 4. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
|





 Какая это точка?
Какая это точка?
 2)
2) 
 4)
4) 
 .
.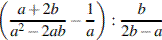 при
при 

 2)
2)  3)
3)  4)
4) 
 и найдите его значение при
и найдите его значение при  .
.
 . Найдите его биссектрису.
. Найдите его биссектрису.



 .
.
 и определите, при каких значениях параметра
и определите, при каких значениях параметра  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.