 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| УПРАВЛЯЕМАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА
по дисциплине «Теория вероятностей и математическая статистика» в 4 семестре 2015/2016 учебного года в группах ИСТ-21 и ИСТ-22.
Управляемая самостоятельная работа 1. Комбинаторные методы для нахождения вероятностей событий.
Теоретические материалы по теме см. в: Рябушко, А.П. Индивидуальные задания по высшей математике : Операционное исчисление. Элементы теории устойчивости. Теория вероятностей. Математическая статистика : учеб. пособие / А.П. Рябушко. – Минск: Вышэйшая школа, 2006. – 336 с. Стр. 125, 127–128.
Комбинаторика – это раздел математики, посвящённый решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Конечное множество из Определение 1. Упорядоченной
элементов
называются равными, если
Если каждый элемент в упорядоченной Обозначение Теорема 1. Теорема 2. Определение 2. Размещение без повторений из Обозначение
Теорема 3. Перестановки с повторениями:
Определение 3. Неупорядоченной
элементов
называются равными, если каждая из них состоит из одних и тех же элементов Обозначение Теорема 4. Теорема 5.
Схема рассуждений при решении задач по теме «Комбинаторные методы для нахождения вероятностей событий».
1) Из урны, содержащей
Р е ш е н и е. Упорядоченная Размещение без повторений из Перестановка без повторений из Число всех равновозможных элементарных событий
Событие Искомая вероятность
2) Из урны, содержащей
Р е ш е н и е. Упорядоченная Размещение с повторениями из Число всех равновозможных элементарных событий
Событие Искомая вероятность
3) Из четырёх букв разрезной азбуки составлено слово «МАТЬ». Ребёнок, не умеющий читать, рассыпал эти буквы и затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получилось слово «МАТЬ».
Р е ш е н и е. Упорядоченная 4–выборка из 4–множества без повторений. Размещение без повторений из 4 элементов по 4. Перестановка без повторений из 4 элементов. Число всех равновозможных элементарных событий Событие Искомая вероятность
3’) Из пяти букв разрезной азбуки составлено слово «ИГОРЬ». Ребёнок, не умеющий читать, рассыпал эти буквы и затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получилось слово «ИГОРЬ».
Р е ш е н и е. Упорядоченная 5–выборка из 5–множества без повторений. Размещение без повторений из 5 элементов по 5. Перестановка без повторений из 5 элементов. Число всех равновозможных элементарных событий
Событие Искомая вероятность
4) Из четырёх букв разрезной азбуки составлено слово «МАМА». Ребёнок, не умеющий читать, рассыпал эти буквы и затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получилось слово «МАМА».
Р е ш е н и е. Упорядоченная 4–выборка из 4–множества с повторениями. Размещение с повторениями из 4 элементов по 4, в котором для каждого элемента указывается число его повторений: «М» - 2; «А» - 2. Перестановка с повторениями. Число всех равновозможных элементарных событий Событие Искомая вероятность
4’) Из пяти букв разрезной азбуки составлено слово «НАИНА». Ребёнок, не умеющий читать, рассыпал эти буквы и затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получилось слово «НАИНА».
Р е ш е н и е. Упорядоченная 5–выборка из 5–множества с повторениями. Размещение с повторениями из 5 элементов по 5, в котором для каждого элемента указывается число его повторений: «Н» - 2; «А» - 2; «И» - 1. Перестановка с повторениями. Число всех равновозможных элементарных событий
Событие Искомая вероятность
4’’) Из шести букв разрезной азбуки составлено слово «БАОБАБ». Ребёнок, не умеющий читать, рассыпал эти буквы и затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получилось слово «БАОБАБ».
Р е ш е н и е. Упорядоченная 6–выборка из 6–множества с повторениями. Размещение с повторениями из 6 элементов по 6, в котором для каждого элемента указывается число его повторений: «Б» - 3; «А» - 2; «О» - 1. Перестановка с повторениями. Число всех равновозможных элементарных событий
Событие Искомая вероятность
5.1) В танцевальном баре восемь студенток и десять студентов. Объявлено: «Дамы приглашают кавалеров». Студентки выбирают себе партнёров последовательно, случайным образом, при условии, что никакие две студентки танцевать с одним студентом не могут. Найти вероятность того, что будут приглашены первые восемь студентов согласно алфавитному списку.
Р е ш е н и е. Упорядоченная 8–выборка из 10–множества без повторений. Размещение без повторений из 10 элементов по 8. Число всех равновозможных элементарных событий
Событие Упорядоченная 8–выборка из 8–множества без повторений. Размещение без повторений из 8 элементов по 8. Перестановка без повторений из 8 элементов. Число благоприятных элементарных событий
Искомая вероятность
5.2) В танцевальном баре девять студенток и одиннадцать студентов. Объявлено: «Дамы приглашают кавалеров». Студентки выбирают себе партнёров последовательно, случайным образом, при условии, что никакие две студентки танцевать с одним студентом не могут. Найти вероятность того, что будут приглашены первые девять студентов согласно алфавитному списку.
Р е ш е н и е. Упорядоченная 9–выборка из 11–множества без повторений. Размещение без повторений из 11 элементов по 9. Число всех равновозможных элементарных событий
Событие Упорядоченная 9–выборка из 9–множества без повторений. Размещение без повторений из 9 элементов по 9. Перестановка без повторений из 9 элементов. Число благоприятных элементарных событий
Искомая вероятность
5.3) В танцевальном баре десять студенток и двенадцать студентов. Объявлено: «Дамы приглашают кавалеров». Студентки выбирают себе партнёров последовательно, случайным образом, при условии, что никакие две студентки танцевать с одним студентом не могут. Найти вероятность того, что будут приглашены первые десять студентов согласно алфавитному списку.
Р е ш е н и е. Упорядоченная 10–выборка из 12–множества без повторений. Размещение без повторений из 12 элементов по 10. Число всех равновозможных элементарных событий
Событие Упорядоченная 10–выборка из 10–множества без повторений. Размещение без повторений из 10 элементов по 10. Перестановка без повторений из 10 элементов. Число благоприятных элементарных событий
Искомая вероятность
6) Батарея, состоящая из
Р е ш е н и е. Упорядоченная Размещение с повторениями из Число всех равновозможных элементарных событий
Событие Упорядоченная Размещение без повторений из Число благоприятных элементарных событий
Искомая вероятность
7.1) Пять человек случайным образом рассаживаются за круглым столом. Найти вероятность того, что два фиксированных лица А и В окажутся рядом.
Р е ш е н и е. Упорядоченная 5–выборка из 5–множества без повторений. Размещение без повторений из 5 элементов по 5. Перестановка без повторений из 5 элементов. Число всех равновозможных элементарных событий
Событие Число благоприятных элементарных событий Искомая вероятность
7.2) Шесть человек случайным образом рассаживаются за круглым столом. Найти вероятность того, что два фиксированных лица А и В окажутся рядом.
Р е ш е н и е. Упорядоченная 6–выборка из 6–множества без повторений. Размещение без повторений из 6 элементов по 6. Перестановка без повторений из 6 элементов. Число всех равновозможных элементарных событий
Событие Число благоприятных элементарных событий Искомая вероятность
8.1) Четыре человека рассаживаются случайно вдоль одной из сторон прямоугольного стола. Найти вероятность того, что два фиксированных лица А и В окажутся рядом.
Р е ш е н и е. Упорядоченная 4–выборка из 4–множества без повторений. Размещение без повторений из 4 элементов по 4. Перестановка без повторений из 4 элементов. Число всех равновозможных элементарных событий Событие Число благоприятных элементарных событий Искомая вероятность
8.2) Пять человек рассаживаются случайно вдоль одной из сторон прямоугольного стола. Найти вероятность того, что два фиксированных лица А и В окажутся рядом.
Р е ш е н и е. Упорядоченная 5–выборка из 5–множества без повторений. Размещение без повторений из 5 элементов по 5. Перестановка без повторений из 5 элементов. Число всех равновозможных элементарных событий
Событие Число благоприятных элементарных событий Искомая вероятность
9) В урне 3 белых и 5 чёрных шаров. Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми.
Р е ш е н и е. Неупорядоченная 2–выборка из 8–множества без повторений. Сочетание без повторений из 8 элементов по 2. Число всех равновозможных элементарных событий Событие Неупорядоченная 2–выборка из 3–множества без повторений. Сочетание без повторений из 3 элементов по 2. Число благоприятных элементарных событий Искомая вероятность
10) В урне 3 белых и 5 чёрных шаров. Из урны вынимают сразу пять шаров. Найти вероятность того, что два из них будут белыми, а три ‑ чёрными.
Р е ш е н и е. Неупорядоченная 5–выборка из 8–множества без повторений. Сочетание без повторений из 8 элементов по 5. Число всех равновозможных элементарных событий Событие Число благоприятных элементарных событий Искомая вероятность
11) В партии, состоящей из
Р е ш е н и е. Неупорядоченная Сочетание без повторений из Число всех равновозможных элементарных событий Событие Число благоприятных элементарных событий Искомая вероятность
12) В урне 3 белых и 5 чёрных шаров. Из урны вынимают сразу два шара. Какое событие более вероятно:
Р е ш е н и е. Неупорядоченная 2–выборка из 8–множества без повторений. Сочетание без повторений из 8 элементов по 2. Число всех равновозможных элементарных событий Число благоприятных событию Число благоприятных событию О т в е т.
13) В розыгрыше первенства по баскетболу участвуют восемнадцать команд, из которых случайным образом формируются две группы по девять команд в каждой. Среди участников соревнований имеется пять команд экстракласса. Найти вероятности следующих событий:
Р е ш е н и е. Неупорядоченная 9–выборка из 18–множества без повторений. Сочетание без повторений из 18 элементов по 9. Число всех равновозможных элементарных событий Число благоприятных событию Число благоприятных событию
14) Из полной колоды карт (52 листа, 4 масти) вынимается сразу несколько карт. Сколько карт нужно вынуть, чтобы с вероятностью, большей чем 0,50, утверждать, что среди них будут карты одной и той же масти?
Р е ш е н и е. Обозначим При При О т в е т. Нужно вынуть
Контроль УСР 1 «Комбинаторные методы для нахождения вероятностей событий»(задания из экзаменационных билетов).
Вариант 1. ИСТ-21: Колдушко С. Д, Кондратович Ю. И., Коновальчик В. Е. ИСТ-22: Аллаберенов А. А., Володько В. Л. Четыре лица случайным образом выбираются из группы, состоящей из 4 русских, 3 украинцев и 2 белорусов. Применяя комбинаторику найти вероятность того, что в выбранной четвёрке точно 1 человек будет русским.
Вариант 2. ИСТ-21: Макаренко И. А., Малентович К. А., Минько И. Н. ИСТ-22: Говор А. А., Дорошенко А. В. Четыре лица случайным образом выбираются из группы, состоящей из 4 русских, 3 украинцев и 2 белорусов. Применяя комбинаторику найти вероятность того, что в выбранной четвёрке точно 3 человека будут русскими.
Вариант 3. ИСТ-21: Пятигор А. Л., Рак А. А., Тихонов С. А. ИСТ-22: Жуков Р. С., Илистинов В. И. Четыре лица случайным образом выбираются из группы, состоящей из 4 русских, 3 украинцев и 2 белорусов. Применяя комбинаторику найти вероятность того, что в выбранной четвёрке будут 3 украинца.
Вариант 4. ИСТ-21: Усенко И. В., Хмелевский В. В., Шумский Я. Д., Яхонт В. И. ИСТ-22: Мезяк А. И., Попченя Р. С. Четыре лица случайным образом выбираются из группы, состоящей из 4 русских, 3 украинцев и 2 белорусов. Применяя комбинаторику найти вероятность того, что в выбранной четвёрке точно 1 человек будет белорусом.
Управляемая самостоятельная работа 2. Безусловные и условные вероятности событий. Зависимые и независимые события.
Теоретические материалы по теме см. в: Рябушко, А.П. Индивидуальные задания по высшей математике : Операционное исчисление. Элементы теории устойчивости. Теория вероятностей. Математическая статистика : учеб. пособие / А.П. Рябушко. – Минск: Вышэйшая школа, 2006. – 336 с. Стр. 127, 134.
Пусть пространство элементарных событий, соответствующих данному испытанию, состоит из
Обозначение
Вероятность события Аналогично определяется условная вероятность события
Пример.Брошены две игральные кости. Чему равна вероятность того, что сумма выпавших очков равна 8, если известно, что эта сумма есть чётное число.
Р е ш е н и е. Пространство элементарных событий
Событие Событие
Безусловная же вероятность события
Событие Событие
Пример. (Предыдущий.)
Р е ш е н и е.
Условие независимости события
а условие зависимости — в виде
Зависимость или независимость событий всегда взаимны. В связи с этим можно дать следующее новое определение независимых событий. Два события называются независимыми, если появление одного из них не изменяет вероятности появление другого.
Контроль УСР 2 «Безусловные и условные вероятности событий. Зависимые и независимые события» (задания из экзаменационных билетов).
Вариант 1. ИСТ-21: Колдушко С. Д, Кондратович Ю. И., Коновальчик В. Е. ИСТ-22: Аллаберенов А. А., Володько В. Л. Последовательно бросаются две монеты. Найти безусловные и условные вероятности следующих событий: А – выпадение герба на первой монете; F – выпадение герба на второй монете. Зависимы или независимы эти события?
Вариант 2. ИСТ-21: Макаренко И. А., Малентович К. А., Минько И. Н. ИСТ-22: Говор А. А., Дорошенко А. В. Из полной колоды карт (4´13=52 листа) вынимается одна карта. Найти безусловные и условные вероятности следующих событий: В – появление карты красной масти; С – появление бубнового туза. Зависимы или независимы эти события?
Вариант 3. ИСТ-21: Пятигор А. Л., Рак А. А., Тихонов С. А. ИСТ-22: Жуков Р. С., Илистинов В. И. Последовательно бросаются две монеты. Найти безусловные и условные вероятности следующих событий: D – выпадение хотя бы одного герба; F – выпадение герба на второй монете. Зависимы или независимы эти события?
Вариант 4. ИСТ-21: Усенко И. В., Хмелевский В. В., Шумский Я. Д., Яхонт В. И. ИСТ-22: Мезяк А. И., Попченя Р. С. Из неполной колоды карт (4´9=36 листов) вынимается одна карта. Найти безусловные и условные вероятности следующих событий: А – появление туза; С – появление бубнового туза. Зависимы или независимы эти события?
Управляемая самостоятельная работа 3. Неравенство П. Л. Чебышёва.
Теоретические материалы по теме см. в: Рябушко, А.П. Индивидуальные задания по высшей математике : Операционное исчисление. Элементы теории устойчивости. Теория вероятностей. Математическая статистика : учеб. пособие / А.П. Рябушко. – Минск: Вышэйшая школа, 2006. – 336 с. Стр. 219-220.
Пусть
Отсюда при
3.1. Неравенство П. Л. Чебышёва. Каково бы ни было
1) Электростанция обслуживает сеть из 18000 ламп, вероятность включения каждой из которых в зимний вечер равна 0,9. Какова вероятность того, что число ламп, включённых в сеть зимним вечером, отличается от своего математического ожидания по абсолютной величине не более чем на 200?
Р е ш е н и е. Согласно условию дискретная случайная величина
О т в е т.
2) Дискретная случайная величина
Чему равна вероятность того, что
Р е ш е н и е. Шаг 1. По определению математическое ожидание
Шаг 2. По теореме дисперсия
Шаг 3. Неравенству
удовлетворяют следующие значения случайной величины
Искомая вероятность также может быть найдена путём перехода к противоположному событию
Шаг 4. Согласно неравенству Чебышёва
О т в е т. Вероятность
2’) Дискретная случайная величина
Чему равна вероятность того, что
Р е ш е н и е. Шаг 1. По определению математическое ожидание
Шаг 2. По теореме дисперсия
Шаг 3. Неравенству
удовлетворяют следующие значения случайной величины
Искомая вероятность также может быть найдена путём перехода к противоположному событию
Шаг 4. Согласно неравенству Чебышёва
О т в е т. Вероятность
3) Средняя длина детали 50 см, а дисперсия 0,1. Пользуясь неравенством Чебышёва, оценить вероятность того, что случайно взятая деталь окажется по длине не меньше 49,5 см и не больше 50,5 см.
Р е ш е н и е. Пусть
то необходимо оценить снизу вероятность
О т в е т.
3.2. Теорема П. Л Чебышёва. Пусть
4) Для определения средней продолжительности горения электроламп в партии из 200 одинаковых ящиков было взято на выборку по одной лампе из каждого ящика. Оценить снизу вероятность того, что средняя продолжительность горения отобранных 200 электроламп отличается от средней продолжительности горения во всей партии по абсолютной величине меньше чем на 5 ч, если известно, что среднее квадратичное отклонение продолжительности горения ламп в каждом ящике меньше 7 ч.
Р е ш е н и е. Пусть дискретная случайная величина
а средняя продолжительность горения ламп во всей партии
В задаче требуется оценить снизу вероятность
Так как Итак, искомая вероятность
О т в е т.
5) Сколько раз нужно измерить данную величину, истинное значение которой равно
Р е ш е н и е. Пусть дискретная случайная величина
Требуется найти такое
Согласно обобщённому неравенству Чебышёва
где следует положить
О т в е т.
6) Выяснить, применимо ли обобщённое неравенство Чебышёва к последовательности независимых случайных величин |



 элементов называется кратко
элементов называется кратко  –множеством.
–множеством. ‑множества
‑множества  называется любое упорядоченное
называется любое упорядоченное 
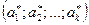

 .
. , то она называется размещением без повторений из
, то она называется размещением без повторений из  (здесь обязательно
(здесь обязательно  ). Если хотя бы один элемент в упорядоченной
). Если хотя бы один элемент в упорядоченной  , то она называется размещением с повторениями из
, то она называется размещением с повторениями из  (здесь может быть
(здесь может быть  ). ■
). ■ .
. .
. . ■
. ■ .
. .
.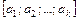

 (здесь обязательно
(здесь обязательно  (здесь может быть
(здесь может быть  .
. .
.
 .
. . Число благоприятных элементарных событий
. Число благоприятных элементарных событий  .
. . ■
. ■ .
. . Число благоприятных элементарных событий
. Число благоприятных элементарных событий  . ■
. ■ .
. . Число благоприятных элементарных событий
. Число благоприятных элементарных событий  . ■
. ■ .
.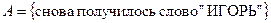 . Число благоприятных элементарных событий
. Число благоприятных элементарных событий  . ■
. ■ .
. . Число благоприятных элементарных событий
. Число благоприятных элементарных событий 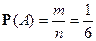 . ■
. ■ .
.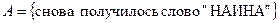 . Число благоприятных элементарных событий
. Число благоприятных элементарных событий  . ■
. ■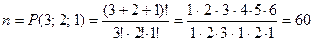 .
. . Число благоприятных элементарных событий
. Число благоприятных элементарных событий  . ■
. ■ .
. .
. .
. . ■
. ■ .
. .
. .
. . ■
. ■ .
. .
. .
. . ■
. ■ самолётов (
самолётов ( 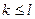 ). Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, что все
). Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, что все  .
. .
. .
.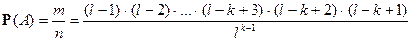 .■
.■ .
. .
. .
. . ■
. ■ .
. .
. . ■
. ■ .
. .
. . ■
. ■ .
. . ■
. ■ .
. .
. .
. . ■
. ■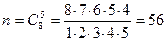 .
. .
. .
. . ■
. ■ изделий. Найти вероятность того, что из них ровно
изделий. Найти вероятность того, что из них ровно  изделий будут дефектными.
изделий будут дефектными. .
. .
. .
. . ■
. ■ ‑ шары одного цвета;
‑ шары одного цвета; ‑ шары разных цветов?
‑ шары разных цветов? . Искомая вероятность
. Искомая вероятность  .
. . Искомая вероятность
. Искомая вероятность  . ■
. ■ .
. .
. . Искомая вероятность
. Искомая вероятность  .
. . Искомая вероятность
. Искомая вероятность  . ■
. ■ наличие среди
наличие среди  число всех равновозможных элементарных событий
число всех равновозможных элементарных событий  . Число благоприятных событию
. Число благоприятных событию  элементарных случаев
элементарных случаев  . Искомая вероятность
. Искомая вероятность  .
. число всех равновозможных элементарных событий
число всех равновозможных элементарных событий  . Число благоприятных событию
. Число благоприятных событию  элементарных случаев
элементарных случаев  . Искомая вероятность
. Искомая вероятность  . ■
. ■ карт.
карт. равновозможных элементарных событий. В этом случае (безусловной) вероятностью события
равновозможных элементарных событий. В этом случае (безусловной) вероятностью события  элементарных событий, благоприятных для
элементарных событий, благоприятных для  .
. (рублёный шрифт) от слов probabitité (фр.) и probability (англ.), которые переводятся как вероятность.
(рублёный шрифт) от слов probabitité (фр.) и probability (англ.), которые переводятся как вероятность. или
или  .
. или
или  .
. . ■
. ■ .
.
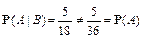
 Событие
Событие  ,
, .
. ‑ случайная величина с математическим ожиданием
‑ случайная величина с математическим ожиданием  и средним квадратичным отклонением
и средним квадратичным отклонением  . Тогда для любого
. Тогда для любого  вероятность того, что
вероятность того, что  ) чем на
) чем на  , меньше (
, меньше (  )
) 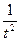 , т.е.
, т.е. .
. получаем
получаем .
. для любой случайной величины
для любой случайной величины 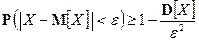 .
. , а дисперсия
, а дисперсия  . В силу неравенства Чебышёва искомая вероятность
. В силу неравенства Чебышёва искомая вероятность . ■
. ■ .
. ? Оценить эту вероятность, пользуясь неравенством Чебышёва.
? Оценить эту вероятность, пользуясь неравенством Чебышёва.
 .
.
 .
.

 .
. .
. .
. . Согласно неравенству Чебышёва оценка снизу этой вероятности
. Согласно неравенству Чебышёва оценка снизу этой вероятности  .
. ? Оценить эту вероятность, пользуясь неравенством Чебышёва.
? Оценить эту вероятность, пользуясь неравенством Чебышёва.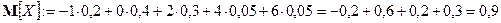 .
.
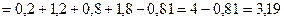 .
.

 .
. .
. .
. . Согласно неравенству Чебышёва оценка снизу этой вероятности
. Согласно неравенству Чебышёва оценка снизу этой вероятности  .
. , а дисперсия
, а дисперсия  . Требуется оценить снизу вероятность
. Требуется оценить снизу вероятность 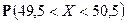 . Так как неравенство
. Так как неравенство ,
, . Согласно неравенству Чебышёва
. Согласно неравенству Чебышёва .
. .
.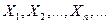 - последовательность независимых случайных величин, имеющих дисперсии, которые ограничены одной и той же постоянной
- последовательность независимых случайных величин, имеющих дисперсии, которые ограничены одной и той же постоянной  . Тогда, каково бы ни было постоянное положительное число
. Тогда, каково бы ни было постоянное положительное число  , имеет место обобщённое неравенство Чебышёва
, имеет место обобщённое неравенство Чебышёва .
. - продолжительность горения электролампы, взятой из
- продолжительность горения электролампы, взятой из  . Очевидно, что средняя продолжительность горения ламп в выборке
. Очевидно, что средняя продолжительность горения ламп в выборке ,
, .
. .
.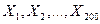 - независимые случайные величины, то эта вероятность оценивается снизу правой частью обобщённого неравенства Чебышёва, где следует положить
- независимые случайные величины, то эта вероятность оценивается снизу правой частью обобщённого неравенства Чебышёва, где следует положить  ,
,  ,
,  .
. . ■
. ■ .
. , чтобы с вероятностью, не меньшей 0,95, можно было утверждать, что среднее арифметическое значение этих измерений отличается от
, чтобы с вероятностью, не меньшей 0,95, можно было утверждать, что среднее арифметическое значение этих измерений отличается от  , а дисперсия
, а дисперсия  . Поэтому
. Поэтому .
. .
. ,
, ,
,  . Тогда требуемое неравенство во всяком случае будет выполняться, если:
. Тогда требуемое неравенство во всяком случае будет выполняться, если: . ■
. ■ .
.