 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| РАСЧЕТ ЛИНИИ С ДВУСТОРОННИМ ПИТАНИЕМ.
Рассмотрим методику расчета линий с двусторонним питанием, являющуюся общим случаем расчета простых замкнутых сетей, поскольку, кольцевая сеть легко приводится к схеме двустороннего питания. Схема такой сети для трех нагрузок изображена на рис. 7-4. Здесь s1,s2 и s3 — нагрузки в точках 1, 2 и 3;S1, S2, S3 и S4 — полные мощности на участках линии; Z0-1, Z1-2, Z2-3 и Z3-4, l1, l2, l3, и l4 — соответственно полные сопротивления и длины участков; А и В — источники питания; UA и UB — напряжения источников питания.
Рис. 7-4. Схема сети с двусторонним питанием. Падение линейного напряжения на любом участке линии между нагрузками
где Ii — ток на данном участке; Zi — сопротивление этого участка. Поскольку
где Ui — сопряженный вектор напряжения в данной точке сети. Полагая вектор Ui ориентированным по вещественной оси, получим:
где Si и Ui взяты для одной и той же точки участка. Вектор напряжения Ui изменяется вдоль линии по мере удаления от источника питания. Однако, пренебрегая потерями мощности в линии, т. е. исходя из постоянства напряжения вдоль каждого участка и полагая U1 = U2 = ... = UN (что для сетей местного значения вполне допустимо), можем на основании второго закона Кирхгофа написать следующее равенство для падений напряжения между точками А и В:
где Uн — номинальное напряжение сети. Одновременно, пользуясь первым законом Кирхгофа для точек 1, 2, 3 и исходя из принятого допущения об отсутствии потерь мощности в сети, можно составить следующие равенства:
Подставив эти выражения в уравнение (8-1), получим:
Отсюда искомая мощность, выходящая в линию из пункта А, будет
Обозначив сопротивления от пункта В до нагрузок1, 2, 3 соответственно черезZ1, Z2 и Z3, а полное сопротивление линии между пунктами A и В через Zabи подставив эти величины в формулу (8-3), получим:
или в общем виде для многих нагрузок:
Аналогичную формулу можно вывести и для нагрузки, идущей из пунктаВ:
гдеZ’i — сопротивления от пункта А до каждой нагрузки. Остальные нагрузки по участкам, знаяZi', легко найти, пользуясь выражениями (8-2), а так как на схеме рис. 7-4 за положительное направление мощностей было условно принято направление от А к В, то часть нагрузок на участках, прилегающих к источнику питания В, получится с отрицательным знаком, что будет указывать на их обратное направление. В некоторой точке окажется, что мощности к ней притекают с двух сторон. В данном случае такой точкой является точка 2. Эта точка называется точкой раздела и обычно обозначается значком 6 . Второй член в выражении (8-4) представляет собой уравнительную мощность, протекающую по линии АВ вследствие разности напряжений между этими пунктами. Эта мощность не зависит от нагрузок линии, так как она будет иметь место и при s1, s2, … sN. При равенстве напряжений в точках питания или при кольцевой схеме (когда точки А и В совмещены) UA =UB. Второй член в правой части равенства (8-4) пропадает, и формула для определения мощности, выходящей из пункта А, принимает вид:
При расчете местных сетей обычно пользуются формулой (8-5), считая напряжения источников питания одинаковыми. Таким образом, для того чтобы определить мощность, выходящую из одного источника питания, необходимо определить сумму моментов нагрузок относительно другого источника и разделить ее на полное сопротивление всего участка сети с двусторонним питанием. При одинаковых напряжениях на источниках питания или при расчете кольцевых схем падение напряжения от обоих источников питания до точки раздела одинаково. Поэтому в этой точке сеть может быть условно разрезана и потери напряжения определены для любой из половин как для сети с односторонним питанием. Чтобы определить с помощью полученных выше формул, как распределяются мощности в линиях с двусторонним питанием, в общем случае подсчет производят в комплексной форме:
В некоторых случаях расчеты можно упростить, перейдя к раздельному определению распределения активной и реактивной мощностей и заменив в формуле (8-5) сопротивление Zabсоответствующей проводимостью:
Подставив эти величины в формулу (8-5), получим:
Произведя все действия и разделив вещественные и мнимые члены, получим:
Формулы (8-6) позволяют вести подсчет в отдельности для активной и реактивной нагрузок, пользуясь абсолютными значениями вещественных и мнимых составляющих нагрузок и сопротивлений. Эти формулы можно использовать для расчета потокораспределения в сетях двустороннего питания и с разными уровнями напряжения источников питания. Однако в этом случае на полученный по формулам (8-6) результат потокораспределения необходимо наложить уравнительную мощность, рассчитанную по второму члену выражения (8-4). В случае, если напряжения источников питания совпадают по фазе, уравнительная мощность, протекающая от одного источника питания к другому, будет
Необходимость в подобных расчетах возникает тогда, когда в целях перераспределения реактивной мощности для оптимального использования линий замкнутой сети на одном из источников питания устанавливают вольтодобавочные автотрансформаторы. Определив, как в линии двустороннего питания распределяются нагрузки, переходят к подсчету потерь напряжения обычным способом. 10 Регулирование напряжения изменением параметров сети Из зависимостей (19) и (20) видно, что в незначительных пределах напряжение можно регулировать изменением активного и реактивного сопротивлений питающей сети. При нескольких параллельно работающих линиях или трансформаторах (рис. 11, а, б) в часы минимальной нагрузки, когда снижаются потери напряжения, можно отключить одну из линий или трансформатор, что приведет к увеличению потерь напряжения в питающей сети и, следовательно, к понижению напряжения у потребителя. 6 Линия с двусторонним питанием при различающихся напряжениях по концам относится к числу электрических цепей с независимыми источниками мощности. Для расчета таких линий используется принцип наложения. На рисунке 4.8 приведена исходная схема линии с двусторонним питанием (а) при U
Рисунок 4.8 Токи в исходной схеме рассматриваются как результат суммирования двух систем токов, одна из которых определяется действием напряжений Если предположить для схемы рисунка 4.8 б, что напряжение в точке 1 и 2 равно номинальному, то для расчета этой схемы можно использовать формулы, полученные для кольцевой сети. При расчете схемы рисунка 4.8в нагрузки узловых точек 1 и 2 можно исключить из схемы (токи в ветвях не потекут), а в линии будет протекать только уравнительный ток, вызванный действием подключенной DЕ
В результате наложения двух расчетов получаем мощности на головных участках линии
В общем случае при n нагрузках с учетом (4.29) эти формулы могут быть записаны в виде
Дальнейший расчет заключается в определении точки потокораздела и в определении напряжений в узловых точках, так же как и в кольцевых сетях.
5. Батареи статических конденсаторов (БСК) используются для следующих целей: компенсация реактивной мощности в сети, регулирование уровня напряжения на шинах, выравнивание формы кривой напряжения в схемах управления с тиристорным регулированием. Передача реактивной мощности по линии электропередачи приводит к снижению напряжения, особенно заметному на воздушных линиях электропередачи, имеющих большое реактивное сопротивление. Кроме того, дополнительный ток, протекающий по линии, приводит к росту потерь электроэнергии. Если активную мощность нужно передавать именно такой величины, которая требуется потребителю, то реактивную можно сгенерировать на месте потребления. Для этого и служат конденсаторные батареи. Наиболее распространенными видами компенсирующих устройств, которые выполняют роль местных генераторов реактивной мощности на предприятиях, являются батареи статических конденсаторов и синхронные двигатели. Конденсаторные батареи устанавливают на цеховых общезаводских трансформаторных подстанциях — со стороны низкого или высокого напряжения. Чем ближе компенсирующее устройство к приемникам реактивной энергии, тем больше звеньев системы электроснабжения разгружается от реактивных токов. Однако при централизованной компенсации, т. е. при установке конденсаторов на трансформаторных подстанциях, конденсаторная мощность используется более полно. Мощность конденсаторных батарей может быть определена по диаграмме рис. 1.
Рис. 1. Диаграмма мощностей Qк = P1 х tgφ1 - P2 х tgφ2, где P1 и P2 - нагрузка до и после компенсации, φ1 и φ2 - соответствующие углы сдвига фаз. Реактивная мощность, отдаваемая компенсирующей установкой, Q = Q1 - Q2, где Q1 и Q2 — реактивная мощность до и после компенсации. Активная мощность, потребляемая из сети компенсирующим устройством Рк = Р2 - Р1. Величину необходимой мощности конденсаторной батареи можно определить приближенно без учета потерь в конденсаторах, которые составляют 0,003 - 0,0045 кВт/квар Qк = P (tgφ1 - tgφ2) Пример расчета и выбор конденсаторных батарей для компенсации реактивной мощности Необходимо определить номинальную мощность Qк конденсаторной батареи, необходимой для повышения коэффициента мощности до значения 0,95 на предприятии с трехсменным равномерным графиком нагрузки. Среднесуточный расход электроэнергии Аа = 9200 кВтч; Ар = 7400 кварч. Конденсаторы установлены на напряжение 380 В. Среднесуточная нагрузка Pср = Аа/24 = 9200/24 = 384 кВт. Мощность конденсаторных батарей Qк = P (tgφ1 - tgφ2) = 384 (0,8 - 0,32) = 185 квар, где tgφ1 = Ар/Аа = 7400/9200 = 0,8, tgφ2 = (1 - 0,952)/0,95 = 0,32 Выбираем трехфазные конденсаторы типа KM1-0,38-13 каждый номинальной мощностью 13 квар на напряжение 380 В. Число конденсаторов в батарее n = Q/13 = 185/13 = 14 Мощность различных конденсаторных установок для среднесуточной нагрузки можно найти в электротехнических справочниках и каталогах производителей.
4 Послеаварийный режим связан со значительным отклонением частоты и может возникнуть при аварийном расчленении объединенной энергосистемы на части, как с недостатком, так и избытком активной мощности. Наиболее опасным является понижение частоты. При возникновении дефицита мощности и резком снижении частоты в результате первичного и вторичного регулирования все станции окажутся полностью загруженными. Если отключившаяся в результате аварии мощность генераторов больше, чем был резерв на всех станциях системы, то частота не восстановится до номинальной. При значительном дефиците мощности снижение частоты будет большим. Для предотвращения лавины частоты должны быть приняты автоматические быстродействующие меры. Восстановление частоты осуществляют путем автоматической частотной разгрузки (АЧР), при которой отключается часть потребителей. Преднамеренное отключение части потребителей позволяет сохранить в работе генерирующие мощности, обеспечить электроснабжение остальных нагрузок. Рассмотрим процесс изменения частоты при действии АЧР (рис. 16.14). Здесь РГС – частотная характеристика генерирующей части системы, а Рн – статическая характеристика нагрузки. Рассмотрим случай, когда энергосистема работает без резерва с нагрузкой РГС0 и частота равна номинальной.
ΔРГ. Тогда характеристика генерирующей части системы сместится в положение РГС1, и частота в соответствии со статической характеристикой нагрузки снизится до f1 (точка 2). Для увеличения частоты до номинальной следует отключить с помощью АЧР часть нагрузки потребителей: ΔРАЧР = ΔРГ. На рис. 16.14 это выражено переносом статической характеристики нагрузки параллельно самой себе в положение Рн1. При таком отключении мощность генерирования станет больше мощности потребления, и частота будет восстанавливаться по прямой 3–4. В точке 4 установится номинальная частота при новой генерирующей и потребляемой мощности. Для того чтобы при снижении частоты не было лишних отключений всю систему АЧР разбивают на две категории (АЧР I и АЧР II), каждая из которых выполняется в виде нескольких очередей. В АЧР I и II очереди отличаются одна от другой только установками по частоте. При снижении частоты происходит отключение потребителей от первой очереди АЧР I. Если частота продолжает снижаться, то срабатывает вторая очередь АЧР I с меньшей уставкой по частоте и т. д. Такая «самонастраивающаяся» система АЧР обеспечивает отключение мощности потребителей, равной возникшему дефициту мощности. При таком подходе подключение потребителей к АЧР допустимо производить с запасом, не боясь излишних отключений. Если после действия АЧР I частота не восстановится, то с выдержками времени вступают в действие очереди АЧР II и дополнительно отключаются потребители. Изменение частоты во времени при возникновении дефицита активной мощности и действии АЧР показано на рис. 16.15. Точка 0 кривой а характеризует начальный момент времени, в который возник дефицит мощности. При этом происходит снижение частоты по кривой а. В точке 1 частота f достигает уставки первой очереди АЧР-I, и происходит отключение части потребителей. Если при этом еще сохранился некоторый дефицит мощности, то будет происходить дальнейшее снижение частоты.
В точке 2 при частоте f2 происходит дополнительное отключение потребителей от второй очереди АЧР-I. Избирательное действие АЧР с учетом возникновения величины и места дефицита мощности осуществляется путем учета скорости изменения частоты в местной (МЭС) и объединенной (ОЭС) энергосистемах. Из-за меньшей инерции в местной энергосистеме скорость изменения частоты всегда больше, чем в объединенной системе (кривая б на рис. 16.15). Другими словами, изменение частоты происходит тем быстрее, чем больше дефицит мощности. Поэтому при выпадении одной и той же мощности в местной и объединенной системе скорость изменения частоты будет выше в местной энергосистеме. Таким образом, для выравнивания частоты при отключении межсистемной линии в МЭС, кроме устройств АЧРОЭС, выполняемых по условию работы ОЭС, необходимо устройство АЧРМЭС, реагирующее на значение частоты и скорость ее изменения. В ОЭС при регулировании частоты возникает ряд особенностей, которые обусловлены наличием межсистемных связей и большой мощностью объединения. Если межсистемные линии имеют значительную пропускную способность, то объединение нескольких систем фактически является одной системой, и отличий, характерных для межсистемных линий, нет. Однако в большинстве случаев межсистемные линии электропередачи имеют ограниченную пропускную способность либо при большой пропускной способности предназначены для передачи больших потоков мощностей из одной системы в другую. Такой режим работы обычно диктуется экономическими соображениями, когда осуществляется транзит дешевой энергии от ГЭС или от экономичной ТЭС. В процессе регулирования частоты в энергосистеме изменяются потоки активной мощности по межсистемным линиям электропередачи и может наступить их перегрузка.
на рис. 16.16.
При малых отклонениях частоты изменение этого потока незначительно. В послеаварийных режимах, когда происходит значительное снижение частоты, непропорциональное изменение нагрузки потребителей отдельных систем может привести к перегрузке межсистемных линий и их отключению, что разовьет аварию. Поэтому во избежание неприятностей, связанных с перегрузкой межсистемных линий, в процессе регулирования частоты осуществляют контроль за перетоками мощности по линиям. В объединенных международных энергосистемах на межсистемных линиях электропередачи задаются графики обменных потоков мощности в соответствии с интересами каждой страны. Регулирование частоты поручается энергосистеме одной из стран, входящих в объединение. Другие энергосистемы изменяют мощности своих станций так, чтобы выдерживать заданные перетоки по межсистемным линиям. 8Для определения наиболее выгодного варианта электрической сети применили метод приведенных затрат. Приведенные затраты З определяются из соотношения:
где рн – нормативный коэффициент эффективности, равный 0,12 К – капиталовложения определяются по укрупненным показателям стоимости электрооборудования и сооружения воздушных линий. Суммарные капиталовложения по электрической сети определяются:
где
Годовые эксплуатационные расходы определяются по формуле:
где Состоят из амортизационных отчислений подстанций и линий электропередач:
где
Определяются по формуле (3.7):
где
где
Более экономичным считается вариант с наименьшими приведенными затратами. При разнице приведенных затрат в пределах 5%, варианты считаются экономически равноценными, поэтому следует выбрать вариант более надежный, удобный для эксплуатации в различных режимах работы, перспективный для дальнейшего развития и т.д.
|








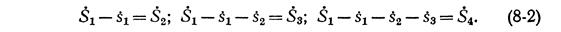






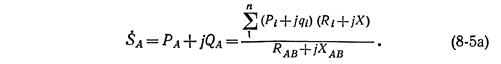






 (26)
(26)
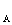 ¹U
¹U  , а также две схемы, полученные в соответствии с принципом наложения (б,в). При этом в напряжении на шинах В выделены две составляющие, одна из которых равна напряжению на шинах А, т.е.
, а также две схемы, полученные в соответствии с принципом наложения (б,в). При этом в напряжении на шинах В выделены две составляющие, одна из которых равна напряжению на шинах А, т.е. =
=  +D
+D  (4.28)
(4.28)
 =
=  =
=  . (4.29)
. (4.29) ,
, .
. , (4.30)
, (4.30) . (4.31)
. (4.31)
 Этот режим характеризуется точкой 1, в которой РГС0 = Рн. Предположим теперь, что в результате аварии отключена генерирующая мощность
Этот режим характеризуется точкой 1, в которой РГС0 = Рн. Предположим теперь, что в результате аварии отключена генерирующая мощность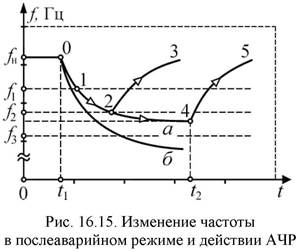
 Поясним причины возможной перегрузки на примере схемы объединенной энергосистемы, представленной
Поясним причины возможной перегрузки на примере схемы объединенной энергосистемы, представленной Пусть поток мощности при номинальной частоте направлен из системы 1 в систему 2. Статические (частотные) характеристики систем генерирования имеют крутизну k1ГС и k2ГС, причем klГС > k2ГС (рис. 16.17). Тогда при снижении частоты с fн до f1 в процессе первичного регулирования мощность станции энергосистемы 1 увеличится на ΔP1, а мощность станций системы 2 – на ΔP2, причем ΔP1 > ΔP1. При этом поток мощности по межсистемной линии увеличится, что может привести к ее перегрузке.
Пусть поток мощности при номинальной частоте направлен из системы 1 в систему 2. Статические (частотные) характеристики систем генерирования имеют крутизну k1ГС и k2ГС, причем klГС > k2ГС (рис. 16.17). Тогда при снижении частоты с fн до f1 в процессе первичного регулирования мощность станции энергосистемы 1 увеличится на ΔP1, а мощность станций системы 2 – на ΔP2, причем ΔP1 > ΔP1. При этом поток мощности по межсистемной линии увеличится, что может привести к ее перегрузке. (3.1)
(3.1) (3.2)
(3.2) - капиталовложения на сооружение подстанций, тыс. тг.
- капиталовложения на сооружение подстанций, тыс. тг. - капиталовложения на сооружение воздушных линий, тыс. тг.
- капиталовложения на сооружение воздушных линий, тыс. тг. (3.3)
(3.3) - ежегодные отчисления на амортизацию электрооборудования, тыс.тг.
- ежегодные отчисления на амортизацию электрооборудования, тыс.тг. (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) и
и  - нормы ежегодных отчислений на амортизацию, %.
- нормы ежегодных отчислений на амортизацию, %. - ежегодные отчисления на ремонт и обслуживание, тыс.тг.
- ежегодные отчисления на ремонт и обслуживание, тыс.тг.
 и
и  - нормы ежегодных отчислений на ремонт и обслуживание ЛЭП, %.
- нормы ежегодных отчислений на ремонт и обслуживание ЛЭП, %. - стоимость годовых потерь электроэнергии, тыс.тг. Определяются по формуле
- стоимость годовых потерь электроэнергии, тыс.тг. Определяются по формуле (3.8)
(3.8) - стоимость 1-го кВт∙ч, потерь электроэнергии, тг/кВт∙ч
- стоимость 1-го кВт∙ч, потерь электроэнергии, тг/кВт∙ч ,
,  - годовые потери в линиях электропередач кВт∙ч.
- годовые потери в линиях электропередач кВт∙ч.