 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Статистические модели в виде нелинейных полиномов.
Параболическая регрессия.
Коэффициенты регрессии определяем по методу наименьших квадратов.

Приравняем к нулю частные производные функции по коэффициентам b0, b1, b2.
Выполнив преобразования, получим систему линейных уравнений с тремя неизвестными (b0, b1,b2).
Введем обозначения:
(18)
С учетом принятых обозначений система будет иметь следующий вид:
Определим неизвестные коэффициенты b0, b1, b2.
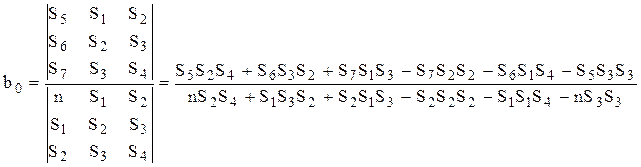

 . . После решения системы уравнений и вычисления коэффициентов b0, b1, b2 проводится статистический анализ полученного уравнения регрессии. Аналогичным образом будут определяться коэффициенты параболы любого порядка. Исследование уравнения проводится по статистическим критериям. Однако в этом случае не требуется вычислять выборочные коэффициенты корреляции. Адекватности уравнения регрессии эксперименту можно добиться, повышая степень полинома. Однако при этом все коэффициенты следует вычислять заново, так как существует корреляция между коэффициентами. Экспериментальная часть. Задание № 5.
Определить зависмость теплоемкости воды и гексана от температуры.
Исходные данные:
Объем выборки N=8.
Для описания зависимости теплоемкости кислорода от температуры выберем полином второго порядка:
В результате расчетов, выполненных по программе, были получены следующие значения коэффициентов регрессии: b0=24,62708333 b1=0,047055357 b2=-1,88512E-05 Коэффициент парной корреляции рассчитываем по формуле (4) или (5). В результате уравнение регрессии будет иметь вид:
Результаты расчета представлены в табл. 1.
Среднеквадратическое отклонение рассчитывается по формуле
Величина ошибки S =2,13172 показывает, что расчетные значения достаточно хорошо совпадают с экспериментальными, а, следовательно, зависимость теплоемкости воды от температуры можно описать полиномом второго порядка. Значение коэффициента парной корреляции равно rxy =0,995164. .
Для описания зависимости теплоемкости бутана от температуры выберем полином второго порядка:
В результате расчетов, выполненных по программе, были получены следующие значения коэффициентов регрессии: b0=8,308; b1=0,5097; b2= -0,00018878 . Коэффициент парной корреляции рассчитываем по формуле (4) или (5). В результате уравнение регрессии будет иметь вид:
Результаты расчета представлены в табл. 1.
Среднеквадратическое отклонение рассчитывается по формуле:
Величина ошибки S =49,94045 показывает, что расчетные значения достаточно хорошо совпадают с экспериментальными, а, следовательно, зависимость теплоемкости бутана от температуры можно описать полиномом второго порядка. Значение коэффициента парной корреляции равно rxy =0,989608. . |




 (16)
(16) (17)
(17) ;
;  ;
;  ;
;  ;
; ;
;  ;
;  .
.

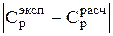
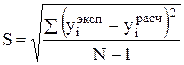 ,
,









