 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Итоговая контрольная работа
Итоговая контрольная работа По алгебре и началам анализа за курс 11 кл. (2012 - 2013 уч. год) Учитель: Тюлюкина О.А. ВАРИАНТ 1. Часть I. 1. Укажите наименьшее значение функции у = 2 – 5sin x. Ответ: 2. Найдите производную функции у = 2х + cos х. 1) у 2) у 3.
4.
5.
Итоговая контрольная работа По алгебре и началам анализа за курс 11 кл. (2012 - 2013 уч. год) Учитель: Тюлюкина О.А. ВАРИАНТ 2. Часть I. 1. Укажите наибольшее значение функции у = - 3 – 2cos x. Ответ: 2. Найдите производную функции у = е – х + х2. 1) у 2) у 3.
4.
5.
Часть II. Запишите обоснованное решение и ответ. 1. Найдите первообразную F(x) функции f(x) = 2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых. 3. Тело движется прямолинейно по закону х(t) = 2t4 - 3t3 – 5t2 (x в метрах, t в секундах). Найдите его скорость в момент времени t = 10c. 4. Касательная к графику функции f(x) = 2x3 – 3x2 – 4 параллельна прямой у = 12х + 1. Найдите абсциссу точки касания. 5. Дана функция f(x) = 8x2 – x4 . Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [-1; 3] .
6. Найдите площадь фигуры, ограниченной графиком функции f(x) = -x2 + 6x - 5, прямыми х = 2, х = 3 и осью абсцисс, изобразив рисунок.
7. Найдите все решения уравнения cos 2x + sin x = cos2 x, принадлежащие отрезку [0; 2π].
Вариант 2. Часть II. Запишите обоснованное решение и ответ. 1. Найдите первообразную F(x) функции f(x) = ех – 2 + 4х, если график первообразной проходит через точку М(2; -10). 2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых. 3. Тело движется прямолинейно по закону х(t) = 3t4 - 2t3 +1 (x в метрах, t в секундах). Найдите его скорость в момент времени t = 2. 4. Угловой коэффициент касательной к графику функции f(x) = 7x2 – 2x + 1 равен 26. Найдите абсциссу точки касания.
5. Дана функция f(x) = x3 - 3x2 + 4. Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [0; 4] .
6. Найдите площадь фигуры, ограниченной графиком функции f(x) = x2 – 6x + 10, прямыми х = -1, х = 3 и осью абсцисс, изобразив рисунок.
7. Найдите все решения уравнения cos 2x + sin2 x = cos x, принадлежащие отрезку [-π; π].
Вариант 1. Итоговая контрольная работа |



 = 2х – sin x 3) у
= 2х – sin x 3) у 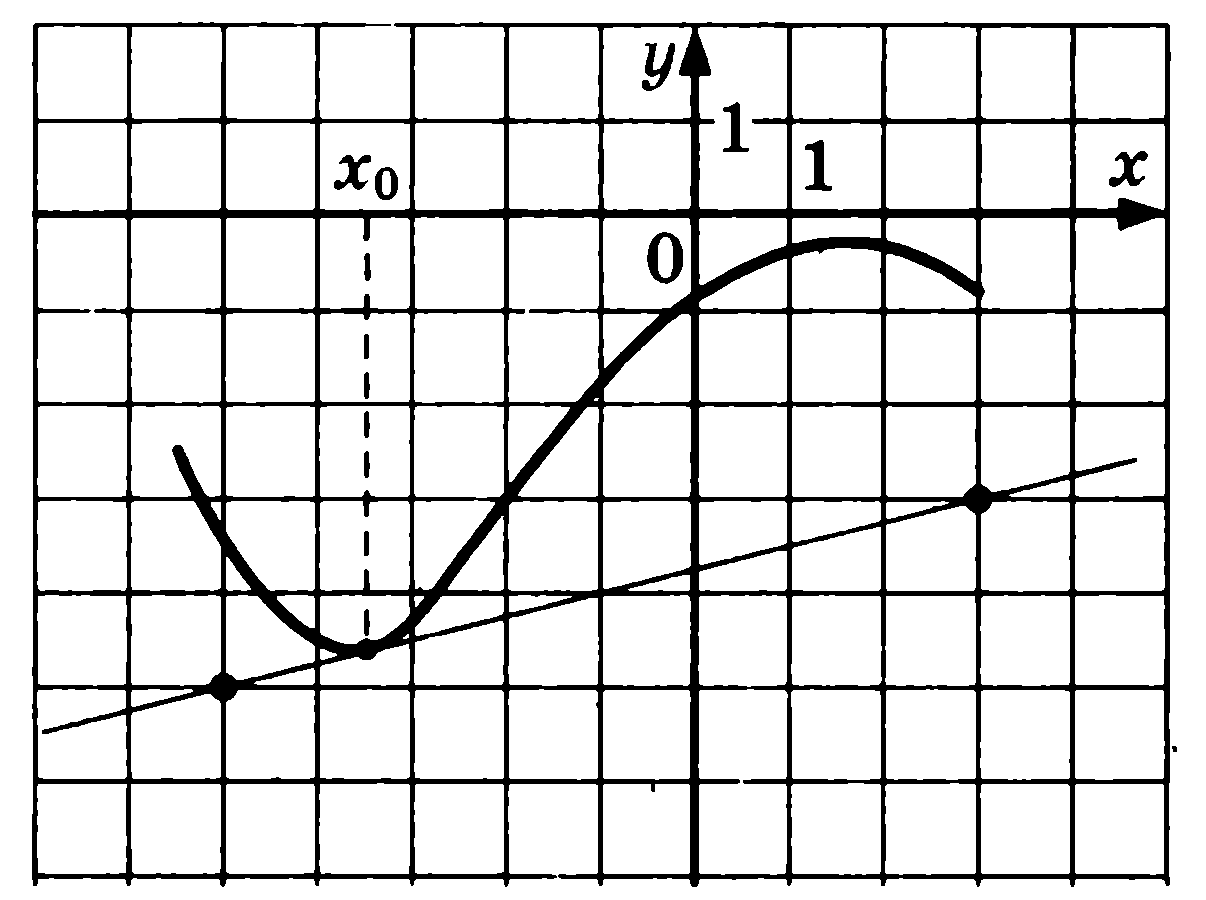




 + 2х, если график первообразной проходит через точку М(3; 13).
+ 2х, если график первообразной проходит через точку М(3; 13).