 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Уравнения с разделяющимися переменными
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 16 По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ Наименование работы: РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ, ЛИНЕЙНЫХ ОДНОРОДНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 1-ГО ПОРЯДКА.
Для специальности 230111, 230115.
Составлено преподавателем Калмыковой О.И.
г. Смоленск 2012 г. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 16 По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ (2 курс) Наименование работы: РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ, ЛИНЕЙНЫХ ОДНОРОДНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 1-ГО ПОРЯДКА.
1. Цель работы:Приобретение навыков решения дифференциальных уравнений 1-го порядка с разделяющимися переменными. Приобретение практических навыков решения линейных дифференциальных уравнений 1-го порядка, приведение дифференциальных уравнений к виду линейного относительно y и 2. Литература: 2.1. Н.В. Богомолов "Практические занятия по математике" гл.15 §1, М.: Высшая школа, 1990 г. 2.2. В.А. Подольский, А.М. Суходольский "Сборник задач по математике" гл.15 §1,2 М.: Высшая школа, 1978 г. 3. Подготовка к работе: 3.1. Изучить теоретический материал по теме “Решение дифференциальных уравнений 1-го порядка с разделяющимися переменными. Решение однородных дифференциальных уравнений 1-го порядка”. 3.2. Подготовить бланки отчета. 3.3. Подготовить ответы на вопросы допуска к работе: 3.3.1. Дать понятие дифференциального уравнения 1-го порядка. 3.3.2. Понятие дифференциального уравнения n-го порядка. 3.3.3. Понятие общего решения дифференциального уравнения n-го порядка. 4. Основное оборудование: 4.1. Литература, конспект. 5. Задание: Найти общее решение (общий интеграл) дифференциального уравнения. 6. Порядок выполнения работы: 6.1. Записать задание своего варианта в отчет. 6.2. Решить дифференциальные уравнения 1-го порядка с разделяющимися переменными. 6.3. Записать ответы, оформить отчет 6.4. Подготовить ответы на контрольные вопросы. 7. Содержание отчета: 7.1. Титульный лист. 7.2. Цель работы. 7.3. Результаты и ход выполнения работы. 7.4. Выводы отчеты. 8. Контрольные вопросы: 8.1. Дать понятие дифференциального уравнения 1-го порядка. 8.2. Понятие дифференциального уравнения n-го порядка. 8.3. Понятие общего решения дифференциального уравнения n-го порядка. 8.4. От чего зависит порядок дифференциального уравнения? 8.5. Понятие и общий вид однородного дифференциального уравнения 1-го порядка. 8.6. Алгоритм решения дифференциального уравнения. 9. Приложение:
10. Методические указания: Обыкновенные дифференциальные уравнения.
Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков. В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки. Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.
Тогда получаем:
Определение. Дифференциальным уравнениемназывается уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных. Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Пример.
Определение. Общим решениемдифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество. Свойства общего решения. 1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = j(х, С0).
Определение. Решение вида у = j(х, С0) называется частным решениемдифференциального уравнения.
Определение. Задачей Коши(Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка) Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную Определение. Интеграломдифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.
Пример. Найти общее решение дифференциального уравнения
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
Теперь интегрируем:
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
Определение. Интегральной кривойназывается график y = j(x) решения дифференциального уравнения на плоскости ХОY. Дифференциальные уравнения первого порядка.
Определение. Дифференциальным уравнением первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде:
- это так называемая дифференциальная формауравнения первого порядка.
Рассмотрим подробнее типы уравнений первого порядка и методы их решения.
Уравнения с разделяющимися переменными
Определение.Уравнение вида: Метод решения
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными. Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Пример. Найти общее решение дифференциального уравнения:
- это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.
Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.
Пример. Найти решение дифференциального уравнения
при у(2) = 1 получаем Итого:
Проверка:
Пример. Решить уравнение
Пример. Решить уравнение
Если у(1) = 0, то
Итак, частный интеграл: ОДНОРОДНЫЕ УРАВНЕНИЯ. Уравнение вида y'= f (y/x) (1) называется однородным уравнением. Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой y= ux, где u – новая функция. Дифференцируя равенство y= ux, получим dy/dx=x*du/dx+u Подставив y и dy/dx в уравнение (1), получим x*du/dx + u= f (u), откуда du/ f ( u) – u = dx/x (2) Это уравнение с разделяющимися переменными u и x. Найдя общее решение(интеграл) уравнения (2) и заменив u на y/x, получим общее решение (интеграл) данного однородного уравнения. ПРИМЕР: Найти общий интеграл уравнения (xy + y2) dx – (2x2 + xy) dy = 0 Решение: Разрешим данное уравнение относительно производной:
Поделив числитель и знаменатель правой части уравнения на x2, получим y' = Таким образом, y' есть функция отношения y/x, т.е. данное уравнение – однородное. Введем теперь новую функцию u= y/x. Тогда y= ux и y'=
Откуда
Интегрируя это уравнение, получим ln |x| = - u – 2ln |u| - ln C, или u = - ln |Cxu2|, откуда Cxu2 = e-u Заменяя в последнем равенстве u отношением y/x, окончательно находим общий интеграл данного уравнения : y2 =Cxe-y/x .
|



 .
. 2)
2)  3)
3) 
 2)
2)  3)
3) 
 2)
2)  3)
3) 
 2)
2)  3)
3) 
 2)
2)  3)
3) 
 2)
2)  3)
3) 


 - уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
- уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t). - обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается
- обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается  .
. - обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается
- обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается 
 - дифференциальное уравнение в частных производных первого порядка.
- дифференциальное уравнение в частных производных первого порядка. , то какова бы не была точка (х0, у0) в области D, существует единственное решение
, то какова бы не была точка (х0, у0) в области D, существует единственное решение  уравнения
уравнения  .
.







 - это общее решение исходного дифференциального уравнения.
- это общее решение исходного дифференциального уравнения.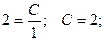


 тогда при подстановке в полученное выше уравнение имеем:
тогда при подстановке в полученное выше уравнение имеем:
 называется уравнением с разделяющими переменными, где правая часть уравнения есть произведение функций, каждая из которых зависит только от одного элемента.
называется уравнением с разделяющими переменными, где правая часть уравнения есть произведение функций, каждая из которых зависит только от одного элемента.



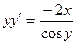



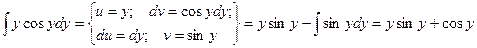

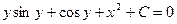

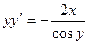 - верно
- верно при условии у(2) = 1.
при условии у(2) = 1.





 или
или  - частное решение;
- частное решение; , итого
, итого - верно.
- верно.




 - общий интеграл
- общий интеграл - общее решение
- общее решение при условии у(1) = 0.
при условии у(1) = 0.






 .
.
 (*)
(*)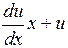 . Уравнение (*) преобразуется в уравнение с разделяющимися переменными :
. Уравнение (*) преобразуется в уравнение с разделяющимися переменными : ,
,