 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Решение дифференциальных уравнений
Решение систем линейных алгебраических уравнений Решение систем линейных алгебраических уравнений (СЛАУ) является наиболее распространенной подзадачей при решении многих инженерных задач. СЛАУ может быть задана в форме
или в общем виде
Часто используется матричная форма записи A×x = b ,(3) где x= А=
Существуют два типа методов численного решения СЛАУ - прямые и итерационные. Прямые методы основаны на приведении систем общего вида к специальной форме - диагональной, треугольной и т.п., позволяющей достаточно просто получить решение. Прямые методы требуют для получения решения (или заключения об отсутствии решения) выполнения точно определенного числа действий, зависящего только от порядка системы и структуры матрицы коэффициентов при неизвестных. Прямые численные методы позволяют получить точное решение при отсутствии ошибок округления. Наиболее распространенный метод данного типа - метод Гаусса последовательного исключения неизвестных. Итерационные методы позволяют найти с заданной точностью лишь приближенное решение системы путем последовательного построения приближений (итераций), начиная с некоторого заданного пользователем начального приближения. Нельзя заранее определить число необходимых операций. Наиболее распространенным является метод ускоренной итерации (Зейделя). Говорят, что итерационный процесс сходится, если последовательность получаемых в ходе расчета приближений монотонно стремится к точному решению системы. В процессе расчета последовательность новых приближений не всегда сходится к решению системы! Задание Решить систему уравнений с помощью пакета Mathcad при заданном преподавателем варианте: n =5
Порядок выполнения 1. В свободном поле ввел имя матрицы и знак присвоения A:= 2. Нажал клавишу "Векторные и матричные операции" на панели инструментов, в появившейся панели выбрала "Создать матрицу или вектор", задал размер матрицы 3x3 и ввел значения элементов в соответствии с заданием.
2. Решение систем нелинейных алгебраических уравнений Системы нелинейных уравнений представляют в виде приравненной нулю вектор-функции
Решение систем нелинейных уравнений выполняют численными итерационными методами. Широко распространен метод последовательных приближений, который можно использовать, если элементы вектор-функции
Алгоритм решения в принципе совпадает с алгоритмом решения СЛАУ методом ускоренной итерации. В большинстве современных промышленных программ, предназначенных для решения технологических задач электроэнергетики, используют различные модификации метода Ньютона. Метод Ньютона Дано уравнение f(x)=0. Известно, что на участке [a, b] имеется один корень, требуется его уточнить. На рис.1 показана функция y = f(x) Возьмем некоторую точку x0 участка [a,b] и проведем в точке [x0,f(x0)] графика касательную к нему. Уравнение касательной имеет вид: f(x0)/( x0- x1 ) = f’(x0). В качестве первого приближения корня уравнения f(x)=0 примем абсциссу точки пересечения касательной с осью 0x. x1 = x0 - f’(x0)/ f(x0) Полученное значение можно использовать для дальнейшего уточнения коня, при этом i-тое приближение xi = xi-1 - f’(xi-1)/ f(xi-1). Процесс повторяют до тех пор, пока f(xi) не станет с заданной точностью (e) равно нулю f(xi)£e, или уточнение корня станет незначительным, т.е. f’(xi-1)/ f(xi-1) £e. Остается решить вопрос о выборе точки интервала, из которой следует проводить касательную. Приближенное значение корня, полученное методом Ньютона, лежит в интервале [a, b] если знак функции совпадает со знаком второй производной, т.е. f(x0)*f’’(x0)>0. Так, в нашем примере видно, что f(x0) > 0 и f’’(x0)>0, ибо кривая вогнута. Задание Решить систему нелинейных уравнений с помощью пакета Mathcad при заданном преподавателем варианте -5 из таблицы 1 имеем:
Порядок выполнения 1. Задал начальные приближения корней заданной системы уравнений
2. Написал слово «дано» - Given и после этого ввел заданную систему уравнений
3. Написал слово «найти» - find и в скобках указал значения каких переменных следует найти. После этого поставил знак равенства и получил четыре результата.
Решение дифференциальных уравнений Метод численного интегрирования Эйлера предназначен для решения задачи Коши: найти на интервале времени tÎ[T0,T] решение дифференциального уравнения
при заданных начальных условиях: В результате решения данной задачи получают в форме графика или таблицы значения функции y(t). Метод Эйлера является дискретным, т.е. таким, посредством которого вычисляется последовательность приближенных значений Геометрическая интерпретация численного интегрирования методом Эйлера приведена на рис. 1.
Рис. 2. Участок искомой неизвестной функции y(t) “заменяют” касательной к нему прямой (линеаризация функции в окрестности заданной точки). По известным значениям y0, h и вычисленному значению производной, определяющей наклон касательной, можно из треугольника ABC определить значение приращенияфункции Dy0 = y1 – y0 =h f(y0,Ò0) на отрезке времени длины h. Тогда значение y1 для момента времени t1 =T0+h можно определить по формуле
Полученное значение можно использовать для вычисления по аналогичной формуле значения функции в точке t2=T0+2h=t1+h и т.д. пока не будет достигнут конец заданного интервала интегрирования. В общем случае расчетная формула метода Эйлера имеет вид
Очевидно, что чем меньше величина h, тем ближе полученное значение yk+1 к точному значению неизвестного точного решения y(tk+1). Абсолютная погрешность выполнения шага численного интегрирования не может быть определена, известно лишь что она для данного метода прямо пропорциональна величине h. В связи с этим разработаны различные процедуры получения оценки локальной погрешности на шаге численного интегрирования, требующие, очевидно, увеличения объема вычислений. Наиболее простая, достаточно надежная, но не очень эффективная с точки зрения вычислительных затрат процедура оценки точности расчета заключается в следующем: 1.Выполняют один шаг интегрирования величины h , получают значение yk+1 для t=t k+1. 2. Из той же начальной точки выполняют два шага интегрирования и определяют значение 3.По разности двух значений, полученных с абсолютной погрешностью, отличающейся вдвое, можно вычислить приближенную оценку D локальной погрешности на k-ом шаге интегрирования:
где p - порядок точности метода численного интегрирования, для метода Эйлера p=1. 4.Если оценка локальной погрешности D больше, чем желаемая пользователем точность расчета e, то величину шага интегрирования необходимо уменьшить и продолжить расчет с новым значением h . Очевидно, что неудачный шаг должен быть повторен из той же исходной точки. Иногда для определения приемлемого значения h необходимо выполнить 2¸3 подобных итерации. Для выбора величины шага можно использовать формулу
где a - коэффициент запаса, значение которого обычно выбирают из диапазона значений 0.5¸ 0..9. Эту формулу полезно использовать на каждом шаге и в том случае, когда текущая оценка погрешности удовлетворяет заданной точности. При этом возможно будет рекомендовано большее значение h, что позволит сократить общее число необходимых шагов интегрирования. В случае решения систем дифференциальных уравнений вычисления выполняются по аналогичным формулам. Однако выбор шага осуществляют по наибольшему значению оценки погрешности D. Задание
Список литературы 1. Синегубов А.П. Методические указания к практическим занятиям по курсу “Вычислительные методы в энергетике”/ ДГТУ, 2014, 18с. |



 (1)
(1)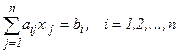 .(2)
.(2) -вектор искомых неизвестных размерности n;
-вектор искомых неизвестных размерности n; - матрица коэффициентов при неизвестных размерности n´n;
- матрица коэффициентов при неизвестных размерности n´n;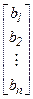 - вектор свободных членов СЛАУ размерности n.
- вектор свободных членов СЛАУ размерности n. .
. .
.






 =0. (4)
=0. (4) можно привести к виду
можно привести к виду . (5)
. (5)

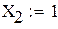



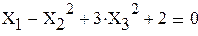

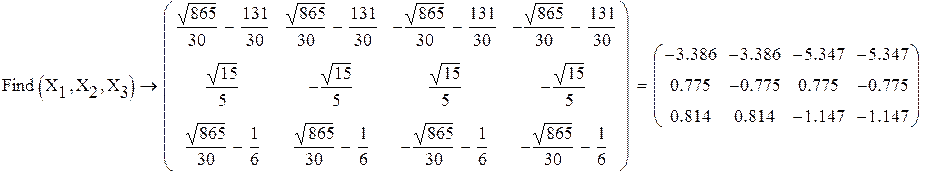




 (6)
(6) t(0)=T0 , y(0)=y0.
t(0)=T0 , y(0)=y0. на множестве точек tk+1=tk+h , k=0,1,2..., принадлежащих заданному интервалу времени. Здесь h - заданная пользователем величина шага численного интегрирования.
на множестве точек tk+1=tk+h , k=0,1,2..., принадлежащих заданному интервалу времени. Здесь h - заданная пользователем величина шага численного интегрирования.
 . (7)
. (7) . (8)
. (8) для момента времени t=t k+1.
для момента времени t=t k+1.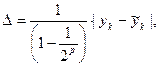 (9)
(9) , (10)
, (10)