 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Домашнее задание и допуск к выполнению лабораторной работы
1 Изучить основные понятия и определения, теоретический материал. 2 Изучить лабораторную установку, схему лабораторных испытаний. 3 Изучить порядок выполнения лабораторной работы. 4 Изучить технику безопасности при выполнении лабораторной работы. 5 Ответить на контрольные вопросы для подготовки к допуску к выполнению лабораторной работы. 4 Порядок выполнения лабораторной работы. метрологическое Исследование методов регулирования производительности центробежного вентилятора заключается в задании различных режимов его работы, в измерении координат и в обработке экспериментальных данных. Измерение координат центробежного вентилятора производится с помощью стационарных и переносных электроизмерительных и других приборов. В лабораторной установке измеряются следующие электрические, механические и аэродинамические параметры: а) напряжение, ток и активная мощность, потребляемая электродвигателем вентилятора из сети; б) скорость вращения исследуемого центробежного вентилятора; в) давление и скорость воздуха на выходе нагнетательного патрубка; К расчетным координатам исследуемого центробежного вентилятора относятся следующие параметры: а) механическая мощность, подводимая к центробежному вентилятору для создания воздушного потока с заданными параметрами; б) снижение потребляемой электрической мощности при регулировании производительности вентилятора изменением скорости вращения. в) полезная механическая мощность центробежного вентилятора, затрачиваемая на создание воздушного потока с заданными параметрами; г) коэффициент полезного действия электродвигателя вентилятора; д) статический КПД центробежного вентилятора при изменении скорости вращения при постоянных значениях аэродинамического сопротивления воздуховодов. д) расчет погрешности экспериментальных данных и результатов обработки экс-периментов по формулам (9) и (11). Выполнение лабораторной работы проводится в следующей последовательности: а) изучение конструкции и принципа действия лабораторной установки; б) изучение конструкции и принципа действие центробежного вентилятора; в) выполнение экспериментов и снятие экспериментальных данных. Эксперименты проводятся для 5-ти значений аэродинамического сопротивления центробежного вентилятора и для 5-ти значений скорости вращения; г) построение напорных характеристик центробежного вентилятора и воздухопровода по экспериментальным данным; д) расчет мощности электродвигателя, потребляемой из сети, мощности, подводимой к вентилятору, и снижение потребляемой электрической мощности при регулировании производительности вентилятора изменением скорости вращения; е) расчет полезной мощности, затрачиваемой вентилятором на создание воздушного потока с заданными параметрами; ж) построение графиков зависимости коэффициента полезного действия электродвигателя и статического КПД вентилятора в зависимости от скорости вращения при фиксированных значениях аэродинамического сопротивления воздуховодов. Результаты измерений можно представить в следующем виде
где ∆x – погрешность измерений. Точно определить величину погрешности невозможно, так как она носит случайный характер. Иначе можно было бы найденную погрешность ввести в результат измерения и получить истинное значение xист. Задачей математической статистики является наилучшая оценка результата xист и нахождение пределов интервала (3) по результатам измерений. Точно определить величину погрешности невозможно, так как она носит случайный характер. Иначе можно было бы найденную погрешность ввести в результат измерения и получить истинное значение xист. Задачей математической статистики является наилучшая оценка результата xист и нахождение пределов интервала (8) по результатам измерений. Если проведено n измерений величины x, то среднее арифметическое значение принимается за лучшую оценку истинного результата измерений
где xi – результат i-го измерения. Средняя квадратичная погрешность определяется по формуле
где n – число измерений. Важно знать, насколько может отличаться от истинного значения x среднее арифметическое, полученное по формуле (10) для n повторных равноточных измерений. Из теории видно, что средняя квадратичная погрешность среднего арифметического S равна средней квадратичной погрешности каждого результата измерений Sn, деленного на корень из числа измерений n
Вероятность того, что результат измерений отличается от истинного на величину, не большую, чем ∆x обозначим через α. Вероятность α называется доверительной вероятностью, а интервал значений измеряемой величины от -∆x до +∆x называется доверительным интервалом. Определим доверительный интервал. Чем большим он будет установлен, тем более вероятно, что xист окажется в этом интервале. Но широкий интервал дает меньшее представление относительно величины xист. При учете только случайных погрешностей и при небольшом числе измерений n для уровня доверительной вероятности α полуширина доверительного интервала равна
где tα,n – коэффициент Стьюдента (таблица 1). Таблица 1 – Коэффициент Стьюдента
Для окончательной установки границы доверительного интервала необходимо расширить его с учетом систематической погрешности ∆xсист. Систематическая погрешность, как правило, указана в паспорте или на шкале прибора, а в некоторых случаях может быть принята равной половине цены деления младшего разряда шкалы. Суммарная погрешность (абсолютная) определяется как корень квадратный из суммы квадратов случайной и систематической погрешностей:
Относительная погрешность определяется как
Выражение (13) позволяет оценить величину погрешности по отношению к самой измеряемой величине, измеряется в процентах. При обработке результатов прямых измерений предлагается следующий порядок операций. 1 Вычисляется среднее значение из n измерений по формуле (17). 2 По формуле (10) определяется среднеквадратичная погрешность среднего арифметического значения. 3 Задается доверительная вероятность α и определяется коэффициент Стьюдента tα,n для заданного α и числа произведенных измерений n по таблице 2. 4 По формуле (12) находится полуширина доверительного интервала (абсолютная погрешность результата измерений). 5 Оценивается относительная погрешность результата измерений по формуле (14). 6 Окончательный результат записывается в виде
|



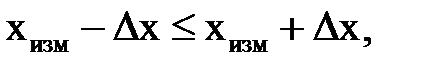 (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) (13)
(13) (14)
(14) (15)
(15)