 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задача № 1 Обработка прямых однократных измерений 12
В результате однократного измерения получено значение диаметра цилиндра D. Определить относительную погрешность измерения диаметра D. Конечный результат однократного измерения диаметра цилиндра D для доверительной вероятности α =1 записать в виде: Х = (Хср ± Δ) мм; εх = … %; α =1. Исходные данные для решения задачи № 1 приведены в табл. 3. Таблица 3 - Исходные данные для задачи № 1
Решение: Относительную погрешность измерения диаметра вычисляем по формуле
где εD - относительная погрешность измерения; ΔD - абсолютная погрешность измерения; D - значение диаметра цилиндра.
Конечный результат однократного измерения диаметра цилиндра для доверительной вероятности α =1 записываем в виде: D = (95 ± 0,2) мм; εD = 0,2%; α =1. Ответ: D = (95 ± 0,2) мм; εD = 0,2%; α =1.
Задача № 2. Обработка прямых многократных измерений При измерении сопротивления резистора с 8-кратным наблюдением параметра получены результаты, приведённые в таблице. Исключит грубые промахи. Считая систематическую погрешность отсутствующей, определить результат измерения сопротивления резистора с доверительной вероятностью Рдов. Таблица 4 - Исходные данные для задачи № 2
Решение: 1. Рассчитываем среднее арифметическое значение по формуле
2. Находим оценку среднеквадратического отклонения (СКО) результата измерения по формуле
3. Рассчитать доверительный интервал случайной погрешности (случайную погрешность) по формуле
где tα,n - коэффициент Стъюдента. Из табл. 1 для n = 8 выбираем значение коэффициента Стьюдента
4. Определяем абсолютную погрешность Δt измерения с учетом случайной Δ и инструментальной Δиt погрешностей по формуле
5. По формуле вычисляем относительную погрешность
6. Окончательный результат измерения записываем в виде: R = (162.5 ± 3,36) Ом; εt =2,1%; α=0,95. Ответ: R = (162.5 ± 3,36) Ом; εt =2,1%; α=0,95.
Задача №3. Обработка косвенных измерений при воспроизводимых условиях Площадь (объём) геометрического тела определяется на основании измерений (выполненных с известной точностью) его параметров с последующим вычислением по соответствующей эмпирической формуле. Определить результат косвенного измерения площади (объёма) предложенных геометрических тел. Таблица 5 - Исходные данные для задачи № 3
Решение: Допустим, что некоторая функция является результатом умножения двух величин где а, h- прямо измеренные величины: а=(60±1) мм; εR= 1,67%; α = 1; h = (10±1) мм; εh= 10,0%; α = 1. Значение измеряемой величины согласно выражению Для расчета погрешностей функции V воспользуемся следующим способом: 1) вначале определим абсолютную погрешность по формуле
2) Пересчитаем относительные погрешности величин a, h к доверительной вероятности α = 0,95:
Абсолютную погрешность определяем по формуле
Результат измерения с учетом правил представления результатов измерений записываем в виде: V = (360000±24300) мм3; εV=6.75%; α = 0,95. Ответ: V = (360000±24300) мм3; εV=6.75%; α = 0,95..
Задача № 4. Проведено косвенное измерение напряжения на известном сопротивлении R с помощью амперметра: а) Чему равно искомое напряжение? Таблица 6 - Исходные данные для задачи № 4
Решение: По формуле где R, I - прямо измеренные величины: R= (100±5) мм; εR= 5%; α = 1; I = (100±5) мм; εh= 5%; α = 1. Значение измеряемой величины согласно выражению Для расчета погрешностей функции l воспользуемся следующим способом: 1) вначале определим абсолютную погрешность по формуле
2) Пересчитаем относительные погрешности величин a,b к доверительной вероятности α = 0,95:
Абсолютную погрешность определяем по формуле
Результат измерения с учетом правил представления результатов измерений записываем в виде: U = (10±0.471) В; εU=4,71%; α = 0,95. Ответ: U = (10±0.471) В; εU=4,71%; α = 0,95.
Задача № 5 При косвенном определении плотности сплава масса сплава оказалась равной m, г. Цена деления при определении массы равна 1 г. Объём исследуемого вещества V известен с погрешностью ± 1 см3. Чему равна плотность идентифицируемого материала? Записать результат измерения плотности с учётом погрешности косвенных измерений.
Решение: Расчет плотности материала проводим по формуле Масса образца получена взвешиванием на весах с инструментальной погрешностью Δm=Δиm= 1г m = (456±1.0) г; εm=0.22%; α = 1 Объем образца получен прямым измерением с помощью мензурки с инструментальной погрешностью ΔV= ΔиV=1 см3, V = (200±1.0) см3; εV=0.5%; α = 1 По формуле определяем плотность материала
По формуле получаем расчетное соотношение для относительной погрешности измерения плотности
Пересчитаем относительные погрешности величин m, V к доверительной вероятности 0,95:
Абсолютную погрешность плотности определяем по формуле
Результат измерения с учетом правил представления результатов измерений записываем в виде ρ = (2,28±0,82) г/см3; εm=36,2%; α = 0,95 Ответ: ρ = (2,28±0,82) г/см3; εm=36,2%; α = 0,95
Список использованной литературы 1. Никифоров А.Д. Метрология, стандартизация и сертификация. Уч.пособие/ А.Д. Никифоров, Т.А. Бакиев. – 2-е изд., испр. М.: Высшая школа, 2003. 2. Эрастов В.Е. Метрология, стандартизация и сертификация: учебн. пособие. –М.: ФОРУМ, 2008. 3. Сергеев А.Г. Метрология, стандартизация и сертификация: учебное пособие. –М.: Логос, 2004.
12 |





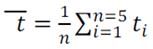
 Ом
Ом
 Ом
Ом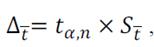
 Ом
Ом
 Ом
Ом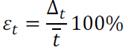



 мм3
мм3

 %
%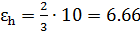 %
% %
%
 мм3
мм3
 В
В
 %
% %
% %
% В
В
 г/см3
г/см3


 %
% %
% %
%
 г/см3
г/см3