 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Симпсон формуласы (парабола формуласы)
Лекциялар курсы
Шымкент 2009 г.
K85 ӘОЖ 518.517.392+800.92
Құрақбаев Д. С. «Сандық әдістер» пәнінең лекциялар курсы. –Шымкент: OҚМУ, -2009. –111б. Берілген оқу - әдістемелік нұсқауда «Сандық әдістер» курсынан типтік есептерді шешуге қажетті теориялық мағлұматтар мен формулалар келтірілген. Жоғарыда айтылғандарды ескере отырып, оқу - әдістемелік құралды барлық техникалық және технологиялық мамандықтардың күндізгі және сыртқы бөлім студенттерінің қолдануларына болады деп есептеймін.
Пiкiр жазғандар: Н.Е. Ержанов – Қ.А.Яссауи атындағы ХҚТУ ШБ-нің, «Есептеу техникасы және бағдарламалау» кафедрасының меңгерушісі, ф-м.ғ.к., доцент У. М. Ибрагимов - M.Әуезов атындагы ОҚМУ-нің «Информатика» кафедрасының доцентi .
М.Әуезов атындағы ОҚМУ – нің әдістемелік Кеңесімен қаралып, баспаға ұсынған. Хаттама №2. 30.11.2008ж.
© М.Әуезов атындағы Оңтүстік Қазақстан мемлекеттік университеті
МАЗМҰНЫ 1 Қателіктер теориясының бастапқы ұғымдары........................ ..............5 1.1 Абсолютті және салыстырмалы қателіктер......…………….………...5 1.2 Қателіктердің негізгі пайда себептері………………….......................6 1.3 Қателіктің жалпы формуласы................................................................7 2 Алгебралық және трансцендент тендеулерді жуықтап шешу әдістері. Кiрiспе………………………………….………………………8 2.1 Алгебралық және трансцендент тендеулер......…………………… …8 2.2 Түбірлерді бөлектеу...………………………………………………….10 2.3 Аралықты қақ бөлу әдісі....……………………………………………12 2.4 Хордалар әдісі...………………………………………………………..14 2.5 Жанамалар әдісі ..……………………………………………………...17 2.6 Қосалқы әдісі..…………………………………………………………20 2.7 Біртіндеп жақындау әдісі...…………………………………….……..21 3 Сызықты тендеулер жүйелерін шешу әдістерінің жалпы cипаттамасы…………………………………………………………..22 3.1 Жүйелерді кері матрица көмегімен шешу. Крамер формуласы…....23 3.2 Гаусс әдісі……………………………………………………………...25 3.3 Басты элементтер әдісі……………………………………………….31 3.4 Гаусс әдісін анықтауыштарды есептеуде қолдану…………………32 3.5 Гаусс әдісімен кері матрицаны есептеу……………………………..34 3.6 Квадрат түбірлер әдісі………………………………………………..36 3.7 Итерация әдісі…………………………………………………………37 3.8 Зейдель әдісі …………………………………………………………..38 4 Фукцияларды жуықтату (интерполяциялау). Интерполяциялық полиномдар…………………………………………………………….…41 4.1 Жуықтату есебінің қойылуы…………………………………………....41 4.2 Орталық айырымдар кестесі. Гаусс, Стирлинг және Бессель интерполяциялық формулалары…………………………………………45 4.3 Гаусстің интерполяциялық формулалары……………………………..45 4.4 Стирлингтің интерполяциялық формуласы……………………………47 4.5 Бесселдің интерполяциялық формуласы………………………………48 4.6 Лагранждың интерполяциялық формуласы…………………………....49 5 Анықталған интегралдарды жуықтап есептеу әдістері............................................ ………………………………………..51 Кіріспе…………………………………………………...............................51 5.1 Сандық интегралдаудың қарапайым формулалары…………………....51 5.1.1 Тіктөртбұрыштар формуласы…………………………….....................51 5.1.2 Трапеция формуласы…………………………………………........…..53 5.1.3 Симпсон формуласы (параболалар формуласы)……………..............54 5.2 Интерполяциялық квадратуралар алдын-ала түйіні берілген квадратуралық формулалар…………………………………………….......57 5.2.1 Лежандр көпмүшелері және Гаусс формуласы……….......................57 5.2.2 А.А.Марковтың квадратуралық формуласы………………...............64 5.3 Тең коэффициентті квадратуралық формулалар…………………..….76 5.3.1 Түйіндерді табу…………………………………...………......….........76 5.3.2 Тұрақты салмақты функциялы интегралдар. Чебышевтің квадратуралық формуласы….............................................................……78 6 Жай дифференциалдық теңдеулерді жуықтап шешу………………….82 6.1 Коши есебі. Жалпы қарастыру..……………….…………………….....82 6.2 Анықталмаған коэффициенттер әдісі...………………………………..83 6.3 Жай дифференциалдық теңдеулерді Эйлер әдісімен шешу…………..85 6.4 Бірінші ретті жай дифференциалдық тендеулерді Рунге-Кутта әдісімен шешу…………………………………………….....89 6.5 Жай дифференциалдық теңдеулер үшін шекті-айырымдар есебі. Есептің қойылу шарты…………………………………………………....89 6.6 Айырымдық тор және торлық функциялар…………………………....90 6.7 Екінші ретті сызықтық дифференциалдық теңдеулерді шешу үшін шекті-айырымдар әдісі……………………………………...91 6.8 Қуалау әдісі……………………………………………………………...93 6.9 Төртінші ретті жай дифференциалдық теңдеулерді торлар әдісімен шешу…………………………………………………....98 6.9.1 Балка теңдеулерінің жалпы түрлері………………………………....98 6.9.2 Негізі серпілмелі балканың иілуін есептеу……………...………….100 7 Интегралдық тендеулерді шешу.................................................................108 7.1.1 Квадратуралар әдісі..............................................................................109 Әдебиеттер.......................................................................................................111
Лекция 1. Жуықтап есептеу. Сандардың абсолютті және салыстырмалы қателігі. Қателіктің негізгі түбірі. Дұрыс цифрлар саны. Бір және бірнеше айнымалылары функциясының абсолютті және салыстырмалы қателіктері.Қосындының, айырымның, туындының, дербес көрсеткіштің, түбірдің қателіктері. 1 Қателіктер теориясының бастапқы үғымдары. 1.1 Абсолютті және салыстырмалы қателітер. Санның жуық мәні деп сол санның дәл мәнінен айырмашылығы өте аз шаманы айтады. Практикада санның дәл мәні белгісіз болғандықтан оның жуық мәні пайдаланылады. Мысалы,өте жиі кездесетін Жуық шаманың қателігі деп оның сәйкес деп шамадан айырмасын айтады. Яғни, а және А арқылы жуық және дәл шамаларды белгілесек, онда қателік былайша анықталады:
Көп жағдайда қателіктің таңбасы белгісіз болады(өйткені дәл шаманың өзі белгісіз). Сондықтан қателіктің абсолютті мәнін біген ыңғайлы. Анықтама 1.Қателіктің абсолютті мәнін абсолютті қателік деп атайды. Яғни,
Мысалы, Кейде абсолютті қателік белгісіз болғандықтан оның орнына шектелген абсолютті қателік үғымын пайдаланған ыңғайлы. Анықтама 2.Абсолютті қателіктен кіші емес кез келген шаманы абсолютті қателік деп атайды. Сонымен, егер
Бүдан мынадай тұжырым жасауға болады: санның дәл мәні мына шектерде жатады а- Анықтама 3.Абсолютті қателіктің берілген санның дәл мәнінің модуліне қатнасы салыстырмалы қателік деп аталады. Яғни,
Санның дәлмәні А көп жағдайда белгісіз болғандықтан салыстырмалы қателіктері былай да анықтайды:
Шектік абсолюттік қателік сияқты, шектик Жуық санның салыстырмалы қателігі осы дұрыс цифрлардың санымен процент арқылы өрнектеледі. Мәселен а – ның құрамында бір ғана дұрыс цифр болса, онда А санының салыстырмалы қателігі сол саның 10% - іие тең екеу болса –1% - іие, ал үшеу болса 0.1% - іие т.с.с. Доңгелектеу қателіктері. Доңгелектеу амалы деп жуық санның құрамынан бір немесе бірнеше ондық цифрларды алып тастауды айтады. Ол мынадай ерекше байланысты жүзеге асыралады: егер оң жағында алып тасталынғалы тұрған цифр 5 – тен кіші болса, онда сол цифрдың сол жағындағы көрші цифрдың сан мәні сақталады, а кері жағдайда (яғни 5ке – тең, не 5 – тен үлкен) оның мәні бірге арттырылады. Мәселен 5,3726
1.2 Қателіктердің негізгі пайда болу себептері
Математикалық есептеулерде кездесетін қателіктерді бірнеше группаға бөлуге болады. Олардың арасындағы ең бастылары мыналар: 1. Математикалық есептің қойылуына байланысты пайда болатын қателіктер. Әдетте табиғи құбылыстарды математикалық әдістермен зерттеуді оңайлату үшін әртүрлі шарттар қабылдауға мәжбүр боламыз. Осыдан келіп қателіктер пайда болады. 2. Шексіз проценттерге байланысты пайда болатың қателіктер (шектер, қатарлар және т.б.). Шексіз процестерді аяғына дейін орындауға болмайтындықтан қатардың белгілі бір мүшесінде тоқтауға тура келеді. 3. Жуық шамалармен амалдар орындағанда пайда болатын қателіктер. Ары қарай осы үшінші группаға жататын қателіктерді қарастырамыз. Теорема 1. Бірнеше жуық шамалардың алгебралық қосындысының абсолютті қателігі осы шамалардың абсолютті қателіктерінің қосындысынан аспайды. Дәлелдеу: х1, х2, ..., хn – жуық шамалар болсын. Осы шамалардың алгебралық қосындысын қарастырайық U = онда
Яғни, Салдар. 2 – ші анықтама бойынша алгебралық қосындысының абсолютті қателігі ретінде мына шаманы алуға болады
Теорема 2. Жуық шамалардың көбейтіндісінің қатысты қателігі осы шамалардың қатысы қателіктерінің қосындысынан аспайды. Яғни, U = х1 . х2 . ... . хn, болса, онда Теорема 3. Жуық шамалардың бөліндісінің қатысты қателіктерінің қосындысынан аспайды. Яғни, u = x/y болса, онда Теорема 4. Егер u = xk болса, онда Теорема 5. Егер u = 1.3 Қателіктің жалпы формуласы Қателіктер теориясының негізгі мақсаты мынада: берілген жуық шамалардың қателіктері белгілі, осы шамалардың функциясының қателігін табу керек. Функция u = f(x1, x2, …., xn) берілсін,
Көп жағдайда
Шектелген салыстырмалы қателіктің формуласын былайша жазуға болады:
Бақлау сұрақтар мен жаттығулар 1. Абсолют және салыстырмалы қателіктер қалай есептеледі? 2. Сенімді цифрлар қалай есептеледі? 3. Қателікті есепке алу нені білдіреді? 4. Қателіктердің пайда болуының негізгі көздерін атаңыз. Әдебіеттер Демидович Б.П., Марон И.А. Основы вычислительной математики. С.17-52. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. С.9-21 Лекция 2.Алгебралық және трансценденттік теңдеулерді жуықтап шешу.Есептің қойылу шарты. Түбірлерді айыру. Теңдеудің графикалық шешімі. Жартылай 2-ге бөлу әдісі. 2 Алгебралық және трансцендент тендеулерді жуықтап шешу әдістері Кіріспе Бұл жұмыста f(x)=0 түріндегі теңдеулерді шешудің түрліше сандық әдістері қарастырылады, мұндағы f(x)-кез-келген функция. Кейбір жекелеген жағдайларда ғана көрсетілген теңдеудің «дәлң шешімін анықтауға болады, бірақ, бұл кезде алынатын формулалар әдетте өте көлемді болып келеді, сондықтан оларды қолдану едәуір қиындықтар туғызады. Егер алгебралық немесе трансцендентті теңдеулер айтарлықтай күрделі болса, онда олардың дәл шешімдерін табу өте қиынға соғады. Сонымен қатар, кейбір жағдайларда теңдеулердің тек жуық коэффициенттері белгілі болады, және, сәйкесінше, теңдеудің дәл шешімдері туралы мәселенің маңызы жойылады. Аталған жағдайларға байланысты қарастырылатын теңдеудің түбірлерін жуықтап табудың әдістері және олардың дәлдік дәрежесін бағалау әдістерінің маңыздылығы арта түседі. Төменде алгебралық және трансцендентті теңдеулерді шешуге арналған келесі сандық әдістер баяндалады: түбірлерді ажырату, теңдей екіге бөлу әдісі, хорда әдісі, жанамалар әдісі (Нъютон әдісі), аралас әдіс және итерация әдісі. Ұсынылып отырған жұмыс студенттердің, технологтардың және ғылыми қызметкерлердің т.б. жұмысын жеңілдету және уақытты тиімді пайдалану үшін қажет. Осы тақырыптарға байланысты берілген типтік есептерді шығару үшін технологтар, ғылыми қызметкерлер және студенттер, біріншіден осы әдістердің әрқайсысына программа құруы қажет. Екіншіден осы құрылған программаларды компьютерлерге енгізіп, содан кейін жауабын алады. Бұл көп уақытты алады. Осы жерде мына құрылған комплекс программа арқылы студенттер өзінің теңдеуін берілгендерін енгізіп, қалаған әдіс бойынша теңдеудің жауабын ала алады. Ұсынып отырған жұмыс бірнеше тақырыптарға бөлінген. Әрбір тақырып есеп шығаруға қажетті негізгі программалар мен блок схемалардан, формулалармен теорияларды баяндаудан басаталады. Одан соң программаларды біріктіріп, кез келген теңдей берілген кезде жауап алынатын программа, соңында мысал, программа, блок схема берілген. Аталған әдістер үшін FoxPro ортасында алгоритмдер және программалар құрылған. 2.1 Алгебралық және трансцендент теңдеулер. Бір айнымалысы бар кез келген теңдеуді
түрінде жазуға болады. Мұндағы Анықтама: Анықтама:Егер (1) теңдеудегі
онда (1) теңдеуді алгебралық теңдеу деп атаймыз. Мұндағы Алгебралық теңдеулерге мысалдар келтіреміз: x2-5x+6=0;
Көрсетілген мысалдарда екінші және үшінші теңдеулерді қарапайым арифметикалық амалдармен теңдеуге келтіруге болады. Егер (1) теңдеудегі x+5 tgx = 0; 2x-2cosx = 0; lg(x+1) = tg(x); (1) теңдеудің түбірі нақты комплекс сан болуы мүмкін. Біз жеке қана нақты түбірлерді анықтаймыз. Теңдеуді жуықтап шешу екі кезеңнен тұрады: 1. 2. Әр интервалдағы нақты түбірлерді жуықтап шешу әдісімен берілген дәлдікпен есептеп табамыз. Төменде жоғары алгебра курсыдағы теңдеулердің кейбір қасиеттерін дәлелдеусіз келтіреміз: 1. Кез келген алгебралық теңдеудің кемінде бір нақты немесе комплекс түбірі болады. 2. Кез келген n-дәрежелі алгебралық теңдеудің түбірлерінің саны n- нен артық болмайды. 3. Кез келген нақты коэфицентті алгебралық теңдеу тек қана жұп комплекс түбірге ие болуы мүмкін. 4. Кез келген тақ дәрежелі алгебралық теңдеу кемінде бір нақты түбірге ие болады. Теңдеулер бірінші және екінші дәрежелі болса (сызықты және квадрат теңдеулер), онда дайын есептеу формулалары бар, олар бізге мектеп программасынан белгілі. Теңдеулер үшінші және төртінші дәрежелі болғанда да дайын формулалар көмегімен есептеуге болады (Кардано формулалары). Бірақ та бұл формулалар күрделі. Алгебралық теңдеулердің бес және одан көп болған кезде оларды аналитикалық жолмен шешу мүмкін емес (Абель формуласы). Мұндай теңдеулерді тек қана дербес жағдайларда шешуге болады. Сондықтан да сандық әдістерде түбірлерді жуықтап табудың бірнеше әдістері қолданылады. Бұл әдістермен кез келген алгабралық немесе трансцендент теңдеулер берілген дәлдікпен шешіледі.
2.2 Түбірлерді бөлектеу. Түбірлерді бөлектеу дегеніміз теңдеудің тек қана бір ғана түбірі жататын [а,b] интервалын табу. Бұл интервалда f(х) функциясы монотонды және екі ұшында қарама-қарсы таңбалы мәндер қабылдауға тиіс, яғни f(а)f(b)<0 және f(х), f’(х) – таңбаларын өзгертпейді. Түбірлерді графикалық және аналитикалық әдістермен бөлектеуге болады.
1. Түбірлерді графикалық әдіспен бөлектеу. 1 – тәсіл. Бұл тәсіл өте қарапайым, былай орындалады. Декарттың координата системасында у= f(х) функция графигін саламыз. Графиктің ОХ осімен қиылысқан нүктелер теңдеудің түбірлері болып табылады. Мысал: х3 – 3х2 + 1=0 теңдеудің түбірлері 1- суретте бөлектелген.
Сурет 1 2 – тәсіл. f(х)=0 теңдеуді f1(х)= f2(х) түріне келтіреміз. Декарттың координата системасында у= f1(х) және у= f2(х) функцияларының графиктерін саламыз. Егер осы қисық сызықтар қиылысатын болса, онда қиылысу нүктелерінен ОХ осіне перпендикуляр жүргіземіз. Перпендикуляр сызықтың ОХ осімен қиылысу нүктесі теңдеудің түбірі болады. 2- суретте жоғарыдағы мысал осы тәсілмен шешіп көрсетілген.
Сурет 2
Теңдеулердің түбірін жуықтап табудың ең қарапайым әдісі ретінде графикалық әдіс есептеледі. Бұл әдіспен теңдеулердің түбірлерін жоғары дәлдікпен табу үшін графиктерді мүмкіншілігі барынша анық және үлкен масштабпен сызу керек. Сонда да графикалық әдіспен түбірлерді жоғары дәлдікпен табу қиын. Өйткені сызбада теңдеудің түбірлерін тек қана шекараланған аралықта іздейміз, яғни қалағанымызша үлкен аралық ала алмаймыз және теңдеудің неше түбірі бар деген сұраққа жауап бере алмаймыз. Сондықтан да түбірлерді жоғары дәлдікпен табу үшін, басқа жуықтау әдістерін қолданамыз. Ал графикалық әдісті түбірлерді бөлектеуде пайдаланамыз.
2. Түбірлерді аналитикалық әдіспен бөлектеу:
Теорема 1: Егер
Теорема 2: Егер
Теорема 3: Егер
Теорема 4: Егер
Анықтама: у=
Осы айтылғандардан пайдаланып у=х3–3х2+1=0 теңдеуінің түбірлерін бөлектейміз. Ол үшін функцияның туындысын 0-ге теңеп, критикалық нүктелерін табамыз.
Енді әрбір аралықтар үшін у=
]- ]0;2[ функциясы кемиді ; ]2; [-1;0]; [0;1] ; [2;3] аралықтарында у = f(х) функциясының түбірлері жатады.
Түбірлерді есептеу.
Анықтама: Егер Анықтама: Әрбір итерациядан кейін есептелген түбір нақты түбірге жуықтайтын болса, онда итерациялық процесс ықшамдалатын, ал жуықтамаса ықшамдалмайтын процесс деп аталады. Әрбір итерациядан кейін мына шарт тексерілуі тиіс:
мұндағы х(і+1) - (і+1) – итерацияда есептелген түбір, х(і) - і- итерацияда есептелген түбір. Бұл шарт итерация процесстің аяқталу шарты деп аталады.
2.3 Аралықты қақ бөлу әдісі.
Мысал:
Есептеуді бастаймыз
Сондықтан
Бақлау сұрақтар мен жаттығулар 1. Теңдеу түбірлерін бөлу әдістері? 2. Қақ бөлу әдісінің жинақталу шарты? 3. Түбірлерді бөлуге арналған алгоритмді құру әдістері? 4. Қақ бөлуге арналған алгоритмді құру әдістері? Әдебіеттер Демидович Б.П., Марон И.А. Основы вычислительной математики. С.112-119. Мысовских И.П. Ликции по методам вычислений. С.7 - 71 Лекция 3.Алгебралық және трансценденттік теңдеулерді жуықтап шешу.Есептің қойылу шарты. Түбірлерді айыру. Хорда, жанама, жай итерация және комбинацияланған әдіс
2.4 Хордалар әдісі Трансцендент және алгебралық теңдеулерді шешуде хордалар әдісі көп қолданылады. Сонымен 1 - жағдай:
өрнектері орынды. Осылардың біреуін а) нұсқасын көріп шығайық.
формуласымен өрнектеледі. Жүргізілген хорданың ОХ өсінің қиылысу нүктесі х1 –ді жуық түбір деп аламыз және оның координатасын анықтаймыз. (4) теңдеуге х=x1 және y=0 мәндерін қойып‚ х1 –ді есептейміз‚ яғни
Егер табылған түбір х1 (3) – шартты қанағаттандырса‚ онда х1 –ді
Егер
формуламен‚ 2 - жағдай: Онда өрнектері орынды. Осылардың біреуін көріп шығайық.
Хорданың ОХ өсімен қиылысу нүктесі х1 –ді берілген теңдеудің жуық түбірі деп қабылдаймыз және оның координаталарын анықтаймыз. Ол үшін (8) теңдеуге y=0 және x=x1 мәндерін қойып‚ х1 –ді есептеу формуласын табамыз.
Табылған шешімді жуық түбір деп аламыз. Ал егер х1 – түбір (3) –шартты қанағаттандырмаса‚ жоғарыдағы іс-әрекеттерді
Ізделіп жатқан түбір енді Осылайша итерацияны
формуласымен есептеуді‚ Сонымен трансцендент және алгебралық теңдеулерді хорда әдісімен шешу формуласы
Мысал:
Түбірді
формуламен есептейміз.
Есептеуді төртінші итерацияда тоқтатамыз. 2.5 Жанамалар әдісі.
Жанамалар әдісін кейде Ньютон әдісі деп те айтуға болады. Сонымен, 1-жағдай. а) б)
Осы өрнекте y=0,
Егер табылған түбір (3) шартты қанақаттандырмаса, келесі түбірді
Егер Жалпы алғанда
формуламен, 2-жағдай. а) б) Осы өрнектердің біреуін көріп шығайық.
Осы теңдеуге
өрнегін аламыз. Егер (3) шарт орындалмаса,
Жалпы алғанда, есептеуді
формуласымен, |



 санын алайық. Бұл сан иррационал болғандықтан оның мәні белгісіз(
санын алайық. Бұл сан иррационал болғандықтан оның мәні белгісіз(  a = A – a.
a = A – a. .
. = 0.0059…..
= 0.0059…..

 - салыстырмалы қателік болса, онда
- салыстырмалы қателік болса, онда  шектелген салыстырмалы
шектелген салыстырмалы 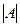
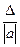 ,
, 
 5,373
5,373 
 +
+  + ... +
+ ... + 
 , болса, онда
, болса, онда  , болады.
, болады. - аргументтер xi – тің абсолютті қателіктері болсын. Сонда функцияның абсолютті қателігі
- аргументтер xi – тің абсолютті қателіктері болсын. Сонда функцияның абсолютті қателігі
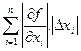
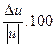 %.
%. (1)
(1) функциясы
функциясы  аралығында анықталған және үздіксіз.
аралығында анықталған және үздіксіз. =0 теңдігі орындалатын x саны осы теңдеудің түбірі немесе шешімі деп аталады.
=0 теңдігі орындалатын x саны осы теңдеудің түбірі немесе шешімі деп аталады. (2)
(2) – кез келген нақты сандар; n – натурал сандар.
– кез келген нақты сандар; n – натурал сандар. =14;
=14; .
.

 -тың таңбасы өзгермесе, онда
-тың таңбасы өзгермесе, онда  шарттарының бірінің орындалуы қажетті және жеткілікті.
шарттарының бірінің орындалуы қажетті және жеткілікті. (монотон өсуші) немесе
(монотон өсуші) немесе  (монотон кемуші) шарттары орындалса.
(монотон кемуші) шарттары орындалса.
 .
.


 және жуық түбірін
және жуық түбірін  деп белгілейік. Ал e – берілген өте кіші сан болсын.
деп белгілейік. Ал e – берілген өте кіші сан болсын. e шарты орындалса, онда
e шарты орындалса, онда  (3)
(3) аралығында бөлектенген болсын, яғни бұл аралықта
аралығында бөлектенген болсын, яғни бұл аралықта  шарт орындалады. d=b-а аралықтың ұзындығы. Теңдеудің түбірін e дәлдікпен табайық. Түбір
шарт орындалады. d=b-а аралықтың ұзындығы. Теңдеудің түбірін e дәлдікпен табайық. Түбір 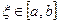 болғандықтан
болғандықтан 
 -ны түбірдің кемімен алынған жуық мәні, ал b-ны түбірдің артықымен алынған жуық мәні дейміз. Теңдеудің түбірі ретінде
-ны түбірдің кемімен алынған жуық мәні, ал b-ны түбірдің артықымен алынған жуық мәні дейміз. Теңдеудің түбірі ретінде  санын аламыз. Егер
санын аламыз. Егер  болса, теңдеудің түбірі ретінде а мен b-ны түбірдің артығымен алынған жуық мәні дейміз. Теңдеудің түбірі ретінде a-мен b-ның арасында жатған кез келген
болса, теңдеудің түбірі ретінде а мен b-ны түбірдің артығымен алынған жуық мәні дейміз. Теңдеудің түбірі ретінде a-мен b-ның арасында жатған кез келген  , болса
, болса  нүктені табайық. Онда берілген аралығымыз ұзындығы
нүктені табайық. Онда берілген аралығымыз ұзындығы  -ге тең болатын екі аралыққа бөлінеді. Осы екі аралықтың қайсысында
-ге тең болатын екі аралыққа бөлінеді. Осы екі аралықтың қайсысында 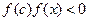 шарты орындалса‚ сол аралықты таңдап аламыз. Егер кесінді ұзындығы
шарты орындалса‚ сол аралықты таңдап аламыз. Егер кесінді ұзындығы  болса, онда түбір ретінде
болса, онда түбір ретінде  немесе
немесе  аламыз. Ал шарт орындалмаса жоғарыдағы іс-әрекеттерді қайталаймыз. Сонымен аралықты қақ бөлуді
аламыз. Ал шарт орындалмаса жоғарыдағы іс-әрекеттерді қайталаймыз. Сонымен аралықты қақ бөлуді  (n – бөлулер саны) шарт орындалғанша жалғастырамыз.
(n – бөлулер саны) шарт орындалғанша жалғастырамыз. теңдеуінің
теңдеуінің  аралықтағы түбірін
аралықтағы түбірін 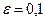 дәлдікпен табайық.
дәлдікпен табайық.

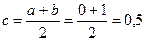

 аралығын таңдап аламыз.
аралығын таңдап аламыз. 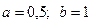

 аралығын қарастырамыз.
аралығын қарастырамыз. 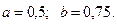


 Сонымен шарт орындалды. Түбір ретінде
Сонымен шарт орындалды. Түбір ретінде  аралығында жататын кез-келген
аралығында жататын кез-келген  -ның арифметикалық ортасын аламыз.
-ның арифметикалық ортасын аламыз.
 . Теңдеудің түбірін
. Теңдеудің түбірін  дәлдікпен табайық. Хордалар әдісін қолдануды екі жағдай үшін қарастырамыз.
дәлдікпен табайық. Хордалар әдісін қолдануды екі жағдай үшін қарастырамыз.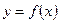 функциясының бірінші және екінші туындыларының таңбалары бірдей‚ яғни
функциясының бірінші және екінші туындыларының таңбалары бірдей‚ яғни  болсын. Онда:
болсын. Онда:
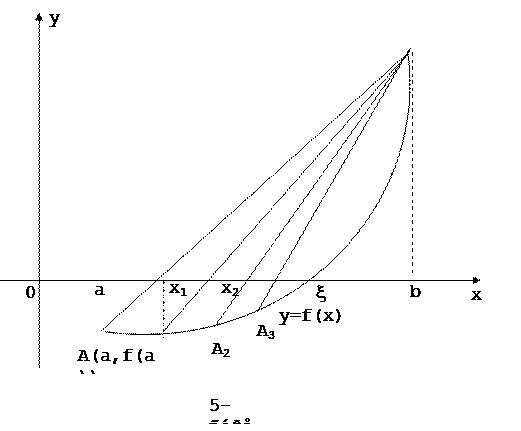
 (4)
(4) (5)
(5) аралығында іздейміз. Жоғарыдағы іс-әрекеттерді осы аралықта қайталап‚
аралығында іздейміз. Жоғарыдағы іс-әрекеттерді осы аралықта қайталап‚ 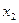 - түбірдің координатасын анықтаймыз.
- түбірдің координатасын анықтаймыз. (6)
(6) шарт орындалмаса‚ келесі
шарт орындалмаса‚ келесі 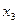 - түбірді есептейміз т.с.с.
- түбірді есептейміз т.с.с. (7)
(7) шарт орындалғанша жалғастырамыз. Осы көрсетілген формула (7)
шарт орындалғанша жалғастырамыз. Осы көрсетілген формула (7)  өрнектері үшін де орынды ( b - вариант).
өрнектері үшін де орынды ( b - вариант). .
.

 теңдеуінің бастапқы түбірі х0 – деп
теңдеуінің бастапқы түбірі х0 – деп  (8)
(8) (9)
(9) аралық үшін қайталап‚ х2-ті табамыз.
аралық үшін қайталап‚ х2-ті табамыз. (10)
(10) аралықта жатады. Егер табылған түбір
аралықта жатады. Егер табылған түбір  (11)
(11) өрнектері үшін де орынды.
өрнектері үшін де орынды. болса‚ онда (11) формуламен есептеледі.
болса‚ онда (11) формуламен есептеледі. теңдеуінің
теңдеуінің  аралықтағы түбірін
аралықтағы түбірін  дәлдікпен табайық.
дәлдікпен табайық.


 жоғарыдағы теңдеудің
жоғарыдағы теңдеудің  функциясы үздіксіз және
функциясы үздіксіз және  шарт орындалады. Теңдеудің түбірі
шарт орындалады. Теңдеудің түбірі  функциясының бірінші және екінші туындыларының таңбасы бірдей, яғни
функциясының бірінші және екінші туындыларының таңбасы бірдей, яғни  . Онда төмендегі өрнектер орынды:
. Онда төмендегі өрнектер орынды:

 Осылардың біреуін көріп шығайық.
Осылардың біреуін көріп шығайық.
 -аламыз. Графиктегі B нүктесінен жүргізілген жанама теңдеуін анықтаймыз
-аламыз. Графиктегі B нүктесінен жүргізілген жанама теңдеуін анықтаймыз (12)
(12) мәндерін қойып,
мәндерін қойып,  - ді табамыз.
- ді табамыз. (13)
(13) (14)
(14) шартты орындамаса, онда келесі
шартты орындамаса, онда келесі  (15)
(15) түбірді
түбірді  . Онда төмендегі шарттар орынды:
. Онда төмендегі шарттар орынды:



 (16)
(16) мәндерін қойып
мәндерін қойып (17)
(17) аралықтан
аралықтан  (19)
(19)