 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Системный анализ и синтез.
Для ответа на поставленные вопросы существуют специальные статистические методы и, соответственно, показатели, значения которых определенным образом (и с определенной вероятностью) свидетельствуют о наличии или отсутствии линейной связи между переменными. В первом случае это коэффициент корреляции величин x и y, во втором случае — коэффициенты линейной регрессии a и b, их стандартные ошибки и t-статистики, по значениям которых проверяется гипотеза об отсутствии связи величин x и y. В качестве меры для степени линейной связи двух переменных используется коэффициент их корреляции. Формула расчета выборочного коэффициента корреляции величин x и y, который рассчитывается по данным выборки, имеет вид
где
показателей;
независимой переменной;
зависимой переменной;
n — число значений переменных.
Если переменные независимы, то коэффициент корреляции близок нулю и наоборот. Далее для оценки тесноты связи этих переменных воспользуемся данными таблицы 3.
Таблица 3 — Оценка тесноты связи переменных
Чтобы определить уравнение линейной регрессии и его коэффициенты, используется метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции, который называется методом наименьших квадратов. Коэффициенты линейной регрессии у = ах + b определяются из системы уравнений
Коэффициенты а и b определяются по формуле
Уравнение функциональной зависимости можно найти, используя функции «НАКЛОН» и «ОТРЕЗОК» в прикладной программе Excel. Функция «НАКЛОН» позволяет определить значение a, т. е. наклон линии линейной регрессии. Функция «ОТРЕЗОК» позволяет определить значение свободного члена линейной регрессии b. Так как для генеральной совокупности выборочный коэффициент корреляции является случайной величиной, то для нее он может быть равен нулю. Для проверки гипотезы о равенстве коэффициента корреляции для генеральной совокупности нулю используют t-статистику (имеющая распределение Стьюдента (n-2) степенями свободы), рассчитываемая по формуле
где
n — число значений переменных.
Для проверки нулевой гипотезы находят по таблице Стьюдента (таблица 4) критическое значение tтабл при заданной доверительной вероятности Р = 0,95 или P = 0,99 и числе степеней свободы υ = n – 2. Далее необходимо сопоставить критическое значение tтабл с определенным по выборочным данным значение t-статистики. Если расчетная величина t-критерия окажется больше табличной, то это означает, что полученный коэффициент корреляции значимо отличается от нуля, если же расчетное значение критерия меньше, чем табличное, то коэффициент корреляции следует считать равным нулю. Таблица 4 — Критические значения критерия Стьюдента tk (Р, υ)
|



 (1)
(1) — коэффициент корреляции;
— коэффициент корреляции;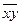 — среднее значение произведения величин используемых
— среднее значение произведения величин используемых — среднее значение показателя, рассматриваемого в качестве
— среднее значение показателя, рассматриваемого в качестве — среднее значение показателя, рассматриваемого в качестве
— среднее значение показателя, рассматриваемого в качестве — среднеквадратическое отклонение величины x;
— среднеквадратическое отклонение величины x; , (2)
, (2) — среднеквадратическое отклонение величины y.
— среднеквадратическое отклонение величины y. (3)
(3)
 (4)
(4)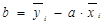 . (5)
. (5) (6)
(6) — расчетная величина критерия Стьюдента;
— расчетная величина критерия Стьюдента;