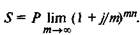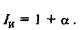ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ФИНАНСОВОГО МЕНЕДЖМЕНТА

ЛЕКЦИЯ № 2

БАЗОВЫЕ ПОНЯТИЯ ФИНАНСОВОГО МЕНЕДЖМЕНТА

БАЗОВЫЕ ПОКАЗАТЕЛИ

Четыре основных показателя, используемых уже не только в западной, но и в отечественной практике.

Первый: добавленная стоимость(ДС).

Если из стоимости продукции, произведенной, а не только реализованной предприятием за тот или иной период (включая увеличение запасов готовой продукции и незавершенное производство), вычесть стоимость потребленных материальных средств производства (сырья, энергии и пр.) и услуг других организаций, то получится стоимость, которую действительно добавили к стоимости сырья, энергии, услуг.Величина добавленной стоимости свидетельствует о масштабах деятельности предприятия и о его вкладе в создание национального богатства. Вычтем из ДС налог на добавленную стоимость и перейдем к конструированию следующего показателя.

Второй: брутто-результат эксплуатации инвестиций (БРЭИ).

Вычтем из ДС расходы по оплате труда и все связанные с ней обязательные платежи предприятия (по социальному страхованию, пенсионному обеспечению и проч.), а также все налоги иналоговые платежи предприятия, кроме налога на прибыль — получим БРЭИ.

БРЭИ используется в финансовом менеджменте как один из основных промежуточных результатов финансово-хозяйственной деятельности предприятия. Представляя собой прибыль до вычета амортизационных отчислений, финансовых издержек по заемным средствам и налога на прибыль, величина БРЭИ является первейшим показателем достаточности средств на покрытие всех этих расходов (налоги — те же расходы, не так ли?). Более того, по удельному весу БРЭИ в добавленной стоимости можно судить об эффективности управления предприятием и составить общее представление о потенциальной рентабельности и гибкости предприятия.

Третий: нетто-результат эксплуатации инвестиций (НРЭИ),или прибыль до уплаты процентов за кредит и налога на прибыль.

Из предыдущего показателя вычтем все затраты на восстановление основных средств — это и будет нетто-результат эксплуатации инвестиций. По существу, этот экономический эффект, снимаемый предприятием с затрат, представляет собой прибыль до уплаты процентов за кредиты и займы и налога на прибыль. Поэтому на практике для быстроты расчетов можно принимать за НРЭИ балансовую прибыль (БП), восстановленную до нетто-результата эксплуатации инвестиций прибавлением процентов за кредиты, относимых на себестоимость продукции (работ, услуг). Таким способом можно избежать двойного счета процентов, ибо часть их, относимая, по действующему законодательству, на чистую прибыль, остающуюся в распоряжении предприятия, содержится в самой балансовой прибыли.

Четвертый: экономическая рентабельность (ЭР) активов,или, что то же, экономическая рентабельность всего капитала предприятия,т. е. суммы его собственных и заемных средств.

Мы будем пользоваться показателем, основанным на наиболее общей формуле рентабельности производства, характеризующей эффективность затрат и вложений:

Что подставить в числитель этой формулы, вы, конечно, уже поняли — НРЭИ. А в знаменатель, помня, что именно в активе баланса предприятия отражены направления расходования и вложений средств, подставим объем актива:

Поскольку актив и пассив равны, а последний представляет собой совокупность собственных средств и заимствований,

ЭР — жизненно важный показатель для предприятия, ведь достаточный уровень экономической рентабельности — свидетельство нынешних и залог будущих успехов.

Преобразуем формулу экономической рентабельности, умножив ее на ОБОРОТ/ОБОРОТ = 1. От такой операции величина рентабельности не изменится, зато проявятся два важнейших элемента рентабельности: коммерческая маржа (КМ)и коэффициент трансформации (КТ).

Коммерческая маржа показывает, какой результат эксплуатации дают каждые 100 руб. оборота (обычно КМ выражают в процентах). По существу, это экономическая рентабельность оборота, или рентабельность продаж, рентабельность реализованной продукции. У предприятий с высоким уровнем прибыли КМ превышает 20 и даже 30%, у других едва достигает 3 — 5%.

КТ показывает, сколько рублей оборота снимается с каждого рубля актива, т. е. в какой оборот трансформируется каждый рубль актива. КТ можно также воспринимать как оборачиваемость активов. В такой трактовке КТ показывает, сколько раз за данный период оборачивается каждый рубль активов.

Часто используемый в практической работе вариант: берем показатель чистой рентабельности (прибыльности) активов (ПРИБЫЛЬ ПОСЛЕ УПЛАТЫ НАЛОГА/АКТИВ) и умножаем на ОБОРОТ/ОБОРОТ = 1. Получаем: ЧИСТАЯ РЕНТАБЕЛЬНОСТЬ АКТИВОВ = ЧИСТАЯ РЕНТАБЕЛЬНОСТЬ (ПРИБЫЛЬНОСТЬ) ОБОРОТА х ЧИСТАЯ ОБОРАЧИВАЕМОСТЬ АКТИВОВ. Таким образом, мы вновь приходим к знаменитой формуле Дюпона. Эта формула позволяет определить, какие факторы в наибольшей степени повлияли на чистую рентабельность активов.

У формулы Дюпона есть и весьма полезная модификация, вводящая в анализ показатель чистой рентабельности (прибыльности, доходности) акционерного капитала. Это частное от деления чистого дохода (чистой прибыли) по обыкновенным акциям на сумму акционерного капитала:

При сильном возрастании чистой рентабельности акционерного капитала по этой формуле можно определить, за счет чего это произошло: благодаря увеличению чистой прибыли на каждый рубль оборота? за счет более эффективного использования активов? за счет изменения или более рационального использования акционерного капитала? за счет сопряженного воздействия этих факторов? и т. д.

Регулирование экономической рентабельности сводится к воздействию на обе ее составляющие: и коммерческую маржу, и коэффициент трансформации:«При низкой прибыльности продаж необходимо стремиться к ускорению оборота капитала и его элементов и, наоборот, определяемая теми или иными причинами низкая деловая активность предприятия может быть компенсирована только снижением затрат на производство продукции или ростом цен на продукцию, т. е. повышением рентабельности продаж».

На КМ влияют такие факторы, как ценовая политика, объем и структура затрат и т. п. КТ складывается под воздействием отраслевых условий деятельности, а также экономической стратегии самого предприятия. Примирить высокую коммерческую маржу с высоким коэффициентом трансформации очень трудно, ибо оборот присутствует в числителе одного сомножителя и в знаменателе другого. Поэтому при наращивании оборота удается увеличить экономическую рентабельность только тогда, когда под возросший оборот подставляют «нераздутые» активы, и НРЭИ начинает расти быстрее оборота. В анализе факторов изменения рентабельности главное — решить вопрос, какой из показателей: коммерческая маржа или коэффициент трансформации изменяется сильнее и быстрее, оказывая тем самым более мощное воздействие на общий уровень экономической рентабельности активов.

Для предприятия всегда важно выбрать отрасль, сферу деятельности. Действительно, различия в фондоемкости и ценовые факторы могут оказать решающее влияние на уровень экономической рентабельности. Но, независимо от отраслевой принадлежности, предприятия располагают все-таки определенной свободой маневра, чтобы усилить КМ (воздействуя на себестоимость, снижая расходы по реализации продукции, упорядочивая административно-управленческие расходы) и улучшить КТ. Второе требует, впрочем, более тонких инструментов. Часто проводят аналогию с человеческим организмом: для жизнедеятельности нужны и кости, и мышцы; немалую роль играет наследственность. Но одни люди держат форму, другие — нет. Хорошо бы найти и сохранять такой вес, при снижении которого человек слабеет, а при повышении — становится грузным и неповоротливым. Для поддержания такого веса нужно избавиться от излишков жира и потреблять лишь жизненно необходимые вещества. То же самое — и для актива предприятия. Надо «поглощать» машины, запасы, товарную задолженность, чтобы не погибнуть от истощения, но это не значит, что можно питаться чем и как попало. И актив должен вести здоровый образ жизни! Каждый лишний рубль актива может стать тормозом для развития предприятия:

• чем больше средств задействовано для достижения заданной величины оборота, тем больше усилий будет затрачено на их конверсию в случае переориентации деятельности предприятия;

• если предприятие обращается к новым видам и сферам деятельности, руководствуясь лишь максимизацией коммерческой маржи и недооценивая коэффициент трансформации, последствия грозят быть плачевными.

Четырех базовых показателей финансового менеджмента и формулы Дюпона достаточно, чтобы приступить к рассмотрению жизнедеятельности предприятия. Но необходимо учесть некоторые нюансы.

1. Анализ обычно проводится за какой-то период по отчетности, составленной на определенную дату. Но на протяжении этого периода объем баланса и отдельные его статьи претерпевают колебания, иногда весьма значительные. Поэтому серьезный финансист не поленится рассчитать соответствующие среднеарифметические, а еще лучше — среднехронологические величины. Это непременное условие получения реалистичных результатов анализа, пригодных для принятия разумных финансовых решений, может быть отнесено ко всем расчетам в финансовом менеджменте.

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ФИНАНСОВОГО МЕНЕДЖМЕНТА

Четкое представление о базовых понятиях финансовой математики необходимо для понимания всего последующего материала.

Проценты— это доход от предоставления капитала в долг вразличных формах (ссуды, кредиты и т. д.), либо от инвестиций производственного или финансового характера.

Процентная ставка— это величина, характеризующая интенсивность начисления процентов.

Величина получаемого дохода (т. е. процентов) определяется исходя из величины вкладываемого капитала, срока, на который он предоставляется в долг или инвестируется, размера и вида процентной ставки (ставки доходности).

Наращение (рост) первоначальной суммы долга— это увеличение суммы долга за счет присоединения начисленных процентов (дохода).

Множитель (коэффициент) наращения— это величина, показывающая, во сколько раз вырос первоначальный капитал.

Период начисления— это промежуток времени, за который начисляются проценты (получается доход). В дальнейшем будем полагать, что период начисления совпадает со сроком, на который предоставляются деньги. Период начисления может разбиваться на интервалы начисления.

Интервал начисления— это минимальный период, по прошествии которого происходит начисление процентов.

Существуют две концепции и, соответственно, два способа определения и начисления процентов.

Декурсивный способ начисления процентов. Проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из величины предоставляемого капитала. Соответственно декурсивная процентная ставка, или, что то же, ссудный процент, представляет собой выраженное в процентах отношение суммы начисленного за определенный интервал дохода к сумме, имеющейся на начало данного интервала.

Антисипативный способ (предварительный) начисления процентов. Проценты начисляются в начале каждого интервала начисления. Сумма процентных денег определяется исходя из наращенной суммы. Процентной ставкой будет выраженное в процентах отношение суммы дохода, выплачиваемого за определенный интервал, к величине наращенной суммы, полученной по прошествии этого интервала. Определяемая таким способом процентная ставка называется (в широком смысле слова) учетной ставкой или антисипативным процентом.

В мировой практике декурсивный способ начисления процентов получил наибольшее распространение. В странах развитой рыночной экономики антисипативный метод начисления процентов применялся, как правило, в периоды высокой инфляции.

При обоих способах начисления процентов процентные ставки могут быть либо простыми(если они применяются к одной и той же первоначальной денежной сумме в течение всего периода начисления), либо сложными(если по прошествии каждого интервала начисления они применяются к сумме долга и начисленных за предыдущие интервалы процентов).

2.1. Простые ставки ссудных процентов

Простые ставки ссудных (декурсивных) процентов применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (и составляет, как правило, срок менее одного года), или когда после каждого интервала начисления кредитору выплачиваются проценты. Естественно, простые ставки ссудных процентов могут применяться и в любых других случаях по договоренности участвующих в операции сторон.

Введем следующие обозначения:

i{%) — простая годовая ставка ссудного процента;

i — относительная величина годовой ставки процентов;

I_г — сумма процентных денег, выплачиваемых за год;

I — общая сумма процентных денег за весь период начисления;

Р — величина первоначальной денежной суммы;

S — наращенная сумма;

к_н — коэффициент наращения;

п — продолжительность периода начисления в годах;

д — продолжительность периода начисления в днях;

К — продолжительность года в днях.

Величина К является временной базойдля расчета процентов.

В зависимости от способа определения продолжительности финансовой оперции рассчитывается либо точный, либо обыкновенный (коммерческий) процент.

Дата выдачи и дата погашения ссуды всегда считаются за один день. При этом возможны два варианта:

вариант I. используется точное число дней ссуды, определяемое по специальной таблице, где показаны порядковые номера каждого дня года; из номера, соответствующего дню окончания займа, вычитают номер первого дня;

вариант 2 берется приблизительное число дней ссуды, когда продолжительность полного месяца принимается равной 30 дням; этот метод используется, когда не требуется большая точность, например, при частичном погашении займа.

Точный процент получают, когда за временную базу берут фактическое число дней в году (365 или 366) и точное число дней ссуды.

Приведенным вышеопределениям соответствуют формулы:

Применяя последовательно формулы (1.4), (1.3), (1.2) и (1.6), получаем основную формулу для определения наращенной суммы :

На практике часто возникает обратная задача: узнать величину суммы Р которая в будущем должна составить заданную величину S. В этом случае Р называется современной (текущей, настоящей , приведенной) величиной суммы S.

Определение современной величины Р наращенной суммы S называется дисконтированием,а определение величины наращенной суммы S — компаундингом.

В применении к ставке ссудного процента может также встретиться название математическое дисконтирование,несовместимое, кстати говоря, с учетными ставками, которые будут рассматриваться в следующем разделе.

Из формулы получаем формулу, соответствующую операции дисконтирования:

Преобразуя формулу (т. е. заменяя входящие в нее выражения на эквивалентные и выражая одни величины через другие), получаем еще несколько формул для определения неизвестных величин в различныхслучаях:

Иногда на разных интервалах начисления применяются разные процентные ставки.

При N интервалах начисления наращенная суммасоставит

Для множителя наращения, следовательно, имеем

2.2. Простые учетные ставки

При антисипативном способе начисления процентов сумма получаемого дохода рассчитыва_ется исходя из суммы, получаемой по прошествии интервала Начисления (т. е. из наращенной суммы). Эта сумма и считается величиной получаемого кредита (или ссуды). Так как в данном случае проценты начисляются в начале каждого интервала начисления, заемщик, естественно, получает эту сумму за вычетом процентных денег. Такая операция называется дисконтированием _по учетной ставке,а также коммерческимили банковским учетом

Дисконт— это доход, полученный по учетной ставке, т. е. разница между размером кредита и непосредственно выдаваемой суммой.

Пусть теперь

d(%) — простая годовая учетная ставка;

d — относительная величина учетной ставки;

D_a — сумма процентных денег выплачиваемая за год;

D — общая сумма процентных денег

S - сумма, которая должна быть возвращена;

Р — сумма, получаемая заемщиком.

Тогда, согласно определениям, имеем следующие формулы:

Преобразуя последнее выражение, получаем формулу для определения наращенной суммы:

На практике учетные ставки применяются главным образом при учете (т. е. покупке) векселей и других денежных обязательств.

Из приведенных формул можно вывести еще две формулы для определения периода начисления и учетной ставки при прочих заданных условиях:

2.3. Сложные ставки ссудных процентов

Если после очередного интервала начисления доход (т. е. начисленные за данный интервал проценты) не выплачивается, а присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют формулы сложных процентов. Сложные ссудные проценты в настоящее время являются весьма распространенным видом применяемых в различных финансовых операциях процентных ставок.

Пусть

i_с — относительная величина годовой ставки сложных ссудных процентов;

к_н _с — коэффициент наращения в случае сложных процентов;

j — номинальная ставка сложных ссудных процентов (ее определение будет дано в дальнейшем).

Если за интервал начисления принимается год, то по прошествии первого года наращенная сумма, в соответствии с формулой (1.7), составит

Еще через год этовыражение применяется уже к сумме S₁.

и так далее. Очевидно, что по прошествии п лет наращенная сумма составит

Множитель наращения к_н _с соответственно будет равен

При начислении простых процентов он составил бы по формулам:

Когда возникает возможность выбора между низкой сложной процентной ставкой и более высокой простой, следует отдавать предпочтение первому варианту. Естественно, если в нашем распоряжении более или менее значительный период времени. Сумма, наращенная по сложной процентной ставке, уже через небольшое (в зависимости от разницы в величине процентных ставок) количество интервалов начисления превысит сумму, наращенную по простой ставке (см. рис. 1). Подробно этот вопрос рассматривается в разделе 2.5.

Если срок ссуды п в годах не является целым числом, множитель наращения определяют по выражению:

где п = п_а + п_ь;

п_а — целое число лет;

п_ь — оставшаяся дробная часть года.

В мировой практике часто применяется также непрерывное начисление сложных процентов (т. е. продолжительность интервала начисления стремится к нулю, а т — к бесконечности).

В этом случае для вычисления наращенной суммы служит следующее выражение:

Для расчетов можно использовать известную в математике формулу 1 зам предела:

где е = 2,71828...

Из этой формулы следует:

Тогда для наращенной суммы получаем:

S=Pe^jn

2.4. Сложные учетные ставки

Рассмотрим теперь антисипативный способ начисления сложных процентов.

Пусть

d_c (%) — сложная годовая учетная ставка;

d_c — относительная величина сложной учетной ставки;

к^у — коэффициент наращения для случая учетной ставки;

/ — номинальная годовая учетная ставка.

Тогда по прошествии первого года наращенная сумма S\ в соответствии с формулой составит

Еще через год эта формула будет применяться уже к сумме S1.

и т. д., аналогично случаю сложных ставок ссудных процентов. По прошествии и лет наращенная сумма составит

Отсюда для множителя наращения имеем

Утверждение, что декурсивный метод начисления более выгоден для заемщика, а антисипативный — для кредитора. Это можно считать справедливым лишь для небольших процентных ставок, когда расхождение не столь значительно. Но с ростом процентной ставки разница в величине наращенной суммы становится огромной (при этом она сама растет с ростом л), и сравнение двух методов с точки зрения выгодности утрачивает смысл.

2.5. Эквивалентность процентных ставок различного типа

Часто при расчетах, проводимых по различным финансовым операциям, возникает необходимость в определении эквивалентных процентных ставок.

Эквивалентные процентные ставки— это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.

Эквивалентные процентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок.

Для нахождения эквивалентных процентных ставок используют уравнения эквивалентности,принцип составления которых заключается в следующем. Выбирается величина, которую можно рассчитать при использовании различных процентных ставок. На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида.

Для различных случаев сложных процентов получаем уравнение эквивалентности:

Полученная годовая ставка сложных процентов (i_c), эквивалентная номинальной процентной ставке, называется эффективной ставкойсложных процентов.

Эффективную ставку сложных процентов полезно знать, чтобы оценить реальную доходность финансовой операции, или сравнить процентные ставки в случае, когда используются различные интервалы начисления. Очевидно, что значение эффективной процентной ставки больше значения номинальной, а совпадают они при т = 1.

Далее имеем

Аналогичным образом получаем зависимости между любымидругими эквивалентными процентными ставками.

2.6. Учет инфляционного обесценения денег в принятии финансовых решений

Инфляция характеризуется обесценением национальной валюты (т. е. снижением ее покупательной способности) и общим повышением цен в стране. Очевидно, что в различных случаях влияние инфляционного процесса сказывается неодинаково. Так, если кредитор (инвестор) теряет часть дохода за счет обесценения денежных средств, то заемщик может получить возможность погасить задолженность деньгами сниженной покупательной способности.

Во избежание ошибок и потерь в условиях снижения покупательной способности денег рассмотрим механизм влияния инфляции на результат финансовых операций и проведем несложные математические расчеты и преобразования.

Пусть S_a — сумма, покупательная способность которой с учетом инфляции равна покупательной способности суммы при отсутствии инфляции. Через AS обозначим разницу между этими суммами.

Отношение ΔS /S, выраженное в процентах, называется уровнем инфляции.

При расчетах используют относительную величину уровня инфляции — темп инфляции а.

Тогда дляопределения S_a получаем следующее выражение:

Величину (1 + а), показывающую, во сколько раз S_a больше S (т. е. во сколько раз в среднем выросли цены), называют индексом инфляцииI_н.

Динамика индекса инфляции за несколько лет отражает изменения, происходящие в инфляционных процессах. Понятно, что повышение индекса инфляции за определенный период по сравнению с предыдущим таким же периодом указывает на ускорение инфляции, снижение — на уменьшение ее темпов.

Формула И. Фишера

i_a – ставка ссудного процента учитывающего инфляцию

a – темп инфляции

i – относительная величина годовой ставки процентов

a+ia-инфляционной премией.