ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Алгоритм k ближайших соседей

Применение нейронных сетей

Возникает следующий важный вопрос: как применить нейронную сеть к решению конкретной задачи? Класс задач, которые можно решить с помощью нейронной сети, определяется тем, как сеть работает и как она обучается.

Таким образом, сеть можно применять в ситуации, когда имеется определенная известная информация, и вы хотите из нее получить некоторую пока неизвестную информацию (Patterson, 1996; Fausett, 1994).

Распознавание состояния больного

Применение классических статистических методов для решения этой задачи описано еще в работах Неймана. С помощью медицинской аппаратуры можно наблюдать за различными показателями состояния здоровья человека (например, частотой пульса, содержанием различных веществ в крови, частотой дыхания). Стадии возникновения некоторой болезни может соответствовать определенная и весьма сложная (например, нелинейная и взаимозависимая) комбинация изменений наблюдаемых переменных, которая может быть обнаружена с помощью нейросетевой модели.

Прогнозирование на фондовом рынке

Колебания цен на акции и фондовых индексов - еще один пример сложного, многомерного, но в определенных ситуациях частично прогнозируемого явления. Многие финансовые аналитики используют нейронные сети для прогнозирования цен акций на основе многочисленных факторов, например, прошлого поведения цен этих и других акций в совокупности с различными другими экономическими показателями. В качестве альтернативных вариантов здесь применяются модели авторегрессии и технический анализ.

Предоставление кредита

Как правило, у банка имеется большой набор сведений о человеке, обратившемся с просьбой о предоставлении кредита. Это может быть его возраст, образование, род занятий и многие другие данные. Обучив нейронную сеть на уже имеющихся данных, аналитик определяет наиболее существенные характеристики и на их основе относит данного клиента к категории с высоким или низким кредитным риском. Заметим, что для решения подобных задач можно параллельно использовать и классические статистические методы, такие как дискриминантный анализ и деревья классификации.

Системы слежения за состоянием оборудования

Нейронные сети оказались полезны как средство контроля состояния производственного процесса и состояния оборудования. Нейронная сеть может быть обучена так, чтобы отличать шум, который издает машина при нормальной работе («ложная тревога») от того, который является предвестником неполадок. После такого обучения нейронная сеть может предупреждать инженеров об угрозе поломки до того, как она случится, и тем самым исключать неожиданные и дорогостоящие простои.

Управление работой двигателя

Нейронные сети используются для анализа сигналов от датчиков, установленных на двигателях. С помощью нейронной сети можно управлять различными параметрами работы двигателя, чтобы достичь определенной цели, например, уменьшить потребление горючего.

Важное условие применения нейронных сетей: вы должны знать (или хотя бы иметь серьезные подозрения), что между известными входными значениями и неизвестными выходами имеется связь. Эта связь может быть искажена шумом, но она должна существовать (так, едва ли можно ожидать, что по данным из примера с прогнозированием цен акций можно построить абсолютно точный прогноз, поскольку на цену влияют и другие факторы, не представленные во входном наборе данных, и кроме того, в задаче присутствует элемент случайности).

Как правило, нейронная сеть используется тогда, когда неизвестен точный вид связей между входами и выходами, - если бы он был известен, то связь можно было бы моделировать непосредственно. Другая существенная особенность нейронных сетей состоит в том, что зависимость между входом и выходом находится в процессе обучения сети. Для обучения нейронных сетей применяются алгоритмы двух типов (разные типы сетей используют разные типы обучения): управляемое («обучение с учителем») и неуправляемое («без учителя»). Чаще всего применяется обучение с учителем.

Модель нейронных сетей

Ключевым является понятие нейрона - специальной нервной клетки, способной воспринимать, преобразовывать и распространять сигналы.

Общая модель нейрона состоит в следующем: нейрон (neuron) имеет несколько каналов ввода информации - дендриты и канал вывода информации - аксон.

Аксон нейрона соединен с дендритами других нейронов с помощью синапсов (synapse). При возбуждении нейрон посылает сигнал по своему аксону.

Через синапсы сигнал передается другим нейронам, которые, в свою очередь, могут возбуждаться или, наоборот, переходить в состояние торможения.

Нейрон возбуждается, если суммарный уровень сигналов, пришедших в него, превышает некоторый уровень - порог возбуждения или активации (см. порог b в модели нейрона). Интенсивность сигнала, получаемого нейроном, зависит от активности синапсов.

Графически модель нейрона можно представить в виде, показанном на рис. 1. Из него видно, что на вход нейрона поступают сигналы х, каждый из которых умножается на вес w (для каждого сигнала имеется собственный вес); производится сложение преобразованных сигналов и добавляется порог (см.блок сумматор на диаграмме); результат преобразуется с помощью функции активации f и подается на выход нейрона.

Рис.1. Модель нейрона Ml

В модели Ml вес (weight) моделирует силу синапса.

Итак, запомним следующее:

- нейрон получает сигналы через несколько входных каналов, они показаны на схеме слева;

- каждый сигнал проходит через соединение - синапс, имеющее определенную силу или вес w(i,j), который соответствует синаптической активности нейрона;

- коэффициенты w(i,j) называются весами синаптических связей, положительное значения которых соответствуют возбуждающим синапсам, отрицательные значения - тормозящим синапсам; если w(i,j) = 0, то говорят, что связь между нейроном i и нейроном j отсутствует;

- текущее состояние нейрона описывается формулой:

(1)

где x(j), j = 1,2, …, N- входные сигналы;

- величина b(i) называется пороговым значением (порогом активации);

- полученный нейроном сигнал преобразуется с помощью нелинейной функции активации или передаточной функции/в выходной сигнал

y_i=f(u_i) (2)

Индекс i относится к номеру рассматриваемого нейрона в сети, индекс j указывает номер синаптической связи.

Данную модель нейрона называется моделью Ml. Это одна из первых моделей нейрона, предложенная МакКаллоком и Питсом в 1943 г.

Иногда формулу (1) записывают в следующем виде, добавляя нулевой синапс с единичным сигналом:

(3)

В этой модели для нулевого веса по определению полагаем w(i,0)=b(i), иными словами, вес нулевого синапса в модели (3) равен порогу модели (2).

Данная модель нейрона называется моделью М2. Ее графическое представление показано на рис. 2.

Рис. 2. Модель нейрона М2

Сравнивая рис.1 с рис.2, можно увидеть, что основное отличие модели Ml от модели М2 состоит в добавлении входного сигнала с весом, равным порогу. Очевидно, модели Ml и М2 эквивалентны. Мы чаще будем работать с моделью Ml, в которой в явном виде указан порог возбуждения b(i).

Рассматриваемые модели являются детерминистскими, - в них отсутствует случайность.

В вероятностной модели нейрона выходной сигнал является случайной величиной, принимающей значение +1, которое соответствует возбуждению, и значение -1, которое соответствует торможению с определенной вероятностью, зависящей от величины и.

Вероятность активации нейрона описывается логистической функцией

где Т - параметр, описывающий уровень шума.

Графическое представление вероятностной модели нейрона показано на рис.3.

Рис.3. Вероятностная модель нейрона

Основное отличие вероятностной модели от детерминистской состоит в том, что с вероятностью Р(у) на выходе наблюдается значение + 1, с вероятностью 1 - Р(у) значение -1.

Заметим, при параметре Т, стремящемся к 0, вероятностная модель переходит в детерминистскую.

Вероятностные модели нейронов используют в вероятностных нейронных сетях STATISTICA.

Функция активации или передаточная функция f - это некоторая нелинейная функция, моделирующая процесс передачи возбуждения.

Используются следующие основные типы функции активации.

1. Пороговая функция (threshold function) или функция единичного скачка, определяемая равенствами:

f(u) = 1, если и > 0, f(u) = 0, если и< 1. (4)

2. Сигмоидальная функция (sigmoid function) функция f вида

F(u)=1/(1+exp(-bu)), где b>0 (5)

3. Кусочно-линейная функция (pice-wise-function):

f(u)= 1, еслиu>0,5, f(u) = |u|, если |u|< 0,5, f(и) = 0, еслиu< 0,5.

4. Функция знак {сигнум):

f(u)= -1, если и< 0, f(u)= 1, если и > 0.

Объединенные между собой нейроны образуют сеть, моделирующую работу мозга. Эта модель способна получать информацию извне и обладает свойством самообучения.

С математической точки зрения модель нейрона строит нелинейное преобразование входного сигнала x(1), х(2),..., x(N) в выходной сигнал у.

Теоретически доказано, что с помощью таких простейших преобразований можно приближать очень сложные многомерные функции, следовательно, оценивать сложные зависимости (знаменитая теорема Колмогорова является основанием нейронных сетей).

Итак, каждый нейрон, как элемент сети, описывается своим набором весов и пороговых значений, а также функцией активации f.

Входной слой нейронов служит для ввода значений входных переменных, выходной слой - для вывода результатов. Последовательность слоев нейронов и их соединений называется архитектурой сети.

Задать есть - это значит задать ее архитектуру и параметры нейронов.

При работе сети на входные элементы подаются значения входных данных (входной сигнал), затем возбуждаются нейроны первого промежуточного слоя, второго промежуточного слоя и т.д.; в итоге преобразованный сигнал поступает на выходной слой.

Преобразование сигнала нейроном сети проводится следующим естественным образом:

- берется взвешенная сумма выходов элементов предыдущего слоя и вычитается пороговое значение;

- полученные значения преобразуются с помощью передаточной функции;

- в результате получается выходной сигнал нейрона, который поступает на вход следующего нейрона или подается на выход сети, если нейрон является конечным.

Принципиальным моментом является обучение сети.

Обучение сети - это подгонка свободных параметров с целью адаптации к внешним воздействиям.

Процесс обучения может проводиться различными способами. Различают обучение с учителем {supervised learning), контролирующим процесс обучения с помощью примеров с известными решениями, и обучение без учителя {unsupervised).

Рассмотрим обучение с учителем. Этот процесс можно представить себе следующим образом.

На вход обучаемой системы поступает сигнал из внешней среды. Копия этого сигнала поступает на вход учителя, который формирует правильный отклик (правильный ответ). Отклик учителя сравнивается с выходным сигналом ученика.

Разность между правильным решением и откликом сети представляет собой ошибку, которую следует уменьшить с помощью настройки свободных параметров. Для этого строится сумма квадратов ошибок, которая представляет собой функцию свободных параметров сети. Процесс обучения состоит в нахождении минимума этой функции.

Рис. Процесс обучения нейронной сети

Следует отметить, что обучение имеет крайность - переобучение, которого следует избегать (ученик «натаскивается» на решение однотипных задач).

Обучение без учителя проводится на основе принципа самоорганизации (selforganized) сети. Этот принцип реализован, например, в картах Кохонена.

Опишем модель Розенблатта, в которой нейрон обучается правилу классификации на основе принципа коррекции ошибок.

Персептрон Розенблатта

Обратимся вновь к описанной выше модели нейрона Ml.

Поставим вопрос: «Чему и как эту модель можно обучить?» Ответ дает замечательная по простоте и ясности конструкция Розенблатта.

Рассмотрим классификацию с учителем.

Пусть на вход нейрона поступает сигнал, который может принадлежать либо классу А, либо классу В. Спрашивается: можно научить нейрон различать эти классы?

Идея алгоритма обучения проста: представьте, вы имеете сигнал +1 (плюс 1) из класса А и сигналы -1 (минус 1) из класса В. Сигнал +1 может обозначать, например, напряжение, сигнал -1 - расслабление.

Имеется обучающая выборка с известными результатами классификации, которая позволяет контролировать процесс обучения.

Вначале рассмотрим случай одномерных сигналов.

В простейшем случае у нейрона имеется один вход и порог, следовательно, имеется два свободных параметра: вес w и порог активации b. В качестве функции активации в персептроне Розенблатта используется стандартная функция сигнум (знак).

Алгоритм начинает работу с нулевых значений параметров.

- Пусть на шаге п поступает очередной сигнал из обучающей выборки.

- На шаге п вычисляется состояние нейрона w(n)x(n) + b(n).

- Пусть w(n)x(n)+b(n) > 0, но объект отнесен к отрицательному классу В. Производится корректировка параметров по правилу: w(n+1)=w(n)-x(n), b(n+1)=b(n)-x(n).

• Пусть w(n)x(n)+b(n)<0, но объект отнесен к классу А, производится

корректировка параметров по правилу: w(n +1)=w(n)+x(n), b(n+1)=b(n)+x(n).

• В случае правильной классификации коррекция свободных параметров не производится.

Легко увидеть, что описанный алгоритм сойдется за несколько шагов.

Алгоритм обучения распространяется на двумерные сигналы. В этом случае в модели нейрона с двумя входами имеется три свободных параметра: веса w₁, w₂ и порог активации b.

Так как состояние нейрона с двумя входами и порогом b описывается линейной функцией w₁x₁+w₂x₂+b, то можно правильно классифицировать лишь множества, разделенные прямой линией (лежащие по разные стороны от прямой линии). Такие множества называются линейно разделимыми (рис. 4).

Если между двумя множествами нельзя провести прямую линию, отделяющую множества друг от друга, то очевидно, классификация с помощью персептрона невозможна (рис. 5).

В случае трех входных сигналов необходима плоскость, разделяющая два множества в пространстве, и т.д.

Естественное обобщение персептрона Розенблатта приводит к понятию многослойного персептрона.

Многослойный персептрон имеет входной слой, выходной слой и несколько слоев скрытых нейронов (hidden neuron), расположенных между входным и выходным слоем.

Распространение сигнала производится слева направо - от входного слоя к выходному через несколько нейронов скрытых слоев.

Заметим, ключевую роль в обучении многослойного персептрона играют нейроны скрытых слоев.

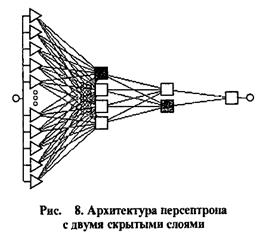
Многослойный персептрон имеет следующие особенности: гладкие функции активации (в отличие от скачкообразного сигнума, используемого в модели Розенблатта) и высокую степень связности (connectivity) нейронов, состоящую в том, что каждый нейрон скрытого слоя связан с нейронами предыдущего слоя.

Примеры многослойных персептронов показаны ниже на рис. 6-8.

Обучение многослойного персептрона производится с помощью алгоритма обратного распространения, точнее, алгоритма обратного распространения ошибки, являющегося модификацией градиентного спуска.

Термин «обратное распространение» связан с тем, что вектор ошибки распространяется по сети в сторону, обратную распространению входного сигнала.

В задачах классификации с гауссовскими исходными данными многослойные персептроны дают результаты, близкие к оптимальным байесовским.

Это связано с тем, что минимизация ошибок в задачах классификации в многослойном персептроне основана на функциях, аналогичных линейным дискриминантным функциям Фишера.

Алгоритм k ближайших соседей

Рассмотрим обучение, основанное на принципе памяти. Этот способ обучения используется в сетях радиальных базисных функций.

Простой эффективный алгоритм обучения на основе памяти - известный алгоритм k ближайших соседей.

В случае k = 1 алгоритм называется алгоритмом ближайшего соседа.

Идея алгоритма к ближайших соседей состоит в следующем:

- имеется достаточно большой набор входных сигналов с результатами правильной классификации;

- поступает новый сигнал х, который требуется классифицировать;

- в некоторой метрике измеряется расстояние до сигналов, представленных в исходном наборе, т.е. в памяти нейронной сети;

- строится сфера минимального радиуса с центром х, в которую попадают ровно k сигналов из памяти;

- новый сигнал относится к классу, представители которого с наибольшей частотой попали в данную сферу;

- в случае k = 1 в сферу попадает один элемент; этот элемент является ближайшим соседом для х; сигнал х относится к классу, которому принадлежит ближайший сосед.

С помощью компьютерного моделирования показано, что вероятность ложной классификации алгоритма ближайшего соседа в 2 раза выше вероятности ложной классификации оптимального байесовского классификатора. Важно отмстить, что алгоритм классификации методом ближайших соседей способен классифицировать множества, не являющиеся линейно разделимыми.

Ключевым моментом анализа является разделение исходных данных на обучающую, контрольную и тестовую выборку.

На обучающей выборке проводится обучение сети – оценка параметров сети. Естественно большая часть данных участвует в обучении сети.

Контрольная выборка контролирует процесс обучения, на тестовой выборке проводится оценка точности результатов (кромм-проверка).