 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Последовательность этапов регрессионного анализа 12
Основы анализа данных.
Типичной задачей, возникающей на практике, является определение зависимостей или связей между переменными. В реальной жизни переменные связаны друг с другом. Например, в маркетинге количество денег, вложенных в рекламу, влияет на объемы продаж; в медицинских исследованиях доза лекарственного препарата влияет на эффект; в текстильном производстве качество окрашивания ткани зависит от температуры, влажности и др. параметров; в металлургии качество стали зависит от специальных добавок и т.д. Найти зависимости в данных и использовать их в своих целях - задача анализа данных. Предположим, вы наблюдаете значения пары переменных X и Y и хотите найти зависимость между ними. Например: • X - количество посетителей интернет магазина, Y - объем продаж; • X - диагональ плазменной панели, Y - цена; • X - цена покупки акции, Y- цена продажи; • X - стоимость алюминия на Лондонской бирже, Y – объемы продаж; • X - количеством прорывов на нефтепроводах, Y - величина потерь; • X - «возраст» самолета, Y - расходы на его ремонт; • X - торговая площадь, Y - оборот магазина; • X - доход, Y - потребление и т. д.
Переменная X обычно носит название независимой переменной (англ. independent variable), переменная Y называется зависимой переменной (англ. dependent variable). Иногда переменную X называют предиктором, переменную Y - откликом. Мы хотим определить именно зависимость от X или предсказать, какими будут значения Y при данных значениях X. В данном случае мы наблюдаем значения X и соответствующие им значения Y. Задача состоит в том, чтобы построить модель, позволяющую по значениям X, отличным от наблюдаемых, определить Y. В статистике подобные задачи решаются в рамках регрессионного анализа.
Существуют различные регрессионные модели, определяемые выбором функции f(x1,x2,…,xm): 1) Простая линейная регрессия
2) Множественная регрессия
3) Полиномиальная регрессия
Коэффициенты
Основная особенность регрессионного анализа: при его помощи можно получить конкретные сведения о том, какую форму и характер имеет зависимость между исследуемыми переменными. Последовательность этапов регрессионного анализа 1. Формулировка задачи. На этом этапе формируются предварительные гипотезы о зависимости исследуемых явлений. 2. Определение зависимых и независимых (объясняющих) переменных. 3. Сбор статистических данных. Данные должны быть собраны для каждой из переменных, включенных в регрессионную модель. 4. Формулировка гипотезы о форме связи (простая или множественная, линейная или нелинейная). 5. Определение функции регрессии (заключается в расчете численных значений параметров уравнения регрессии) 6. Оценка точности регрессионного анализа. 7. Интерпретация полученных результатов. Полученные результаты регрессионного анализа сравниваются с предварительными гипотезами. Оценивается корректность и правдоподобие полученных результатов. 8. Предсказание неизвестных значений зависимой переменной.
При помощи регрессионного анализа возможно решение задачи прогнозирования и классификации. Прогнозные значения вычисляются путем подстановки в уравнение регрессии параметров значений объясняющих переменных. Решение задачи классификации осуществляется таким образом: линия регрессии делит все множество объектов на два класса, и та часть множества, где значение функции больше нуля, принадлежит к одному классу, а та, где оно меньше нуля, - к другому классу.
Основные задачи регрессионного анализа: установление формы зависимости, определение функции регрессии, оценка неизвестных значений зависимой переменной.
Линейная регрессия
Линейная регрессия сводится к нахождению уравнения вида
где x - называется независимой переменной или предиктором. Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y» · a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1). · b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу. · a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b. · e - ненаблюдаемые случайные величины со средним 0, или их еще называют ошибками наблюдений, предполагается что ошибки не коррелированы между собой.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Уравнение вида В большинстве случав (если не всегда) наблюдается определенный разброс наблюдений относительно регрессионной прямой. Теоретической линией регрессии называется та линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию связи. Важным этапом регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Главным основанием для выбора вида уравнения должен служить содержательный анализ природы изучаемой зависимости, ее механизма. Для нахождения параметров а и b уравнения регрессии используем метод наименьших квадратов (МНК). При применении МНК для нахождения такой функции, которая наилучшим образом соответствует эмпирическим данным, считается, что сумма квадратов отклонений (остаток) эмпирических точек от теоретической линии регрессии должна быть величиной минимальной. Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2). Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
После несложных преобразований получим систему нормальных уравнений способа наименьших квадратов для определения величины параметров a и b уравнения прямолинейной корреляционной связи по эмпирическим данным:
Решая данную систему уравнений относительно b, получим следующую формулу для определения этого параметра:
Где Значение параметра а получим, разделив обе части первого уравнения в данной системе на n:
Параметр b в уравнении называют коэффициентом регрессии. При наличии прямой корреляционной зависимости коэффициент регрессии имеет положительное значение, а в случае обратной зависимости коэффициент регрессии – отрицательный. Если знак при коэффициенте регрессии - положительный, связь зависимой переменной с независимой будет положительной. Если знак при коэффициенте регрессии - отрицательный, связь зависимой переменной с независимой является отрицательной (обратной). Коэффициент регрессии показывает, на сколько в среднем изменяется величина результативного признака y при изменении факторного признака х на единицу, геометрический коэффициент регрессии представляет собой наклон прямой линии, изображающей уравнение корреляционной зависимости, относительно оси х (для уравнения
Из-за линейного соотношения Если это так, то большая часть вариации Количественной характеристикой степени линейной зависимости между случайными величинами X и Y является коэффициент корреляции r (Показатель тесноты связи между двумя признаками). Коэффициент корреляции:
где x - значение факторного признака; y - значение результативного признака; n - число пар данных.
Рис.3 - Варианты расположения «облака» точек
Если коэффициент корреляции r=1, то между X и Y имеет место функциональная линейная зависимость, все точки (xi,yi) будут лежать на прямой. Если коэффициент корреляции r=0 (r~0), то говорят, что X и Y некоррелированы, т.е. между ними нет линейной зависимости. Связь между признаками (по шкале Чеддока) может быть сильной, средней и слабой.Тесноту связи определяют по величине коэффициента корреляции, который может принимать значения от -1 до +1 включительно. Критерии оценки тесноты связи показаны на рис. 1.
Любая зависимость между переменными обладает двумя важными свойствами: величиной и надежностью. Чем сильнее зависимость между двумя переменными, тем больше величина зависимости и тем легче предсказать значение одной переменной по значению другой переменной.Величину зависимости легче измерить, чем надежность. Надежность зависимости не менее важна, чем ее величина. Это свойство связано с представительностью исследуемой выборки. Надежность зависимости характеризует, насколько вероятно, что эта зависимость будет снова найдена на других данных. С ростом величины зависимости переменных ее надежность обычно возрастает.
Долю общей дисперсии Коэффициент детерминации измеряет долю разброса относительно среднего значения, которую «объясняет» построенная регрессия. Коэффициент детерминации лежит в пределах от 0 до 1. Чем ближе коэффициент детерминации к 1, тем лучше регрессия «объясняет» зависимость в данных, значение близкое к нулю, означает плохое качество построенной модели.Коэффициент детерминации может максимально приближаться к 1, если все предикторы различны. Разность
Множественная регрессия
Множественная регрессия применяется в ситуациях, когда из множества факторов, влияющих на результативный признак, нельзя выделить один доминирующий фактор и необходимо учитывать влияние нескольких факторов. Например, объем выпуска продукции определяется величиной основных и оборотных средств, численностью персонала, уровнем менеджмента и т. д., уровень спроса зависит не только от цены, но и от имеющихся у населения денежных средств. Основная цель множественной регрессии – построить модель с несколькими факторами и определить при этом влияние каждого фактора в отдельности, а также их совместное воздействие на изучаемый показатель. Множественной регрессией называют уравнение связи с несколькими независимыми переменными:
Где Y – зависимая переменная, x1, x2, xk-1 – независимые переменные (факторные признаки), коэффициенты Постановка задачи множественной регрессии: по имеющимся данным n наблюдений за совместным изменением k-1 параметра Y и xi, i=0,1,…,k-1 необходимо определить аналитическую зависимость Y= f(x1,x2,...,xi), наилучшим образом описывающую данные наблюдений. Регрессионный анализ простой линейной регрессии обобщается на случай множественной регрессии. Для нахождения оценок параметров
12 |



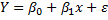


 называются параметрами регрессии.
называются параметрами регрессии. или
или  . (1.1)
. (1.1)

 . (1.2)
. (1.2) (1.3)
(1.3) и
и  - средние значения y, x.
- средние значения y, x. (1.4)
(1.4) и
и  мы ожидаем, что
мы ожидаем, что 


 представляет собой процент дисперсии, который нельзя объяснить регрессией.
представляет собой процент дисперсии, который нельзя объяснить регрессией. свободный член.
свободный член. , i=0,1,…,k-1 по результатам наблюдений используется метод наименьших квадратов (МНК).
, i=0,1,…,k-1 по результатам наблюдений используется метод наименьших квадратов (МНК).