 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Алгебраїчні критерії стійкості
Поняття стійкості системи
Під стійкістю системи розуміється здатність її повертатися до стану сталої рівноваги після зняття збурення, що порушило цю рівновагу. Нестійка система безперервно віддаляється від рівноважного стану або здійснює навколо нього коливання із зростаючою амплітудою.
Стійкість лінійної системи визначається не характером збурення, а структурою самої системи (рис.61). Говорять, що система стійка "в малому", якщо визначений факт наявності стійкості, але не визначені її межі. Система стійка "у великому", коли визначені межі стійкості і те, що реальні відхилення не виходять за ці межі. Відповідно до класичного методу розвязок диференціального рівняння записується у вигляді:
Хвих(t)= Хвих вим(t)+ Хвих п (t).
Тут Хвих п (t) - загальне рішення однорідного диференціального рівняння, тобто рівняння з нульовою правою частиною:
an хвих (n)+ an-1 хвих (n-1) + ... + а1 хвих + а(0) хвих = 0.
Фізично це означає, що всі зовнішні дії зняті і система абсолютно вільна, її рухи визначаються лише власною структурою. Тому розв'язок даного рівняння Хвих п (t) називається (перехідною) вільною складовою загального розв'язку. Хвих вим(t)– частковий розв'язок неоднорідного диференціального рівняння, під яким розуміється рівняння з ненульовою правою частиною. Фізично це означає, що до системи прикладено зовнішню дію u(t). Тому друга складова загального розв'язку називається вимушеною. Вона визначає вимушений усталений режим роботи системи після закінчення перехідного процесу.
Можна провести аналогію між САУ і пружиною, коливання якої описуються диференціальним рівнянням аналогічним (рис.62). Відтягнемо пружину, а потім відпустимо. Пружина коливатиметься відповідно до вільної складової розв'язку рівняння, тобто характер коливань визначатиметься тільки структурою самої пружини. Якщо у момент часу t= 0підвісити до пружини вантаж, то на вільні коливання накладеться зовнішня сила Р. Після загасання коливань, що описуються тільки вільною складовою загального розв'язку, система перейде в новий сталий режим, що характеризується вимушеною складовою Хвих вим = Хвих(t Кожна складова загального розв'язку рівняння динаміки шукається окремо. Вимушена складова шукається на основі рішення рівняння статики для даної системи для часу t
Кожному від'ємному дійсному кореню відповідає експоненціально затухаюча в часі складова Хвих.п(t)i, кожному позитивному - що експоненціально розходиться, кожному нульовому кореню відповідає
Оскільки після зняття збурення Хвих вим(t) = 0, то стійкість системи визначається тільки характером вільної складової Хвих п(t). Тому умова стійкості систем за Ляпуновим формулюється так: у стійкій системі вільна складова розв'язку рівняння динаміки, записаному у відхиленнях, повинна прямувати до нуля, тобто загасати.
Виходячи з розташування на комплексній площині корені з від'ємною дійсною частиною називаються лівими, з додатними - правими (рис.65). Тому умову стійкості лінійної САУ можна сформулювати таким чином: для того, щоб система була стійка, необхідно і достатньо, щоб всі корені її характеристичного рівняння було лівими. Якщо хоч би один корінь правий, то система нестійка. Якщо один з коренів рівний нулю (у системах, де a0 = 0), а решта лівих, то система знаходиться на межі аперіодичної стійкості. Якщо рівні нулю дійсні частини однієї або декількох пар комплексно зв'язаних коренів, то система знаходиться на межі коливальної стійкості. Правила, що дозволяють судити про знаки коренів характеристичного рівняння без його рішення, називаються критеріями стійкості. Їх можна розділити на алгебраїчні (засновані на складанні по даному характеристичному рівнянню за певними правилами виразів алгебри, по яких можна судити про стійкість САУ) і частотні (засновані на дослідженні частотних характеристик).
Алгебраїчні критерії стійкості
Необхідна умова стійкості
Характеристичне рівняння системи за допомогою теореми Вієта може бути записано у вигляді
D(s)= ansn + an-1sn-1 + an-2sn-2 + ... + a0 = аn(s-s1)(s-s2) ...(s-sn)= 0
де s1, s2, ..., sn- корені цього рівняння. Якщо система стійка, означає все корені ліві, тобто дійсні частини всіх коренів від'ємні, що можна записати як ai = -|ai| < 0. Підставимо їх в рівняння:
an
Перемножуючи комплексно зв'язані вирази, одержимо:
an
Після розкриття дужок отримаємо вираз
an
Оскільки в дужках немає жодного від'ємного числа, то жоден з коефіцієнтів a0,a1,...,an не буде від'ємним. Тому необхідною умовою стійкості САУ є додатність всіх коефіцієнтів характеристичного рівняння: an > 0, Розглянута умова є необхідною, але не достатньою умовою. Необхідні і достатні умови дають алгебраїчні критерії Рауса і Гурвіця.
Критерій Рауса
Раус запропонував критерій стійкості САУ у вигляді алгоритму, по якому заповнюється спеціальна таблиця з використанням коефіцієнтів характеристичного рівняння. Для дослідження потрібно мати характеристичне рівняння замкнутої системи.Нехай характеристичне рівняння має вигляд: ansn+ an-1sn-1+ an-2sn-2+ …a1s+a0 = 0 Складаємо таблицю Рауса.
Якщо нема наступних коефіцієнтів, то заповнюємо визначник нулями.
Кількість рядків таблиці n+1, де n-показник степеня характеристичного рівняння. Критерій Рауса полягає в наступному: для стійкості системи потрібно, щоб кожний перший елемент першого стовпчика таблиці був більшим від 0, тобто додатним. Якщо це не виконується, то система нестійка, а кількість правих коренів рівна числу змін знаку в першому стовпці. Приклад: a3s3+a2s2+a1s+a0=0
Для системи 3-го порядку: для стійкості крім необхідної умови потрібно, щоб різниця добутків середніх і крайніх членів була більшою від нуля. Перевага - критерій простий у використанні незалежно від порядку характеристичного рівняння. Його недолік - мала наочність, важко судити про ступінь стійкості системи, на скільки далеко знаходиться вона від границі стійкості.
Критерій Гурвіця
Гурвіц запропонував інший критерій стійкості. З коефіцієнтів характеристичного рівняння будується визначник Гурвіця згідно алгоритму: 1) по головній діагоналі зліва направо виставляються всі коефіцієнти характеристичного рівняння починаючи від другого коефіцієнту an-1 до a0; 2) від кожного елементу діагоналі вгору і вниз добудовуються стовпці визначника так, щоб індекси збільшувалися зверху вниз; 3) при відсутності коефіцієнта (на місце коефіцієнтів з індексами менше нуля або більше за n) ставляться нулі.
Критерій Гурвіця: а) необхідна умова стійкості: всі коефіцієнти характеристичного рівняння замкненої системи повинні бути більшими від нуля (додатними); б) достатня умова стійкості: для того, щоб САК була стійка, необхідно і достатньо, щоб всі n діагональні мінори визначника Гурвіця були додатними.
Розглянемо приклади застосування критерію Гурвіця: 1) n = 1 => рівняння динаміки: a1s + a0 = 0. Визначник Гурвіця: 2)n = 2 => рівняння динаміки: a2s2 + a1s + a0 = 0. Визначники Гурвіця: 3) n = 3 => рівняння динаміки: a3s3 + a2s2 + a1s + a0 = 0. Визначники Гурвіця: D1 = a1 > 0 D2 = a2a1 - a0a3 > 0; D3 = a0D2 > 0, умова стійкості: a0 > 0; a1 > 0; a2 > 0; a3 > 0; a1a2 - a0a3 > 0; Таким чином при n Критерій Гурвіця застосовують при n
Критерію Гурвіця часто використовують для визначення впливу одного з параметрів САУ на її стійкість. Так рівність нулю головного визначника Dn = a0
|






 ). Якщо зовнішня дія сама змінюється за синусоїдальним законом P = Posin(wt + j), то після загасання перехідного процесу система здійснюватиме вимушені коливання з тією ж частотою, що і зовнішня дія, тобто Хвих вим(t) = Хвих вим max sin(wt + j).
). Якщо зовнішня дія сама змінюється за синусоїдальним законом P = Posin(wt + j), то після загасання перехідного процесу система здійснюватиме вимушені коливання з тією ж частотою, що і зовнішня дія, тобто Хвих вим(t) = Хвих вим max sin(wt + j). де siкорені характеристичного рівняння D(s)= an s (n)+ an-1 s (n-1) + ... + s1 хвих + s0 = 0. Корені можуть бути або дійсними si = ai, або попарно комплексно зв'язаними si = ai ± jwi. Постійні ciвизначаються виходячи з початкових і кінцевих умов, підставляючи в загальне рішення значення u, уі їх похідні в моменти часу t = 0і t
де siкорені характеристичного рівняння D(s)= an s (n)+ an-1 s (n-1) + ... + s1 хвих + s0 = 0. Корені можуть бути або дійсними si = ai, або попарно комплексно зв'язаними si = ai ± jwi. Постійні ciвизначаються виходячи з початкових і кінцевих умов, підставляючи в загальне рішення значення u, уі їх похідні в моменти часу t = 0і t 


 (s + |a1|)
(s + |a1|)  2)
2) 




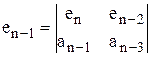 ,
,  ,
,  .
. .
.

 ;
; ; …..
; ….. 
 . Враховуючи це, умова стійкості: a2 > 0, a1 > 0, a0 > 0;
. Враховуючи це, умова стійкості: a2 > 0, a1 > 0, a0 > 0; 2додатність коефіцієнтів характеристичного рівняння є необхідною і достатньою умовою стійкості САУ. При n > 2з'являються додаткові умови.
2додатність коефіцієнтів характеристичного рівняння є необхідною і достатньою умовою стійкості САУ. При n > 2з'являються додаткові умови.
 n-1 = 0говорить про те, що система знаходиться на межі стійкості. При цьому або a0 = 0- при виконанні решти умов система знаходиться на межі аперіодичної стійкості, або передостанній мінор
n-1 = 0говорить про те, що система знаходиться на межі стійкості. При цьому або a0 = 0- при виконанні решти умов система знаходиться на межі аперіодичної стійкості, або передостанній мінор