 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Коефіцієнт статичної похибки
Загальні положення. Розділ статика займається дослідженням систем в усталеному режимі, що виникає після завершення всіх перехідних процесів. Основною характеристикою статики окремої ланки системи є характеристика вхід-вихід хвих = f(хвх). Важливим показником ланки є статичний коефіцієнт передачі к = хвих/хвх. Залежно від того, яким чином підтримується сталою регульована величина САР після закінчення перехідного процесу, з позицій статики визначають два основних види САР: статичні і астатичні. Основна задача статики – визначити похибку регулювання вихідної величини. Статичні похибки параметрів.
Показник, що характеризує якість системи в статиці, називається статичною точністю. Статична похибка – це відхилення регульованої величини від заданого значення після закінчення перехідного процесу. Вона є одним із основних показників якості САР. Якщо головного зворотного зв'язку ГЗЗ в системі нема (САК знаходиться в розімкнутому стані),то при початковому значенні збурення f0(t) вихідна величина об'єкта х0вих відповідатиме потрібному значенню регульованої величини. Зміна збурення до значення f1(t) призведе до зміни вихідної величини об'єкта до значення х1вихі появи відхилення при розімкнутому стані системи Dх = х0вих – х1вих. Якщо замкнути систему за допомогою головного зворотного зв'язку то в замкнутій системі регулятор Р діятиме на зменшення відхилення. Dх (в ідеальному випадку до нуля). Проте регулятор не в змозі повністю ліквідувати Dх, а зменшуватиме його на деяку величину, яку позначимо Dхвих. Частина Dх, яка залишається в замкнутій системі, є статичною похибкою замкнутої системи: D=Dх - Dхвих. Величина D надходить знову на вхід об’єкта, тому можна записати D=Dхвх.
Розділивши всі члени рівняння на величину D і врахувавши вираз (2.12), дістанемо 1 = Dх/D - Dхвих/Dхвх. Оскільки Dхвих/Dхвх= к - коефіцієнт передачі (підсилення) розімкнутої системи, то статичну похибку замкнутої системи запишемо у вигляді D = Dх/(1+к) З цієї формули можна зробити такі висновки. 1. Статична похибка замкнутої системи прямо пропорційна відхиленню регульованої величини при розімкнутому стані системи і і обернено пропорційна коефіцієнту підсилення розімкнутої системи. 2. Оскільки величина Dхпри розімкнутій системі є функцією збурення, що діє на об'єкт, то статична похибка замкнутої системи залежить від збурення. Як буде показано далі при дослідженнях САР, зростання коефіцієнта передачі розімкнутої системи погіршує динамічні властивості (зменшує так званий запас стійкості системи). Тому бажання зменшити похибку замкнутої системи за рахунок зростання коефіцієнта передачі може призвести до втрати стійкості САР. Це відображає суперечність між вимогами статики та динаміки і веде до необхідності компромісного узгодження вимог статичної точності і стійкості САР. Неможливість задоволення вимог статики і динаміки при деякій прийнятій САР веде до необхідності зміни її структури. Статична похибка САК при комбінованому керуванні. При комбінованому керуванні функціональна схема має дві частини. Одна - це замкнутий контур об'єкт (О) + регулятор (Р), який забезпечує регулювання за відхиленням, а друга — розімкнутий (компенсаційний) канал К, який формує компенсаційний сигнал на об'єкті керування (рис.2.8). За допомогою компенсаційного сигналу в комбінованій системі реалізується також принцип керування за збуренням. Якщо розімкнути замкнутий контур на виході об'єкта, то відхилення вихідної величини об'єкта при дії компенсаційного каналу обчислюється за формулою Dхвих* = х0вих – х1вих - хк,
де х0вих — початкове значення регульованої величини, що дорівнює заданому; х1вих — нове значення вихідної величини об'єкта, яке відповідає зміні збурення; хк — компенсаційна дія розімкнутого каналу. Відхилення Dхвихк буде значно меншим від відхилення при відсутності компенсаційного каналу Dхвихк < Dхвих. Тому статична похибка комбінованої САК
Dк = Dхвихк/(1+к) буде менша за похибку замкнутої САК Dк <D = Dхвих/(1+к).
Випадок 1. Нехай загальний коефіцієнт рівний добутку коефіцієнтів
Вважаємо, що в системі параметри к1 і к2 можуть змінюватися (δк1,δк2). Зміна параметрів може характеризуватися двома випадками: а) (основний) Причини, що спричиняють похибки окремих величин, незалежні. В цьому випадку необхідно підставляти такі знаки, щоб мати максимальне значення dк. б) (рідко зустрічається) Причини, що приводять до похибок взаємозв'язані. В цьому випадку при розрахунку сумарної похибки треба представляти складові похибки з таким знаком, який диктується цими причинами.
lnк = n1lnк1+n2lnк2;
dк=n1dк1+n2dк2 Якщо
При використанні формул значення похибки треба брати такі, що відповідають причинам виникнення цих похибок. 2. Випадок 2.
к=к1+к2 lnк=ln(к1+к2)
Якщо
Розглянемо приклади: Приклад 1 к=5к1к22 У всіх випадках використовується випадок а (причина незалежна) dк1=±2% dк=dк1+2dк2=2%±2×3%=8% dк2=±3% dк=±8% dк=? Приклад 2
dк1=±2% dк=1/2 dк1-3×dк2=1%+3%=4% dк2=±1% dк=±4% dк=? Приклад 3
dк1=±2% dк2=±1% к=к1*+к2* к1=25 к2=1 dк=? dк1*=1/2dк1 dк2*= -dк2 dк=5/4×1/2dк1-1/4dк2=1,25×1/2dк1+0,25dк2=1,25%+0,25%=1,5% dк=±1,5%
Коефіцієнт статичної похибки
Статична точність роботи системи характеризується величиною як коефіцієнт статичної похибки.
Відношення абсолютної похибки Dхвих до значення, яке необхідно мати хвих. |




 ; Замінимо з певною точністю
; Замінимо з певною точністю ;
;

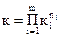


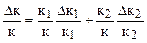

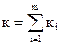 то
то 
 к=-к11/2×к2-3
к=-к11/2×к2-3





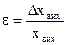 (2.1)
(2.1)