 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основні теореми диференціального числення
ЛЕКЦІЯ 7. ДИФЕРЕНЦІАЛ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ. Основні теореми диференціального числення ПЛАН 1. Означення диференціалу функції 2. Застосування деференціала в наближених обчисленнях 3. Правила знаходження диференціала 4. Основні теореми диференціального числення
Означення диференціалу функції Нехай функція у = f (х) диференційовна на деякому проміжку, тобто для будь-якої точки х з цього проміжку границя Враховуючи взаємозв’язок змінної величини, що має скінченну границю, і нескінченної малої величини, можемо записати Помноживши всі члени останньої рівності на
З виразу (1) випливає, що приріст функції Означення 1. Добуток
Знайдемо диференціал функції у = х; для цього випадку
Приклад. Знайти диференціал dy функції 1) 2) якщо х = 20, Приклад. Знайти диференціал dy функції Оскільки
Застосування деференціала в наближених обчисленнях Вираз (2) з урахуванням (3) можна записати так:
Якщо При малих
Остання наближена рівність тим точніша, чим менше Приклад. Обчислити наближено Перетворимо вираз, що стоїть під знаком радикала:
При обчисленні Формула (5) у нашому випадку запишеться так:
Інакше
Підставивши (7) у рівність (6), дістанемо
Правила знаходження диференціала Застосовуючи формулу похідної та властивості похідних, дістаємо правила знаходження диференціала: 1. у = с; dy = 0; 3. 2. Теорема. Форма диференціала не залежить від того, чи є аргумент незалежною змінною або функцією. Основні теореми диференціального числення Теорема Ферма. Якщо диференційовна на проміжку Припустимо, для визначеності, що За означенням похідної
причому ця границя не залежить від того, як наближається Розглянемо відношення Для всіх х, достатньо близьких до точки
Перейдемо в останніх нерівностях до границі при
Аналогічно розглядається випадок, коли функція Геометричний зміст теореми Ферма. Геометричний зміст похідної Теорема Ролля. Якщо функція f (х): 1) неперервна на сегменті [a; b]; 2) диференційовна на інтервалі (а; b); 3) на кінцях сегмента набуває рівних між собою значень, тобто f (a) = f (b), то на інтервалі (а; b) існує хоча б одна точка Геометричний зміст теореми Ролля.Якщо крайні ординати неперервної кривої у = f (х), яка має в кожній точці дотичну, рівні, то на цій кривій знайдеться принаймні одна точка з абсцисою
Рис. 6 Теорема Лагранжа (теорема про скінченні прирости функції). Якщо функція f (х): 1) неперервна на сегменті [a; b]; 2) диференційовна на інтервалі (а; b), то на інтервалі знайдеться хоча б одна точка
Геометричний зміст теореми Лагранжа. Запишемо формулу (8) у вигляді
З рис. 4.7 бачимо, що величина
Рис. 7 Водночас, Теорема Коші. Якщо f (x) і
|
 існує і дорівнює скінченному числу.
існує і дорівнює скінченному числу. , де
, де  — нескінченно мала величина (
— нескінченно мала величина (  при
при  ).
). , дістанемо
, дістанемо . (1)
. (1) складається із суми двох доданків, з яких перший доданок — так звана головна частина приросту, лінійна відносно
складається із суми двох доданків, з яких перший доданок — так звана головна частина приросту, лінійна відносно 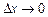 добуток
добуток  є нескінченно мала величина першого порядку відносно
є нескінченно мала величина першого порядку відносно  ). Другий доданок — добуток
). Другий доданок — добуток  завжди нескінченно мала величина вищого порядку, ніж
завжди нескінченно мала величина вищого порядку, ніж  (2)
(2) , отже,
, отже,  . Таким чином, диференціал незалежної змінної збігається з її приростом
. Таким чином, диференціал незалежної змінної збігається з її приростом  . (3)
. (3) : 1) при довільних значеннях х та
: 1) при довільних значеннях х та  ;
; .
. .
. , то за формулою (3) дістанемо
, то за формулою (3) дістанемо .
. . (4)
. (4) , то величина
, то величина 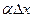 є малою величиною вищого порядку порівняно з dy.
є малою величиною вищого порядку порівняно з dy. доданком
доданком  , або в розгорнутому вигляді:
, або в розгорнутому вигляді: 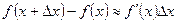 , звідки
, звідки . (5)
. (5) .
. , звідки
, звідки  . (6)
. (6) введемо функцію
введемо функцію  , тоді
, тоді  .
. , де
, де  .
. . (7)
. (7) .
.
 ; 4.
; 4.  .
.
 досягає найбільшого або найменшого значення у внутрішній точці
досягає найбільшого або найменшого значення у внутрішній точці  цього проміжку, то похідна функції в цій точці дорівнює нулю, тобто
цього проміжку, то похідна функції в цій точці дорівнює нулю, тобто 
 набуває в точці
набуває в точці  найбільшого значення, тобто для всіх
найбільшого значення, тобто для всіх 
 .
. ,
, до
до 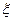 — справа чи зліва.
— справа чи зліва. .
. , маємо:
, маємо: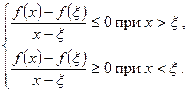
 . Дістанемо
. Дістанемо .
. набуває в точці
набуває в точці  найменшого значення.
найменшого значення. являє собою кутовий коефіцієнт дотичної до кривої
являє собою кутовий коефіцієнт дотичної до кривої  . Звідси рівність нулю похідної
. Звідси рівність нулю похідної  геометрично означає, що у відповідній точці цієї кривої дотична паралельна осі Ох.
геометрично означає, що у відповідній точці цієї кривої дотична паралельна осі Ох. , для якої
, для якої 
 , в якій дотична паралельна осі Ох (рис. 6).
, в якій дотична паралельна осі Ох (рис. 6).
 , така що
, така що (8)
(8) . (9)
. (9) є тангенсом кута
є тангенсом кута  нахилу хорди, що проходить через точки А і В графіка функції
нахилу хорди, що проходить через точки А і В графіка функції
 — тангенс кута нахилу дотичної до кривої у точці С з абсцисою
— тангенс кута нахилу дотичної до кривої у точці С з абсцисою  дві функції: 1) неперервні на сегменті [a; b]; 2) диференційовні на інтервалі (а; b); 3)
дві функції: 1) неперервні на сегменті [a; b]; 2) диференційовні на інтервалі (а; b); 3)  для
для  , то на інтервалі (а; b) знайдеться хоча б одна точка
, то на інтервалі (а; b) знайдеться хоча б одна точка 