 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Рівняння дотичної і нормалі до плоскої кривої
ЛЕКЦІЯ 5-6. ПОХІДНА ФУНКЦІЇ ПЛАН 1. Означення похідної 2. Геометричний зміст похідної 3. Механічний зміст похідної 4. Рівняння дотичної і нормалі до плоскої кривої 5. Залежність між неперервністю і диференційованістю функції 6. Основні правила диференціювання 7. Похідні від основних елементарних функцій 8. Похідні вищих порядків
Означення похідної Нехай функція
Якщо границя (1) існує і скінченна, вона називається похідною функції
Означення 1. Похідною функції Операція знаходження похідної називається диференціюванням цієї функції. Користуючись означенням похідної, знайти похідні функцій. Приклад. Функція у = х2. Знайти похідну в точках х = 3 і х = – 4. Надамо аргументу х приросту Складемо відношення приросту функції до приросту аргументу Похідна в точці х = 3 Приклад. Надавши аргументу
Приклад. Користуючись відомою з тригонометрії формулою
знайдемо приріст функції у точці
Аналогічно можна дістати: Приклад. Для цієї функції маємо
тобто Геометричний зміст похідної Означення 2. Дотичною до кривої L у точці М називається граничне положення МN січної ММ1 при прямуванні точки М1 по кривій L до точки М (рис. 1). Нехай крива, задана рівнянням З Таким чином,
Рис. 1 Рис.2 Оскільки Механічний зміст похідної Припустимо, що точка М рухається прямолінійно нерівномірно по деякій прямій лінії, яку візьмемо за вісь Ох (рис. 3).
Рух точки відбувається за законом х = f (t), де х — шлях; t — час. Знайдемо швидкість точки М у даний момент часу t (миттєва швидкість). Нехай точка М у момент t перебувала на відстані х від початкової точки М0, а в момент часу Якщо точка М рухається рівномірно, то Vcр є величина стала, і її беруть за швидкість точки. Для нерівномірного руху точки очевидно, що для достатньо близьких значень
яка є швидкістю зміни функції х = f (t) у точці. У цьому полягає механічний зміст похідної. Рівняння дотичної і нормалі до плоскої кривої Нехай функція у=f(t) означена і неперервна на деякому проміжку [a; b]. Визначимо рівняння дотичної й нормалі до графіка функції у = f (x) у точці з абсцисою Оскільки дотична й нормаль проходять через точку з абсцисою х0, то рівняння кожної з них будемо шукати у вигляді рівняння прямої, що проходить через задану точку М0 (х0; у0) у даному напрямі (рис. 4):
де k кутовий коефіцієнт дотичної. Використовуючи геометричний зміст похідної, маємо
Рис. 4 Рівняння дотичної.Оскільки
Рівняння нормалі.Означення. Нормаллю до графіка функції в точці М0 називається перпендикуляр, проведений до дотичної в цій точці (рис. 4). Використовуючи умову перпендикулярності дотичної та нормалі, знаходимо кутовий коефіцієнт нормалі
Приклад. Знайти рівняння дотичної та нормалі до графіка функції у = х2 у точці з абсцисою х0=–3. Знайдемо похідну від заданої функції Рівняння дотичної (3) і нормалі (4) запишуться так: |



 визначена на деякому проміжку (а; b). Візьмемо значення
визначена на деякому проміжку (а; b). Візьмемо значення  і надамо аргументу приросту
і надамо аргументу приросту  . Тоді функція набуде приросту
. Тоді функція набуде приросту 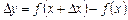 . Розглянемо відношення приросту функції
. Розглянемо відношення приросту функції  до приросту аргументу
до приросту аргументу 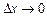 :
: . (1)
. (1) .
.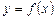 за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля. , тоді функція набуде приросту
, тоді функція набуде приросту 
 , відшукаємо границю
, відшукаємо границю  . Таким чином,
. Таким чином,  .
. , а похідна при х = – 4 буде
, а похідна при х = – 4 буде  .
. , де
, де  .
. приросту
приросту  . Тепер знайдемо границю відношення
. Тепер знайдемо границю відношення  при
при  :
: , тобто
, тобто 
 .
. ,
, ,
, ;
;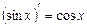 .
. .
. .
. ,
, .
. . Надамо в точці х приросту
. Надамо в точці х приросту  випливає, що
випливає, що  . Коли
. Коли 
 і січна прямує до положення дотичної МN.
і січна прямує до положення дотичної МN. .
.

 , то
, то  тобто похідна
тобто похідна  чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х. У цьому полягає геометричний зміст похідної.
чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х. У цьому полягає геометричний зміст похідної. Рис. 3
Рис. 3 точка опинилася на відстані
точка опинилася на відстані  від початкової точки й зайняла положення М1. Отже, час t набув приросту
від початкової точки й зайняла положення М1. Отже, час t набув приросту  , а шлях х — приросту
, а шлях х — приросту  . Середня швидкість руху точки М за час
. Середня швидкість руху точки М за час 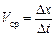 .
. ,
, .
. , (2)
, (2) .
.
 , то з виразу (2) дістанемо рівняння дотичної у вигляді
, то з виразу (2) дістанемо рівняння дотичної у вигляді . (3)
. (3) і записуємо її рівняння у вигляді
і записуємо її рівняння у вигляді . (4)
. (4) .
. або у загальному вигляді: 6х+у+9=0, х–6у+57=0.
або у загальному вигляді: 6х+у+9=0, х–6у+57=0.