 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение опорных моментов в загруженном пролете способом моментных фокусов
Моментные фокусные отношения
Рассмотрим неразрезную балку, загруженную заданной нагрузкой только в одном пролете и известным нам способом построим эпюру изгибающих моментов (схематично показана на рис. 5.1). Обратим внимание на особенность приведенной эпюры – наличие точек нулевых значений моментов в незагруженных пролетах. Они расположены слева и справа от загруженного пролета. Назовем их левыми и правыми моментными фокусами: – левым (правым) моментным фокусом называется нулевая точка эпюры моментов в пролете при действии нагрузки справа (слева) от него.
Вполне очевидно, что если N существует, то влияния на характер и величину изгибающего момента не окажет. Поперечная сила Q приложена на опоре и тоже не окажет влияния на изгибающий момент. Таким образом, изгибающие моменты в рассматриваемых пролетах будут зависеть только от величины опорного момента M2. Учитывая, что в рассматриваемых пролетах закон изменения изгибающего момента линеен, то как бы не менялось значение опорного момента M2, величина момента в пролетах изменяется пропорционально и положение моментных точек не изменится. Естественно, что сказанное справедливо и для правых моментных точек.
Различают левое и правое фокусные отношения: – левое – правое Рассмотрим два соседних незагруженных пролета (рис. 5.4) в предположении, что нагрузка справа.
Разделим записанное уравнение на Mn:
Так как ранее было принято, что
Перепишем уравнение 3-х моментов с учетом введенных обозначений:
Найдем
Получили рекуррентную формулу вычисления левых фокусных отношений. Чтобы воспользоваться ей, надо знать хотя бы одно фокусное отношение. Рассмотри крайний левый пролет с шарнирным опиранием (рис. 5.5). Найдем левое фокусное отношение для первого пролета:
Тогда фокусное отношение для второго пролета, при условии, что он не загружен:
Рассмотрим случай, когда крайний левый пролет имеет левую опору в виде защемления (рис. 5.6). Заменим защемление нулевым пролетом бесконечной жесткости. Учтем, что для нулевого пролета
Вполне верно будет обобщить полученные результаты на правые фокусные отношения. Рекуррентная формула:
Для крайних правых незагруженных пролетов, в зависимости от типа опирания, справедливы ранее полученные результаты.
Определение опорных моментов в загруженном пролете способом моментных фокусов
Применим фокусные отношения к определению опорных моментов в загруженном пролете (рис. 5.7). Запишем уравнение 3-х моментов для n-1 и n опор:
Учтем фокусные отношения:
Перепишем первое уравнение 3-х моментов:
Обратим внимание, что
По аналогии можем записать второе уравнение 3-х моментов (для n–й опоры):
Разрешив совместно первое и второе уравнение относительно опорных моментов Mn-1 и Mn, получим:
|




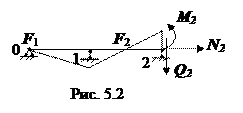 Рассмотрим, влияет ли характер и величина нагрузки на положение моментных фокусов. Для этого проведем сечение через левую опору загруженного пролета и рассмотрим равновесие левой же отсеченной части (рис. 5.2). Влияние правой отсеченной части заменим известными усилиями M, Q и N.
Рассмотрим, влияет ли характер и величина нагрузки на положение моментных фокусов. Для этого проведем сечение через левую опору загруженного пролета и рассмотрим равновесие левой же отсеченной части (рис. 5.2). Влияние правой отсеченной части заменим известными усилиями M, Q и N. Моментным фокусным отношением назовем отношение между опорными моментами какого-либо незагруженного пролета (рис. 5.3).
Моментным фокусным отношением назовем отношение между опорными моментами какого-либо незагруженного пролета (рис. 5.3). , если загружен пролет справа;
, если загружен пролет справа; , если загружен пролет слева.
, если загружен пролет слева.
 .
. .
. ,
,  .
.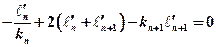 .
.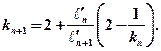

 .
. и т.д..
и т.д.. . Получим:
. Получим: .
.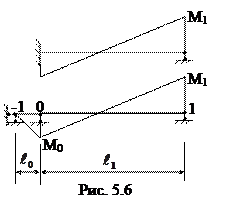 Далее можно вычислить фокусные отношения для всех незагруженных левых пролетов.
Далее можно вычислить фокусные отношения для всех незагруженных левых пролетов.

 .
. , откуда
, откуда  ;
;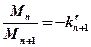 , откуда
, откуда 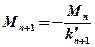
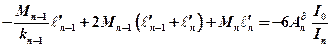 , или, приведя подобные и проведя необходимые преобразования:
, или, приведя подобные и проведя необходимые преобразования: .
.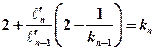 и первое уравнение примет следующий вид:
и первое уравнение примет следующий вид: .
. .
. ,
, .
.