 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Порядок расчета неразрезных балок
Выбор основной системы Как известно, для обеспечения геометрической неизменяемости плоского стержня (жесткого диска) требуется три опорных стержня, оси которых не параллельны друг другу и не пересекаются в одной точке. Тогда количество «лишних» связей можно найти по следующей формуле: W = C0 – 3, где С0 – количество простых опорных стержней. Для балки на рис. 4.1 степень статической неопределимости будет: W = C0 – 3 = 6 – 3 = 3. При выборе основной системы метода сил основными критериями оптимального выбора является минимум вычислений при определении коэффициентов dij и DiP, простота канонических уравнений – часть dij и DiP равны нулю. Рассмотрим следующие две основные системы для балки, показанной на рис. 4.1: 1. Отбросим «лишние» связи, причем не важно какие, лишь бы обеспечить геометрическую неизменяемость – все основные системы получаться типовыми по принципу замены «лишних» связей неизвестными усилиями (рис. 4.2).
В этом случае, как видно из схематично приведенных эпюр от единичных неизвестных, все dij ≠ 0. Такая основная система не может считаться рациональной.
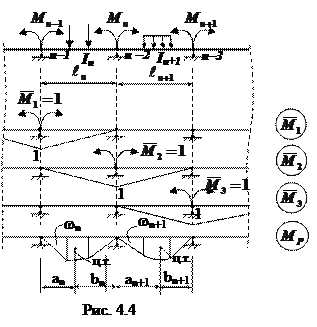
Уравнение трех моментов Нами установлено, что при выборе основной системы метода сил для неразрезной балки путем врезания опорных шарниров, все dij при |i – j| ≥ 2 равны нулю. Тогда в каждом каноническом уравнении метода сил войдут не более трех неизвестных, которыми являются опорные моменты Мi. Для некоторой опоры n каноническое уравнение отражает отсутствие взаимного поворота стержней слева и справа на ней:
Получим:
Вычислим свободный член DiP:
Произведение
Действительно, wn – площадь эпюры МР или, с другой стороны, равнодействующая распределенной нагрузки, изменяющейся по закону изменения изгибающего момента МР в пролете n. Аналогично
Тогда
Запишем каноническое уравнение для n–й опоры с учетом найденных коэффициентов при неизвестных усилиях и свободного члена:
Умножим записанное выражение на 6EIn и введем следующие обозначения:
Перепишем каноническое уравнение с учетом введенных обозначений:
Получили уравнение трех моментов, рекуррентную формулу, позволяющую достаточно формально записать систему канонических уравнений для неразрезной балки. Когда моменты инерции всех пролетов одинаковы, то уравнение 3–х моментов упрощается:
Для наиболее часто встречающихся нагрузок фиктивные опорные реакции вычислены и сведены в таблицы, которые приведены в большинстве учебников по строительной механике (см. приложение 1). Из анализа уравнения 3–х моментов следует: – неразрезные балки из разных материалов испытывают одни и те же усилия при прочих равных условиях работы; – опорные моменты зависят не от абсолютных значений моментов инерции, а от их соотношений в пролетах, тем самым наглядно подтверждается свойство статически неопределимых систем о перераспределении внутренних усилий пропорционально жесткостям стержней. Порядок расчета неразрезных балок 1. Определяется степень статической неопределимости по формуле W = C0 – 3 и формируется основная система метода сил путем введения шарниров во все промежуточные опоры. Все опоры нумеруются слева направо начиная с 0.
Если балка одним концом защемлена, то защемление заменяется нулевым пролетом бесконечной жесткости (рис. 4.5 а). Консоль заменяется опорным моментом, который при любом нагружении консоли не сложно вычислить (рис. 4.5 б). 2. Для каждой промежуточной опоры записывается уравнение трех моментов:
3. Находятся приведенные длины 4. Из решения системы канонических уравнений в форме 3–х моментов находим искомые опорные моменты Mn.
– аналитически по формуле
– графически, путем сложения эпюры MP и эпюры от опорных моментов. 6. Проводится деформационная проверка, для чего строятся вспомогательные эпюры изгибающих моментов от единичных неизвестных (вполне достаточно одной):
7. Эпюра поперечных сил строится по известной нам формуле
8. Определяются опорные реакции Rn, вырезая опоры замкнутым сечением и загружая сечения опорными поперечными силами слева и справа. 9. Проводится статическая проверка равновесия балки:
Удостоверившись, что проверки выполняются, расчет балки считается завершенным. |





 .
.
 ,
,
 .
. .
. можно трактовать как правую опорную реакцию опоры n (в пролете n) –
можно трактовать как правую опорную реакцию опоры n (в пролете n) –  :
: .
. – левая фиктивная опорная реакция n–й опоры (в пролете n+1).
– левая фиктивная опорная реакция n–й опоры (в пролете n+1). .
. .
.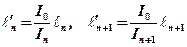 – соответственно, приведенные длины пролетов n и n+1.
– соответственно, приведенные длины пролетов n и n+1. .
.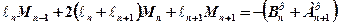 .
.

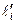 , если пролеты обладают различной жесткостью и фиктивные опорные реакции
, если пролеты обладают различной жесткостью и фиктивные опорные реакции  и
и  для всех промежуточных опор.
для всех промежуточных опор. 5. Эпюру изгибающих моментов (рис. 4.6) можно построить двумя способами (один будет проверочным):
5. Эпюру изгибающих моментов (рис. 4.6) можно построить двумя способами (один будет проверочным): ;
; .
. .
.