 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Порядок расчета статически неопределимых рам методом сил.
Основные понятия о статически неопределимых стержневых системах. Их свойства. Методы расчета. Статически неопределимыми стержневыми системами назовем такие, для расчета которых недостаточно одних уравнений равновесия. Другими словами, статически неопределимыми системами являются те, на которые наложено большее число связей, чем необходимо с точки зрения обеспечения геометрической неизменяемости. Различают два основных типа статически неопределимых систем – внешне и внутренне статически неопределимые. Конечно, возможен случай, когда стержневая система статически неопределима внешне и внутренне, т.е. смешанная. Внешне статически неопределимой системой является та стержневая система, на которую наложено большее число связей в виде опорных стержней – рис. 1.1 а. Число «лишних» связей при внешней статической неопределимости определяется по формуле:
где Д – число жестких дисков, из которых состоит стержневая система; Ш – число простых шарниров, соединяющих между собой жесткие диски. Если шарнир соединяет более двух дисков, то он называется кратным и равен d-1 простым шарнирам(d – число соединяемых дисков); Со – число опорных стержней, наложенных на систему. Если стержневая система обладает замкнутыми контурами, а число наложенных связей обеспечивает только геометрическую неизменяемость (рис. 1.1 б), то такая система является внутренне статически неопределимой. Так как каждый замкнутый контур трижды статически неопределим, а шарнир в нем понижает неопределимость на единицу, то не сложно вывести формулу:
К – число замкнутых контуров;
Шк – число простых шарниров в замкнутых контурах. В случае, когда стержневая система и внешне и внутренне статически неопределима (рис. 1.1 в), то степень статической неопределимости устанавливают путем суммирования внешней и внутренней статической неопределимости:
Статически неопределимые стержневые системы обладают рядом преимуществ по сравнению с уже известными нам статически определимыми: 4. Большей жесткостью из-за наличия «лишних» связей. 4. Перераспределением внутренних усилий пропорционально жесткостям стержней. 4. Надежностью в эксплуатации, так как выход из работы связи не ведет к разрушению всей конструкции, а приводит к понижению ее статической неопределимости и перераспределением внутренних усилий. 4. Тепловое воздействие, осадка опор, неточность монтажа вызывают появление внутренних усилий. Это свойство требует учета перечисленных факторов воздействия в процессе проектирования, возведения и эксплуатации сооружений. Для расчета статически неопределимых систем разработаны два основных метода: метод сил и метод перемещений. В методе сил центральной задачей является определение усилий в «лишних» связях, а в методе перемещений – определение перемещений (угловых и линейных) всех узлов стержневой системы. На базе основных методов разработаны и другие – комбинированный и смешанный. Все перечисленные методы относятся к классическим и ориентированы в основном на ручной расчет, хотя с развитием вычислительной техники удалось в той или иной мере приспособить их к автоматизации расчетов. В настоящее время широко применяется метод конечных элементов (МКЭ) – метод, изначально разработанный для реализации на ЭВМ. На его базе разработаны ряд вычислительных комплексов – «Лира», «Мираж», «Скад» и др.. Сущность метода сил
Рассмотрим внешне статически неопределимую стержневую систему (рис. 1.2 а). Она обладает двумя «лишними связями, т.е. является дважды статически неопределимой:
Заменим «лишние связи неизвестными усилиями (рис. 1.2.б). Если неизвестные усилия Х1 и Х2 примут значения усилий опорных реакций HA и VA, то вторая схема станет эквивалентной первой, но при этом будет статически определимой. Назовем ее основной системой метода сил. Таким образом, для решения статически неопределимой рамы необходимо перейти к статически определимой, ей эквивалентной. Если найти каким-то образом усилия в «лишних» связях, то не будет уже сложным рассчитать статически определимую раму (основную систему метода сил) на действие заданной внешней нагрузки и известных уже усилий х1 и х2. Из сравнения заданной статически неопределимой рамы и выбранной основной системы (статически определимой) следует, что с кинематической точки зрения они будут эквивалентны лишь в случае, если перемещения по направлению отброшенных связей в основной системе будут равны перемещениям в заданной, т.е. равны нулю:
Определим перемещения D1 и D2:
В общем случае, когда отброшено к «лишних» связей:
где DiP – перемещение точки приложения силы хi по ее направлению от заданной нагрузки (умеем находить). Представим
dik – перемещение точки приложения силы хi по ее направлению от силы Тогда условие эквивалентности основной системы заданной статически неопределимой рамы можно записать так:
Физический смысл полученной системы уравнений – канонических уравнений метода сил в том, что перемещения по направлению отброшенных связей равны нулю. Из решения канонических уравнений метода сил и находятся искомые величины неизвестных усилий хi. После определения неизвестных усилий хi можно рассчитать основную систему как статически определимую, загруженную заданной нагрузкой и найденными усилиями хi.
Порядок расчета статически неопределимых рам методом сил. В силу того, что речь идет о ручном расчете статически неопределимых стержневых систем, то наряду с самим расчетом нам важна вторая сторона действия – контроль за расчетом. В связи с этим был выработан достаточно оптимальный алгоритм метода сил, а именно: 1. Определяем степень статической неопределимости (количество «лишних» связей): – внешне статически неопределимая система:
– внутренне статически неопределимая система:
– смешанная статическая неопределимость:
2. Выбираем основную систему метода сил (статически определимую, геометрически неизменяемую) путем замены «лишних» связей неизвестными усилиями xi. 3. Запишем систему канонических уравнений метода сил, отражающую условие равенства нулю перемещений по направлению отброшенных «лишних» связей (она в определенной мере подскажет ход последующих действий):
4. Найдем коэффициенты при неизвестных xi – dik и свободные члены DiP. Для этого основную систему последовательно загружаем единичными усилиями
5. Произведем проверку правильности определения коэффициентов dik и DiP. Для этого построим вспомогательную суммарную единичную эпюру изгибающих моментов –
Применяются следующие проверки: – универсальная: – построчная: – постолбцовая
6. Из решения системы канонических уравнений находим усилия xi. 7. Строим окончательную эпюру изгибающих моментов Мок путем наложения (сложения откорректированных эпюр
или 8. Проверим правильность построенной эпюры Мок. Для этого определим суммарное перемещение по направлению отброшенных связей в основной системе, которое должно равняться нулю – полная деформационная проверка:
а также в качестве проверки и для сужения области допущенной ошибки вычисляется перемещение по направлению конкретной i-й связи, которое также равно нулю:
9. Эпюру поперечных сил можно построить двумя способами: – традиционно, по участкам, с использованием метода сечений, рассматривая равновесие одной из отсеченных частей основной системы под действием внешней нагрузки и усилий xi; – используя построенную эпюру Мок и схемы загружения рассматриваемого стержня, в котором устанавливается поперечная сила, так как
где Мпр и Млев – соответственно правый и левый изгибающие моменты на концах стержня в эпюре Мок;
10. Эпюру нормальных сил также можно построить двумя способами: – традиционно, по участкам, с использованием метода сечений, рассматривая равновесие одной из отсеченных частей основной системы под действием внешней нагрузки и усилий xi (объединив с определением поперечных сил); – используя условие статического равновесия узлов под действием нормальных – неизвестных и поперечных, известных из эпюры Q, сил. После построения эпюр поперечных и нормальных сил проводим проверку результатов решения, используя для этого ранее не применявшиеся способы определения Q и N. |



 ,
, , где
, где
 .
.

 .
.
 ,
, – перемещение точки приложения силы xi по ее направлению от действительной силы xk, нам неизвестной;
– перемещение точки приложения силы xi по ее направлению от действительной силы xk, нам неизвестной; , где
, где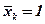 в основной системе, статически определимой, которое умеем находить).
в основной системе, статически определимой, которое умеем находить).
 , заданной внешней нагрузки и построим соответствующие эпюры изгибающих моментов
, заданной внешней нагрузки и построим соответствующие эпюры изгибающих моментов  и МР. Тогда
и МР. Тогда
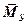 :
: или
или  .
. ;
; ;
; ;
; .
. с эпюрой МР):
с эпюрой МР): ,
, .
. ,
, .
.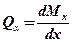 , то
, то ,
, – эпюра поперечных сил в рассматриваемом стержне от внешней нагрузки (чаще всего распределенной), когда стержень представлен балкой на двух шарнирных опорах;
– эпюра поперечных сил в рассматриваемом стержне от внешней нагрузки (чаще всего распределенной), когда стержень представлен балкой на двух шарнирных опорах; – длина рассматриваемого стержня.
– длина рассматриваемого стержня.