ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Связь момента силы относительно центра и относительно оси.

Лекция 6

Пространственная произвольная система сил - силы не лежат в одной плоскости и их линии действия не пересекаются в одной точке.

Для рассмотрения такой системы сил необходимо ввести новые понятия:

1. Момент силы относительно центра в пространстве.

2. Момент силы относительно оси.

3. Момент пары сил в пространстве.

Момент силы относительно центра в пространстве - векторная величина, равная векторному произведению радиуса-вектора, проведенного из центра к точке приложения силы, и вектора силы.

По определению векторного произведения вектор момента силы направлен перпендикулярно плоскости, проведенной через центр и силу, в ту сторону, откуда поворот радиуса-вектора к вектору силы виден против хода часовой стрелки на наименьший угол.

Модуль вектора момента силы относительно центра равен:

. Модуль вектора момента силы относительно центра численно равен удвоенной площади треугольника .

Момент силы относительно оси - алгебраическая величина, равная произведению проекции вектора силы на плоскость, перпендикулярную оси, на плечо этой проекции относительно точки пересечения оси с плоскостью, взятая со знаком + (плюс), если вращение плоскости под действием силы представляется при взгляде навстречу оси происходящим против часовой стрелки, и со знаком - (минус) в противном случае .

Момент силы относительно оси численно равен удвоенной площади треугольника .

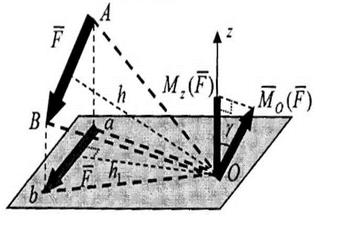
Связь момента силы относительно центра и относительно оси.

Модуль вектора момента силы относительно центра, лежащего на оси z, равен удвоенной площади треугольника ОАВ:

Момент силы относительно оси z, равен удвоенной площади треугольника : . Треугольник получен проекцией треугольника ОАВ на плоскость, перпендикулярную оси z, и его площадь связана с площадью треугольника ОАВ соотношением: , где - двугранный угол между плоскостями треугольников. Поскольку вектор момента силы относительно точки перпендикулярен плоскости треугольника ОАВ, то угол между вектором и осью равен углу . Таким образом, момент силы относительно оси есть проекция вектора момента силы относительно центра на эту ось:

Момент пары сил в пространстве - вектор, перпендикулярный плоскости действия пары, направленный в ту сторону, откуда вращение плоскости под действием пары представляется происходящим против часовой стрелки. Модуль вектора момента пары равен произведению одной из сил пары на плечо пары:

Теоремы о парах: (теоремы приводятся без доказательств)

О переносе пары сил в плоскость, параллельную плоскости ее действия - Пару сил можно перенести в любую плоскость, параллельную плоскости ее действия. Кинематическое состояние тела не изменится.

Об эквивалентности пар сил - Пару сил можно заменить другой парой сил, если их моменты геометрически (векторно) равны. Кинематическое состояние тела не изменится.

О сложении пар сил на плоскости - Систему пар сил на плоскости можно заменить одной парой, момент которой равен геометрической (векторной) сумме моментов исходных пар. Кинематическое состояние тела не изменится. Условие равновесия системы пар сил -

Далее будем по-прежнему придерживаться общего плана исследования системы сил, последовательно решая три вопроса:

1. Как упростить систему?

2. Каков простейший вид системы?

3. Каковы условия равновесия системы?

Приведение плоской произвольной системы сил к заданному центру - выбираем произвольную точку на плоскости и каждую из сил

переносим по методу Пуансо в эту точку.

Вместо исходной произвольной системы получим сходящуюся систему сил и систему пар.

В отличие от ранее рассмотренной плоской произвольной системы сил теперь при использовании метода Пуансо присоединенные пары сил характеризуются векторами.

Сходящиеся система сил приводится к одной силе, приложенной в центре приведения ( ).

Система пар приводится к одной паре, момент которой равен векторной сумме моментов исходных сил относительно центра приведения ( ).

В общем случае плоская произвольная система сил приводится к одной силе, называемой главным вектором и к паре с моментом, равным главному моменту всех сил системы относительно центра приведения:

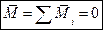
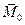, где - главный вектор; -главный момент.