 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Таза иілу кезіндегі кернеулер
Статика аксиомалары Статика бірнеше аксиомаға негізделеді. 1. Екі күш жүйесінің тепе-теңдігі туралы аксиома. Денеге түсетін екі күш тепе-теңдікте болу үшін олардың шамалары тең болуы және түсу нүктелері арқылы өтетін түзу бойымен қарама-қарсы бағытталуы қажетті де, жеткілікті де: F1 = F2, бірақ 2. Теңгерілген КЖ-н қосу және алып тастау аксиомасы. Күштер жүйесінің қатты денеге әсерін өзгертпей, соған теңгерілген КЖ-н қосуға немесе алып тастауға болады. Салдары: АҚД-ге түсетін күштің әсерін өзгертпей, оны әсер ету сызығы бойымен дененің кез келген басқа нүктесіне көшіруге болады (1.2 сурет), яғни күш -
3. Күштер параллелограмы аксиомасы. Өзара бұрыш құрып, бір нүктеге түсетін екі күштің тең әсерлісі сол күштер қабырғалары болып табылатын параллелограмның диагоналі ретінде анықталады (1.3 сурет), яғни 4. Өзара әрекеттену аксиомасы. Екі дене бір-біріне шамалары тең және бір түзу бойымен қарама-қарсы бағытталған күштермен әсер етеді: F21 = F12,
Еркін емес дене үшін келесі аксиома орын алады. 5. Байланыстар аксиомасы. Еркін емес денені, байланыстарды алып тастап және олардың әсерін реакциялармен ауыстырып, еркін дене ретінде қарастыруға болады. 6. Қатаю аксиомасы. Деформацияланатын дененің КЖ-нің әсерінен болған тепе-теңдік қалпы, оған қосымша байланыстарды орнатса, тіпті денені қатайған (абсолют қатты) дене ретінде қарастырса да, өзгермейді. Үш күш туралы теорема: егер дене бір жазықтықта орналасқан үш параллель емес күш әсерінен тепе-теңдік қалпында болса, онда сол күштердің әсер ету сызықтары бір нүктеде қиылысады. Дәлелдеу: Дене үш
2. Байланыстар және олардың р-ялары. Б-р аксиомасы. Б-ң нег. түрлері. Егер дененің кеңістікте кез келген орын ауыстыру алуға мүмкіншілігі болса, ол еркін дене деп аталады. Егер кейбір орын ауыстырулар мүмкін емес болса, дене еркін емес деп аталады. Дене қозғалысының еркіндігін шектейтін шарттар байланыстар деп аталады. Байланыстар қатты немесе икемді материялық денелер арқылы орындалады. Дене түскен күштер әсерінен байланыс кедергілік жасап тұрған орын ауыстыруды орындауға тырысып, оған күш түсіреді. Біржолы байланыс та денеге модулі тап сондай, бірақ қарама-қарсы бағытталған байланыстың реакциясы деп аталатын күшті түсіреді. Реакциялардан басқа күштерді актив (пәрменді) күштер деп атаймыз. Байланыс реакциясының актив күштерден айырмашылығы – оның шамасы актив күштерге тәуелді және алдын ала белгісіз. Реакцияның бағыты - байланыс дененің қозғалысына кедергілік жасайтын бағытқа қарама-қарсы. Кейбір байланыстардың (тіректердің) реакциялары қалай бағытталатынын қарастырайық: а) абсолют тегіс бет (үйкелісті ескермеуге болады) дененің бет үстінде жылжуына кедергілік жасамайды, ол тек қана бетке тік бағытпен қозғалуға кедергілік жасайды. Сондықтан оның реакциясы жанасып тұрған денелердің беттеріне ортақ нормаль бойымен бағытталады және жанасу нүктесіне түседі; б) икемді жіп немесе шынжыр. Мұнда реакция жіп в) цилиндрлік топса (подшипник) немесе жылжымайтын топсалы тұғыр. Тесіктерінен өтетін білікпен қосылған екі дене топсалы (шарнирлі) қосылысты құрайды. Біліктің өстік сызығы топсаның өсі деп аталады. Дене топса өсіне перпендикуляр бағытта орын ауыстыра алмайды, бірақ ол өске қатысты айнала алады. Сондықтан реакция топса өсіне перпендикуляр жазықтықта кез келген бағытталуы мүмкін. Әдетте оны екі құраушы күшке жіктейді; г) каток түріндегі тірек, яғни жылжымалы топсалы тұғыр. Үйкеліс күші ескерілмесе, реакция домалау бетінің нормалі бойымен бағытталады; д) сфералық топса және өкшелік. Мұндай байланыс дененің бір нүктесі ешқандай орын ауыстыру ала алмайтындай қылып бекітеді, ал сол нүктеге қатысты дене кеңістікте кез келген бағытта айналуы мүмкін. Реакция бекітілген нүкте арқылы өтеді; оның бағыты алдын ала белгісіз болғандықтан, оны үш құраушы күшке жіктейді; е) екі шетінде топсалармен бекітілген, салмағы ескерілмейтін сырық. Сырыққа топсалардың центрлерінде түсетін тек екі күш ғана әсер етеді. Сырық тепе-теңдікте болғандықтан, сол күштер (реакциялар) топсалардың центрлерінен өтетін түзу бойымен бағытталу керек.
Күштер жүйелері (КЖ) келесі түрлерге бөлінеді: тоғысатын КЖ, параллель күштер жүйесі, кез келген КЖ. Тоғысатын деп күштердің әсер ету сызықтары (ӘС) бір нүктеде қиылысатын КЖ-ні атайды. Параллель деп, ӘС өзара параллель КЖ-ні атайды. Кез келген деп ӘС қиылыспайтын және параллель емес КЖ-сі аталады. Аталған КЖ жазық және кеңістік болуы мүмкін. Егер барлық күштердің ӘС бір жазықтықта жатса, КЖ жазық деп, керісінше жағдайда кеңістік деп аталады. Дененің А, В, С, D нүктелерінде әсер ету сызықтары О нүктеде қиылысатын
Тоғысатын КЖ-нің тең әсерлі күшін аналитикалық тәсілмен анықталуын қарастырайық. Ол үшін (1.1) векторлық теңдеуінің декарт координат жүйесінің өстеріне проекцияларын жазып, тең әсерлі күшінің проекцияларын анықтаймыз
Тең әсерлі күшінің модулі келесі формуламен табылады
ал оның бағыты – үш бағыттаушы косинустар арқылы табылады
4. Тоғысатын күштер ж-ң векторлық, геометриялық, аналитикалық тепе теңдік шарттары. Тоғысатын КЖ тепе-теңдік қалпында
Тоғысатын жазық КЖ-нің тепе-теңдік шарттары мына түрде жазылады
5. Күштің нүктеге қатысты алгебралық және векторлық моменттері. Күштің өське қатысты алг. моменті.
мұндағы
күштер жүйесінің О нүктесіне қатысты бас моменті деп аталады. Жазық күштер жүйесі үшін күштің нүктеге қатысты векторлық моментінің орнына күштің нүктеге қатысты алгебралық моментін қолданған ыңғайлы, өйткені бұл жағдайда барлық күштердің векторлық моменттері бір- біріне параллель болады. Күштің нүктеге қатысты алгебралық моменті деп күш модулінің күш иініне көбейтіндісі аталады
Күш денені сағат тілінің қозғалысына қарсы бағытта айналдыруға тырысса алгебралық момент оң таңбамен, ал сағат тілінің қозғалысымен
Басқаша:
Күштің өске қатысты моменті, күш пен өс бір жазықтықта орналасса, нөлге тең. Күштің координат жүйесінің басына қатысты . Осыдан күштің координат өстеріне қатысты моменттерін табамыз
6. Күштер жұбы туралы түсінік. Күштер жұбының векторлық және алгебралық моменттері. Күштер жұптарының эвиваленттілігі туралы теорема. Күштер жұптарын қосу туралы т-ма. АҚД түсетін күштер жұбы деп модульдері өзара тең, параллель, бір біріне қарсы бағытталған және бір түзуде жатпайтын екі күштің жүйесін атаймыз (2.3 сурет). Жұп құрайтын күштердің векторлық қосындысы нөлге тең, бірақ күштер жұбы теңгерілмейді. Күштердің ӘС арасындағы ең қысқа қашықтық жұптың иіні d деп, ал күштер орналасқан жазықтық жұптың әсер ету жазықтығы деп аталады. Денеге түсетін бірнеше жұптардың жиынтығы күштер жұптарының жүйесі деп аталады. Жұп тең әсерлі күшке келтірілмейді. Жұптың денеге әсері, шамасы ±F∙d тең болатын M Күштер жұбының векторлық моменті Векторлық моменттері тең, бір жазықтықта немесе параллель жазықтықтарда орналасқан екі күштер жұбы, күш модульдері мен жұп иіндерінің шамаларына тәуелсіз, баламалы болады Егер күштер жұптары бір жазықтықта орналасса, олардың векторлық моменттері сол жазықтыққа перпендикуляр, денені айналдыруға тырысатын бағытына сәйкес бір немесе екінші жаққа бағытталады. Бұл жағдайда жұптардың моменттерін алгебралық шамалар ретінде қарастырып, моменттің модулі мен таңбасы арқылы айыруға болады. Жұп денені сағат тілінің қозғалысына қарсы айналдыруға тырысса, оның моменті оң, керісінше жағдайда теріс болып саналады. Сонда күштер жұптарының жазық жүйесі үшін және Жұптарды қосу туралы теорема: күштер жұптарының жүйесі векторлық моменті барлық жұптардың векторлық моменттерінің қосындысына тең бір ғана жұпқа баламалы, яғни
7. Күштерді параллель көшіру туралы теорема Күштер жүйесін берілген центрге келтіру туралы статианың негізгі теоремасы. (Пуансо) Қатты денеге түсетін күшті оның денеге әсерін өзгертпей, дененің кез келген басқа нүктесіне, күштер жұбын қосып, өзіне параллель көшіруге болады (2.4 сурет); жұптың моменті күштің сол нүктеге қатысты моментіне тең болуы тиіс.
АҚД-ге әсер ететін кез келген күштер жүйесін бір центрге келтіруге болады, сонда барлық күштер келтіру центріне түсетін жүйенің бас векторына тең бір күш пен моменті жүйенің сол центрге қатысты бас моментіне тең бір жұпқа ауыстырылады (2.5 сурет)
Мұнда АҚД-ге әсер ететін екі күштер жүйесі, олардың бас векторлары бірдей және кез келген нүктеге қатысты бас моменттері бірдей болғанда баламалы. Вариньон теоремасы: егер күштер жүйесінің тең әсерлі күші болса, оның кез келген нүктеге немесе өске қатысты моменті жүйенің барлық күштерінің сол нүктеге немесе өске қатысты моменттерінің қосындысына тең. 8. Кез-үштер жүйесінің тепе-теңдік шарттары Денеге әсер ететін кез келген күштер жүйесі оның
Бұл шарттар келесі тепе-теңдіктің аналитикалық шарттарына баламалы
яғни АҚД-ге әсер ететін кез келген күштер жүйесінің тепе-теңдігі үшін барлық күштердің декарт координат жүйесінің үш өсіне проекцияларының қосындылары және сол өстерге қатысты барлық күштердің моменттерінің қосындылары нөлге тең болуы қажетті де жеткілікті. Кеңістік параллель күштер жүйесі үшін (Oz өсі күштерге бағыттас) келесідей жазылады
9. кез келген жазық күштер жүйесінің тепе-теңдік шарттарының үш түрі. Жазық параллель күшт жүйесінің т-тк шарттары.Кез келген жазық күштер жүйесінің тепе-теңдік
Екінші түрі
мұнда Үшінші түрі
мұнда А, В, С бір түзудің бойында жатпау керек. Жазық параллель күштер жүйесі үшін тепе-теңдік шарттары келесідей
(мұнда Ox өсі күштерге перпендикуляр болмау керек) немесе
мұнда А мен В нүктелерінен өтетін түзу күштерге параллель болмау керек. 10.Сырғанау үйкелісі. Сырғанау үйкелісінің заңдары. Тегіс емес беттің реакциясы. Үйкеліс бұрышы. Сырғанау үйкелісінің Кулон – Амонтон заңдары: 1. Бір денені басқа дене үстінде ығыстыруға тырысқан жағдайда олардың жанасу жазықтығында 2. Максималды үйкеліс күші f үйкеліс коэффициенті мен N нормаль қысым күшінің көбейтіндісіне тең Fmax=f∙N. (3.10) Үйкеліс коэффициенті жанасатын денелердің материалдары мен беттерінің қалпына (кедір-бұдырлығына, температурасына, ылғалдылығына және т.б.) тәуелді өлшем бірліксіз шама, ол тәжірибе арқылы анықталады. f мәндері: ағаш пен ағаш арасында 0,4-0,7; металл мен металл - 0,15-0,25; болат пен мұз - 0,027. Тыныштық үйкелісі мен сырғанау үйкелісі айыра танылады. Тыныштық үйкелісінің коэффициенті тепе-теңдіктің шеткі қалпына, яғни сыртқы күштер кішкене ғана өскенде қозғалыс басталып кететін қалпына сәйкес келетін максималды Fmax үйкеліс күші арқылы анықталады. Әдетте ол сырғанау үйкелісінің коэффициентінен артық. Сырғанау жылдамдығының өсуімен сырғанау үйкелісінің коэффициенті басында шамалы азаяды, содан кейін айтарлықтай өзгермейді. 3. Максималды үйкеліс күші едәуір кең шектерде жанасатын беттердің ауданына тәуелсіз. Тегіс емес беттің реакциясы екі құраушы күштер арқылы есепке алынады: Егер дене горизонталь тегіс емес беттің үстінде болып, оған ауырлық күштен басқа ешқандай сыртқы күш түспесе, онда F = 0, ал толық реакция R = N және тіреуіш бетіне перпендикуляр болады. Денеге шамасы аз tg φ= Fmax/N=f . (3.11) Идеалды емес байланыстың толық реакциясының бағыты үйкеліс бұрышымен шеттеледі. Әдетте денелердің сырғанау үйкеліс күші ескерілуімен тепе-теңдіктің шеткі қалпы үшін үйкеліс күші максималды шамасына ие болғанда қарастырылады. Идеалды емес байланыстың реакциясы екі құраушымен көрсетіледі: N нормаль реакциясымен және Fmax максималды үйкеліс күшімен. 11. Қатты дененің ауырлық центрі. Дененің ауырлық центрінің координаттары. Ауырлық центрінің орнын анықтау тәсілдері: Дененің А1, A2 нүктелерінде түсетін екі параллель
Дене бөлшектеріне түсетін
С нүктесі
мұндағы 12 Нүкте қозғалысының берілу тәсілдерінүкте қозғалысы векторлық тәсілмен берілген жағдайда нүктенің жылдамдығы мен үдеуі. Нүктенің қозғалысы үш тәсілдердің біреуімен берілуі мүмкін. 1. Векторлық тәсіл. М нүктесі Oxyz санақ жүйесіне қатысты қозғалатын болсын. Нүктенің кез келген уақыт мезетіндегі орнын, оның
Бұл векторлық түрде жазылған нүктенің қозғалыс заңы. 2. Координаттық тәсіл. Нүктенің орнын оның уақыт өтуімен өзгеретін координаттарымен тікелей анықтауға болады
Бұл - тік бұрышты декарт координаттарындағы нүктенің қозғалыс заңы.
Нүкте қозғалысының негізгі кинематикалық сипаттамаларының біреуі жылдамдық болып келеді. t уақыт мезетінде
Нүктенің үдеуі - оның жылдамдығының модулі мен бағытының уақыт өтуімен өзгеруін сипаттайтын векторлық шама. Әлдебір t уақыт мезетінде нүктенің орны М және жылдамдығы
нүктенің берілген t уақыт мезетіндегі үдеуі деп аталады. Сонымен, нүктенің берілген уақыт мезетіндегі үдеу векторы жылдамдық векторының уақыт бойынша бірінші ретті туындысына, яғни 13. Қозғалыс координаттық тәсілімен берілген жағдайда нүктенің жылдамдығы мен үдеуі Келесі теореманы қолданамыз: вектордың туындысының қарастырылатын СЖ-нің қозғалмайтын өсіне проекциясы вектордың сол өске проекциясының туындысына тең. Сонда жылдамдықтың проекциялы үшін келесі орын алады
немесе Сонымен, жылдамдықтың координаттық өстерге проекциялары сәйкес координаттардың уақыт бойынша бірінші ретті туындыларына тең. Үдеудің проекциялары үшін келесі болады
немесе яғни үдеудің координаттық өстерге проекциялары жылдамдықтың сәйкес проекцияларының уақыт бойынша бірінші ретті туындыларына немесе кординаттардың екі ретті туындыларына тең. 4.5 Қозғалыс табиғи тәсілімен берілген жағдайда нүктенің жылдамдығы мен үдеуі Мұнда Нүктенің жылдамдығын анықтаймыз
Нүкте жылдамдығының траекториясына жанама өсіне проекциясы
Осыдан шығар Нүктенің үдеуі үшін
Мұнда
яғни үдеу векторы жанама және нормаль құраушыларының қосындысына тең
4.7 Қатты дененің тұрақты өс төңірегіндегі айналмалы қозғалысы АҚД-нің тұрақты (қозғалмайтын) өс төңірегінде айналғанда, оның өсте жатқан нүктелері қозғалмайды (4.5 суретіндегі АВ). Өс арқылы екі жазықтық жүргізейік – қозғалмайтын және денемен байланысып қозғалатын жазықтықты. Олардың арасындағы екі жақтық бұрышы дененің бұрылу бұрышы деп аталады, ол айналу өсінің оң бағыты жағынан қарағанда сағат тілінің қозғалысына қарсы болып көрінгенде, оң болып есептеледі. АҚД-нің тұрақты өс төңірегіндегі айналу заңы – келесі тәуелділік = (t). (4.16) Бұрыштық жылдамдық бұрышының уақыт өтуімен өзгеруін сипаттайды = d/dt, яғни Дененің бұрыштық жылдамдығын модулі || тең және айналу өсінің бойымен, ұшынан қарағанда дене сағат тілінің қозғалысына қарсы айналатын болып, бағытталған Бұрыштық үдеу бұрыштық жылдамдығының уақыт өтуімен өзгеруін сипаттайды = d/dt = d2 /dt2, яғни Егер қозғалыс кезінде =const болса, айналу бірқалыпты деп аталады. (4.17) формуласын интегралдап, айналу заңын анықтаймыз
Бірқалыпты айналу кезінде
Егер қозғалыс кезінде бұрыштық үдеу тұрақты болса(=const), айналу бірқалыпты айнымалы деп аталады, оның заңы келесі түрде жазылады
Егер мен таңбалары бірдей болса, айналу – бірқалыпты үдемелі, әртүрлі болса, бірқалыпты кемімелі болады. Айналатын дене нүктелерінің жылдамдықтары мен үдеулерін анықтаймыз (4.6 сурет). Айналу кезінде М нүктесі радиусы h тең, жазықтығы айналу өсіне перпендикуляр және P центрі өсте жататын шеңберді кескіндейді. dt уақыт ішінде дене dφ бұрышына бұрылады, М нүктесі ds = h∙ dφ орын ауыстыру жасайды. Сонда
Нүктенің үдеулерін анықтаймыз
бұрышы(4.6 сурет) келесі тәуелдік арқылы анықталады
Динамика аксиомалары Динамика деп материялық денелердің, олардың инерциясын есепке алуымен күштер әсерінен пайда болатын қозғалысын қарастыратын теориялық механиканың бөлімін атайды. Инерция деп материялық дененің өзінің қозғалыс немесе тыныштық қалпын күштер түспеген кезде сақтап қалу қасиетін айтады. Ілгерілемелі қозғалыстағы дененің инерциясының өлшемі болып табылатын зат мөлшеріне тәуелді физикалық шама дененің массасы m деп аталады. Нүкте динамикасы 4 аксиомаға негізделеді. 1-аксиома (инерция заңы): күштер түспейтін материялық нүкте (МН), оған күштер түсіп, қалпын өзгерткенге дейін тыныштықта немесе бірқалыпты түзу сызықты қозғалыста болады. Күштер болмағандағы нүктенің қозғалысы инерциялық қозғалыс деп аталады. Инерция заңы орындалатын санақ жүйесі (СЖ) инерциялық СЖ деп аталады. Көптеген есептерде Жермен байланысқан СЖ инерциялық деп алынады. 2-аксиома (динамиканың негізгі заңы): МН-нің үдеуі оған түсетін күшке пропорционал және сол күшпен бағыттас. Динамиканың негізгі теңдеуі
3-аксиома (әсер мен кері әсер заңы): екі МН бір-біріне модульдері тең және нүктелерді қосатын түзу бойымен қарама-қарсы бағытталған күштермен әсер етеді. 4-аксиома (күштер әсерінің тәуелсіздік заңы): әр күш бөлек түскенде МН алатын үдеулердің векторлық қосындысы барлық күштер біржолы түскенде алатын үдеуіне тең
(5.2) теңдеуінің орнына (5.1) теңдеуін, Ауырлық күш әсерінен денелер бірдей
Дененің массасы оның орналасуына және оған түсетін күштерге тәуелсіз, ал дененің салмағы дене орнының географикалық еніне және оның Жер орталығына дейінгі қашықтығына тәуелді еркін түсу үдеуінің өзгеруімен өзгеріп тұрады. 5.2 Материялық нүкте қозғалысының дифференциалдық теңдеулері МН { (5.2) теңдеуін декарт координат өстеріне проекциялап, декарт координаттарындағы қозғалысының дифференциалдық теңдеулерін (ҚДТ) аламыз
табиғи өстерге проекциялап, нүкте қозғалысының табиғи дифференциалдық теңдеулерін аламыз
ҚДТ нүкте динамикасының екі негізгі есебін шешу үшін қолданылады: 1-негізгі есеп: нүкте қозғалысы бойынша оған түсетін күшті анықтау. Мұнда МН қозғалысының теңдеулерін дифференциалдап, нәтижелерін (5.3) немесе (5.4) теңдеулеріне қою керек, содан нүктеге түсетін күш анықталады; 2-негізгі есеп: нүктеге түсетін күштер бойынша оның қозғалысын анықтау. Мұнда жалпы жағдайда (5.3) немесе (5.4) дифференциалдық теңдеулерінің екінші интегралдарын табу керек. Дербес жағдайларда ҚДТ айнамалыларды бөлу әдісінің көмегімен интегралдалуы мүмкін. 16. Материялық нүктенің салыстырмалы қозғалысы Динамика заңдары тек қана инерциалдық СЖ-нде орындалады. Материялық нүктенің кейбір СЖ-не қатысты қозғалысын қарастырайық және осы СЖ инерциалдық СЖ-не қатысты еркінше қозғалатын болсын. P нүктесі {
(5.5) теңдігін (5.4) теңдігіне қойып, түрлендіреміз
Келесі белгілерді қабылдаймыз
және
(5.6) теңдігін келесі түрде жазуға болады
(5.9) теңдеуі МН-нің салыстырмалы қозғалысы динамикасының негізгі теңдеуі деп аталады. МН-нің салыстырмалы қозғалысының теңдеулері абсолют қозғалысының теңдеулері секілді, түсетін күштерге тасымал және кориолис инерция күштерін қосып, құрастырылады. Қозғалатын инерциалдық емес СЖ-нің бақылаушы тасымал және кориолис инерция күштерін шынайы әсер ететін күштер секілді қабылдайды. Бірақ ол дұрыс емес, өйткені инерциалдық емес СЖ үшін механиканың Ньютон заңдары орындалмайды, сондықтан құбылыстарды алдыңғы аксиомалар қолдануымен қарастыруға болмайды. МН-нің салыстырмалы қозғалысы негізгі теңдеуінің дербес жағдайлары: а) ілгерілемелі тасымал қозғалыс кезінде |



 (1.1 сурет).
(1.1 сурет). жылжымалы вектор.
жылжымалы вектор.

 .
. .
. күштері әсерінен тепе-теңдікте дейік. Олар параллель емес және бір жазықтықта болғандықтан, екі
күштері әсерінен тепе-теңдікте дейік. Олар параллель емес және бір жазықтықта болғандықтан, екі  күштерінің әсер ету сызықтары қиылысады, сонда күштерді сол нүктеге көшіріп, тең әсерлі
күштерінің әсер ету сызықтары қиылысады, сонда күштерді сол нүктеге көшіріп, тең әсерлі  күшіне ауыстыруға болады. Енді
күшіне ауыстыруға болады. Енді  күші
күші  күшін теңгереді, сондықтан олардың әсер ету сызықтары түйіседі, яғни барлық үш күштердің әсер ету сызықтары бір нүктеде қиылысады.
күшін теңгереді, сондықтан олардың әсер ету сызықтары түйіседі, яғни барлық үш күштердің әсер ету сызықтары бір нүктеде қиылысады. немесе шынжыр бойымен бағытталады;
немесе шынжыр бойымен бағытталады; 3. Тоғысатын күштер жүйесі.
3. Тоғысатын күштер жүйесі. күштері түседі дейік (1.4,а сурет). Күштерді олардың ӘС бойымен О нүктеге көшіріп, оларды тізбектеп күштер үшбұрышы ережесімен қосамыз (1.4 б сурет). Алдымен
күштері түседі дейік (1.4,а сурет). Күштерді олардың ӘС бойымен О нүктеге көшіріп, оларды тізбектеп күштер үшбұрышы ережесімен қосамыз (1.4 б сурет). Алдымен  ,
,  күштерінің тең әсерлі
күштерінің тең әсерлі  күшін, сонан соң
күшін, сонан соң  ,
,  күштерінің тең әсерлі
күштерінің тең әсерлі  күшін, сөйтіп т.б. табамыз. Сонда:
күшін, сөйтіп т.б. табамыз. Сонда:  ,
,  ,
,  =
=  . Күштер саны n болса, онда
. Күштер саны n болса, онда  (1.1)
(1.1) векторын тұрғызып, оның ұшынан
векторын тұрғызып, оның ұшынан  векторын,
векторын,  содан кейін
содан кейін  ,
,  ,
,  . (1.2)
. (1.2) (1.3)
(1.3) ,
,  ,
,  . (1.4)
. (1.4) болуы үшін оның тең әсерлі күші нөлге тең болуы қажетті де, жеткілікті де, яғни
болуы үшін оның тең әсерлі күші нөлге тең болуы қажетті де, жеткілікті де, яғни  немесе
немесе  (тепе-теңдік шартының векторлық түрінде жазылуы). Тепе-теңдіктің геометриялық шарты – күш көпбұрышы тұйықталу керек, яғни соңғы күш векторының ұшы бірінші вектордың басымен түйісу керек. Тепе-теңдіктің аналитикалық шарттары - жүйедегі барлық күштердің үш координаттық өстеріне проекцияларының қосындылары нөлге тең болуы
(тепе-теңдік шартының векторлық түрінде жазылуы). Тепе-теңдіктің геометриялық шарты – күш көпбұрышы тұйықталу керек, яғни соңғы күш векторының ұшы бірінші вектордың басымен түйісу керек. Тепе-теңдіктің аналитикалық шарттары - жүйедегі барлық күштердің үш координаттық өстеріне проекцияларының қосындылары нөлге тең болуы ,
,  ,
,  . (1.5)
. (1.5) . (1.6)
. (1.6) күшінің О нүктесіне қатысты моменті деп О нүктесінде ОАВ үшбұрышының жазықтығына перпендикуляртүсетін және төмендегі формуламен анықталатын
күшінің О нүктесіне қатысты моменті деп О нүктесінде ОАВ үшбұрышының жазықтығына перпендикуляртүсетін және төмендегі формуламен анықталатын  векторы аталады (2.1 сурет)
векторы аталады (2.1 сурет) (2.1)
(2.1) - О нүктсінен
- О нүктсінен 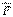 күші түсетін А нүктесіне жүргізілген радиус-вектор.
күші түсетін А нүктесіне жүргізілген радиус-вектор. векторының модулі күштің F модулі мен О нүктесінен күштің әсер ету сызығына дейін ең қысқа қашықтығының, яғни күштің О нүктеге қатысты иінінің көбейтіндісіне тең
векторының модулі күштің F модулі мен О нүктесінен күштің әсер ету сызығына дейін ең қысқа қашықтығының, яғни күштің О нүктеге қатысты иінінің көбейтіндісіне тең =F∙h. (2.2)
=F∙h. (2.2) моменті
моменті  радиус-векторы О нүктесінен тек қана А нүктесіне емес,
радиус-векторы О нүктесінен тек қана А нүктесіне емес,  күштер жүйесі үшін барлық күштердің О нүктесіне қатысты векторлық моменттерінің қосындысына тең вектор
күштер жүйесі үшін барлық күштердің О нүктесіне қатысты векторлық моменттерінің қосындысына тең вектор (2.3)
(2.3) . (2.4)
. (2.4) бағыттас айналдыруға тырысса теріс таңбамен алынады.
бағыттас айналдыруға тырысса теріс таңбамен алынады. . (2.5)
. (2.5)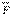 күшінің өске қатысты моменті деп күштің өске перпендикуляр жазықтыққа түсірілген проекциясының жазықтық пен өстің қиылысу нүктесіне қатысты алгебралық моменті аталады (2.2 сурет)
күшінің өске қатысты моменті деп күштің өске перпендикуляр жазықтыққа түсірілген проекциясының жазықтық пен өстің қиылысу нүктесіне қатысты алгебралық моменті аталады (2.2 сурет) . (2.6)
. (2.6) моменті (2.1) формуласына сай мына формуламен анықталады
моменті (2.1) формуласына сай мына формуламен анықталады
 ,
,  ,
,  . (2.7)
. (2.7) моментімен, жұптың әсер ету жазықтығының кеңістікте орналасуымен және жұптың денені айналдыруға тырысатын бағытымен сипатталады, сонда күштер жұбының моменті вектор болып табылады.
моментімен, жұптың әсер ету жазықтығының кеңістікте орналасуымен және жұптың денені айналдыруға тырысатын бағытымен сипатталады, сонда күштер жұбының моменті вектор болып табылады. – модулі жұп күшінің модулі мен жұп иінінің көбейтіндісіне тең вектор, оның бағыты жұптың әсер ету жазықтығына перпендикуляр және вектордың ұшынан қарағанда, жұп денені сағат тілінің қозғалысына қарсы айналдыруға тырысатын болып көрінеді. Күштер жұбын оның әсер ету жазықтығында және параллель жазықтыққа, күш модулі мен жұп иінін өзгертіп, бірақ жұп модулі мен оның денені айналдыруға тырысатын бағытын сақтап, көшіруге болады, яғни күштер жұбының векторлық моменті – еркін вектор.
– модулі жұп күшінің модулі мен жұп иінінің көбейтіндісіне тең вектор, оның бағыты жұптың әсер ету жазықтығына перпендикуляр және вектордың ұшынан қарағанда, жұп денені сағат тілінің қозғалысына қарсы айналдыруға тырысатын болып көрінеді. Күштер жұбын оның әсер ету жазықтығында және параллель жазықтыққа, күш модулі мен жұп иінін өзгертіп, бірақ жұп модулі мен оның денені айналдыруға тырысатын бағытын сақтап, көшіруге болады, яғни күштер жұбының векторлық моменті – еркін вектор. (2.8)
(2.8) . (2.9)
. (2.9) . Сонда қатты денеге әсер ететін күштер жұптары жүйесінің тепе-теңдік шарты келесідей жазылады
. Сонда қатты денеге әсер ететін күштер жұптары жүйесінің тепе-теңдік шарты келесідей жазылады . (2.10)
. (2.10) (2.11)
(2.11) . (2.12)
. (2.12)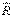 келтіру центрінің таңдалуына тәуелсіз, ал
келтіру центрінің таңдалуына тәуелсіз, ал  – тәуелді.
– тәуелді. бас векторына тең бір күшке және моменті жүйенің кез келген О центріне қатысты
бас векторына тең бір күшке және моменті жүйенің кез келген О центріне қатысты  бас моментіне тең күштер жұбына баламалы. Олай болса күштер жүйесі тепе-теңдікте болу үшін
бас моментіне тең күштер жұбына баламалы. Олай болса күштер жүйесі тепе-теңдікте болу үшін  , (3.1)
, (3.1) . (3.2)
. (3.2) ,
,  ,
, 


 , (3.3)
, (3.3) ,
,  . (3.4)
. (3.4) шарттарының бірінші түрі: күштердің екі координат өсіне проекцияларының қосындылары және кез келген центрге қатысты күштердің алгебралық моменттерінің қосындысы нөлге тең болуы қажетті де жеткілікті
шарттарының бірінші түрі: күштердің екі координат өсіне проекцияларының қосындылары және кез келген центрге қатысты күштердің алгебралық моменттерінің қосындысы нөлге тең болуы қажетті де жеткілікті ,
, 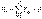 ,
,  . (3.5)
. (3.5) ,
,  ,
,  , (3.6)
, (3.6) түзуі
түзуі 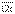 өсіне перпендикуляр емес болу керек.
өсіне перпендикуляр емес болу керек. ,
,  ,
,  (3.7)
(3.7)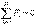 ,
,  (3.8)
(3.8) , (3.9)
, (3.9)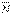 нормаль реакциясы (оның модулі нормаль қысым күшіне тең) және оған перпендикуляр
нормаль реакциясы (оның модулі нормаль қысым күшіне тең) және оған перпендикуляр  Толық реакция
Толық реакция  нормаль бағыттан α бұрышына ауытқиды (tg α = F/N).
нормаль бағыттан α бұрышына ауытқиды (tg α = F/N). үйкеліс күші пайда болады, және F≤ Fmax.
үйкеліс күші пайда болады, және F≤ Fmax.  вертикальдан үйкеліс бұрышы деп аталатын αmax бұрышына ауытқиды. Оны φ арқылы белгілеп, үйкеліс бұрышының тангенсі үйкеліс коэффициентіне тең екенін анықтаймыз
вертикальдан үйкеліс бұрышы деп аталатын αmax бұрышына ауытқиды. Оны φ арқылы белгілеп, үйкеліс бұрышының тангенсі үйкеліс коэффициентіне тең екенін анықтаймыз симметриялық пайдалану, қарапайым бөліктерге жіктеу, теріс массалар тәсілі.
симметриялық пайдалану, қарапайым бөліктерге жіктеу, теріс массалар тәсілі. және
және  күштерін қарастырайық (3.5 сурет).
күштерін қарастырайық (3.5 сурет).  тең әсерлі күшінің әсер ету сызығы қосылатын күштерге параллель және A1A2 түзуінде жатқан С нүктесінен өтеді. С нүктесінің орнын Вариньон теоремасын қолданып анықтай аламыз:
тең әсерлі күшінің әсер ету сызығы қосылатын күштерге параллель және A1A2 түзуінде жатқан С нүктесінен өтеді. С нүктесінің орнын Вариньон теоремасын қолданып анықтай аламыз:  , осыдан
, осыдан . (3.13)
. (3.13) ,
,  күштерін А1, А2 нүктелерінің айналасында бірдей α бұрышына бұрғанда, тең әсерлі күші де сол бағытта α бұрышына бұрылады және дәл сол С нүктесіне түседі. С нүктесі
күштерін А1, А2 нүктелерінің айналасында бірдей α бұрышына бұрғанда, тең әсерлі күші де сол бағытта α бұрышына бұрылады және дәл сол С нүктесіне түседі. С нүктесі  параллель күштердің центрі деп аталады. Кез келген күштер саны үшін де осылай болады.
параллель күштердің центрі деп аталады. Кез келген күштер саны үшін де осылай болады. ,
,  ,…,
,…,  ауырлық күштерінің тең әсерлісін
ауырлық күштерінің тең әсерлісін  деп белгілейік (3.6 сурет). Осы күштің модулі дененің салмағы деп аталады және келесі теңдікпен анықталады
деп белгілейік (3.6 сурет). Осы күштің модулі дененің салмағы деп аталады және келесі теңдікпен анықталады . (3.14)
. (3.14)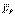 параллель ауырлық күштерінің центрі болып келеді, ол дененің ауырлық центрі деп аталады. Сонымен, АҚД-нің ауырлық центрі – денемен өзгеріссіз байланысқан дененің кеңістікте кез келген орналасуында дене бөлшектеріне түсетін ауырлық күштерінің тең әсерлі күшінің әсер ету сызығы өтетін нүкте. Ауырлық центрінің координаттары келесі формулалармен анықталады
параллель ауырлық күштерінің центрі болып келеді, ол дененің ауырлық центрі деп аталады. Сонымен, АҚД-нің ауырлық центрі – денемен өзгеріссіз байланысқан дененің кеңістікте кез келген орналасуында дене бөлшектеріне түсетін ауырлық күштерінің тең әсерлі күшінің әсер ету сызығы өтетін нүкте. Ауырлық центрінің координаттары келесі формулалармен анықталады ,
,  ,
,  (3.15)
(3.15) ,
,  ,
,  – ауырлық
– ауырлық  күштері түсетін нүктелердің координаттары.
күштері түсетін нүктелердің координаттары. радиус-векторының (4.1 сурет) t уақытына тәуелдігін беріп, анықтауға болады.
радиус-векторының (4.1 сурет) t уақытына тәуелдігін беріп, анықтауға болады. . (4.1)
. (4.1) . (4.2)
. (4.2)
 3. Табиғи тәсіл. Нүкте қозғалысын табиғи тәсілмен беру – бұл оның траекториясын (4.2 сурет), траекториясындағы санақ басы мен санақ бағытын және қозғалыс заңын келесі түрде беру
3. Табиғи тәсіл. Нүкте қозғалысын табиғи тәсілмен беру – бұл оның траекториясын (4.2 сурет), траекториясындағы санақ басы мен санақ бағытын және қозғалыс заңын келесі түрде беру . (4.3)
. (4.3) радиус-векторымен анықталатын М орнында, ал t1 уақыт мезетінде
радиус-векторымен анықталатын М орнында, ал t1 уақыт мезетінде 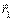 радиус-векторымен анықталатын М1 орнында болсын дейік (4.3 сурет). Сонда
радиус-векторымен анықталатын М1 орнында болсын дейік (4.3 сурет). Сонда 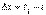 уақыт аралығында нүктенің орын ауыстыруы
уақыт аралығында нүктенің орын ауыстыруы  орын ауыстыру векторымен анықталады. ОММ1 үшбұрышынан
орын ауыстыру векторымен анықталады. ОММ1 үшбұрышынан  болатыны көрінеді, яғни
болатыны көрінеді, яғни  . Орын ауыстыру векторының сәйкес уақыт аралығына қатынасы, нүктенің t уақыт аралығындағы модулі мен бағыты бойынша ортақ жылдамдығы деп аталатын векторлық шамасын береді,
. Орын ауыстыру векторының сәйкес уақыт аралығына қатынасы, нүктенің t уақыт аралығындағы модулі мен бағыты бойынша ортақ жылдамдығы деп аталатын векторлық шамасын береді,  .
. векторлық шамасы нүктенің t уақыт мезетіндегі жылдамдығы деп аталады, сонда нүктенің жылдамдығы
векторлық шамасы нүктенің t уақыт мезетіндегі жылдамдығы деп аталады, сонда нүктенің жылдамдығы  векторының t аргументі бойынша бірінші ретті туындысы болып келеді
векторының t аргументі бойынша бірінші ретті туындысы болып келеді . (4.4)
. (4.4) болсын, ал t1 мезетінде нүкте M1 орнына келіп,
болсын, ал t1 мезетінде нүкте M1 орнына келіп,  жылдамдығына ие болады дейік (4.4 сурет). Сонда
жылдамдығына ие болады дейік (4.4 сурет). Сонда  уақыт аралығында нүктенің жылдамдығы
уақыт аралығында нүктенің жылдамдығы  өсімін алады, ол әрқашан траекториясының ойыс жағына бағытталады.
өсімін алады, ол әрқашан траекториясының ойыс жағына бағытталады.  векторының t аралығына қатынасы нүктенің сол ауқыт аралығындағы орташа үдеуін анықтайды. t нөлге ұмтылған кезде
векторының t аралығына қатынасы нүктенің сол ауқыт аралығындағы орташа үдеуін анықтайды. t нөлге ұмтылған кезде  ұмтылатын векторлық шама
ұмтылатын векторлық шама (4.5)
(4.5) нүктенің радиус-векторының екінші ретті туындысына тең.
нүктенің радиус-векторының екінші ретті туындысына тең.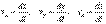 (4.6)
(4.6) . (4.7)
. (4.7) ,
,  ,
,  (4.8)
(4.8) , (4.9)
, (4.9) мен
мен  векторларын олардың Мnb табиғи үшжақтықтың М нүктесінен басталып, сонымен бірге қозғалатын өстеріне проекциялары арқылы табылады. Өстердің бағыттары: М - s санағының оң бағытына сәйкес траекторияға жанама бойынша; Мn бас нормалі – траекториямен жанасу жазықтығында траекторияның ойыс жағына жүргізілген нормалі бойынша; Mb бинормалі – алдынғы екі өске перпендикуляр бойынша олармен оң өстер жүйесін құрайтын болып бағытталады.
векторларын олардың Мnb табиғи үшжақтықтың М нүктесінен басталып, сонымен бірге қозғалатын өстеріне проекциялары арқылы табылады. Өстердің бағыттары: М - s санағының оң бағытына сәйкес траекторияға жанама бойынша; Мn бас нормалі – траекториямен жанасу жазықтығында траекторияның ойыс жағына жүргізілген нормалі бойынша; Mb бинормалі – алдынғы екі өске перпендикуляр бойынша олармен оң өстер жүйесін құрайтын болып бағытталады. . (4.10)
. (4.10) . (4.11)
. (4.11) және жылдамдықтың модулі
және жылдамдықтың модулі  .
. (4.12)
(4.12) (ρ – қарастырылатын орнында нүктенің траекториясының қисықтық радиусы), сонда
(ρ – қарастырылатын орнында нүктенің траекториясының қисықтық радиусы), сонда , (4.13)
, (4.13) . (4.14)
. (4.14) векторы жанасу жазықтығында жатады, яғни Mn жазықтығында. (4.13) теңдігінің екі жағын М, Мn және Mb өстеріне проекциялап, келесіге келеміз
векторы жанасу жазықтығында жатады, яғни Mn жазықтығында. (4.13) теңдігінің екі жағын М, Мn және Mb өстеріне проекциялап, келесіге келеміз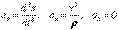 . (4.15)
. (4.15) . (4.17)
. (4.17)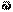 векторымен кескіндеуге болады.
векторымен кескіндеуге болады. . (4.18)
. (4.18) (4.19)
(4.19) болса, онда
болса, онда . (4.19’)
. (4.19’) . (4.20)
. (4.20)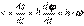 . (4.21)
. (4.21) (4.22)
(4.22) үдеуі траекторияға жанама бағытталады (үдемелі айналу кезінде айналу бағытына сәйкес және кемімелі айналу кезінде айналу бағытына қарсы),
үдеуі траекторияға жанама бағытталады (үдемелі айналу кезінде айналу бағытына сәйкес және кемімелі айналу кезінде айналу бағытына қарсы),  үдеуі әрқашан МP радиусы бойымен өске қарай бағытталады. Нүктенің толық үдеуі
үдеуі әрқашан МP радиусы бойымен өске қарай бағытталады. Нүктенің толық үдеуі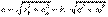 (4.23)
(4.23) . (4.24)
. (4.24) және
және 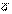 векторлары үшін келесі формулуларды шығаруға болады
векторлары үшін келесі формулуларды шығаруға болады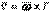 , (4.25)
, (4.25) (4.26)
(4.26) . (5.1)
. (5.1) (5.2)
(5.2) күші ретінде тең әсерлі күшті алып, қолдануға болады.
күші ретінде тең әсерлі күшті алып, қолдануға болады. үдеуіне ие болады, ол ауырлық күш үдеуі немесе еркін түсу үдеуі деп аталады. Егер МН-ге тек қана
үдеуіне ие болады, ол ауырлық күш үдеуі немесе еркін түсу үдеуі деп аталады. Егер МН-ге тек қана  ауырлық күші түсетін болса, онда (5.1) бойынша
ауырлық күші түсетін болса, онда (5.1) бойынша . (5.2)
. (5.2) } күштер жүйесінің әсерінен инерциалдық Оxyz санақ жүйесіне қатысты қозғалатын болсын, және күштер арасына байланыстардың реакциялары да кіреді деп есептейміз.
} күштер жүйесінің әсерінен инерциалдық Оxyz санақ жүйесіне қатысты қозғалатын болсын, және күштер арасына байланыстардың реакциялары да кіреді деп есептейміз.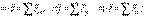 (5.3)
(5.3) (5.4)
(5.4) } күштер әсерінен қозғалатын болсын. Инерциалдық СЖ-нде динамиканың негізгі (5.2) теңдеуі орындалады. Нүктенің абсолют үдеуі (5.17) формуласымен табылады
} күштер әсерінен қозғалатын болсын. Инерциалдық СЖ-нде динамиканың негізгі (5.2) теңдеуі орындалады. Нүктенің абсолют үдеуі (5.17) формуласымен табылады (5.5)
(5.5) (5.6)
(5.6) (5.7)
(5.7) (5.8)
(5.8) және
және  векторлары сәйкес тасымал және кориолис инерция күштері деп аталады.
векторлары сәйкес тасымал және кориолис инерция күштері деп аталады. (5.9)
(5.9)
