 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Улучшение базисного решения ТЗЛП. Циклы пересчета
Постановка транспортной задачи линейного программирования Определение 12.1. Транспортной задачей линейного программирования (ТЗЛП) называется задача, в которой необходимо найти оптимальный план перевозок груза от отправителей к получателям, минимизировав при этом суммарную стоимость перевозок этого груза. Пусть имеется Обозначим через
Условия (12.1) определяют полный вывоз продукции от всех поставщиков. Условия (12.2) означают полное удовлетворение спроса во всех пунктах потребления. Условия (12.1) – (12.2) представляют собой систему Транспортная задача (12.1) – (12.3) может быть решена обычным симплекс-методом, но в силу ее особенностей для нее разработан специальный метод решения, основанный на ряде основных теорем. Заметим, что ранг матрицы системы (12.1) – (12.2) на единицу меньше числа уравнений: Теорема 12.1.Для разрешимости транспортной задачи (12.1) – (12.3) необходимо и достаточно выполнение равенства (условия баланса)
Определение 12.2.Транспортную задачу, в которой выполняется равенство (12.4), называют закрытой (сбалансированной). Транспортную задачу, в которой не выполняется равенство (12.4), называют открытой. Согласно теореме 12.1, любая закрытая ТЗЛП имеет оптимальное решение. Решение открытой ТЗЛП можно свести к решению закрытой ТЗЛП. Условия ТЗЛП (12.1) – (12.3) записываются в так называемой транспортной таблице (см. табл. 12.1). Таблица 12.1.
Для дальнейшего рассмотрения теории нам понадобится задача, двойственная к ТЗЛП (12.1) – (12.3). Обозначим переменные двойственной задачи, соответствующие уравнениям (12.1), через Определение 12.3.Переменные Потенциалы отправителей и получателей, как двойственные оценки ресурсов (запасов и потребностей) ТЗЛП можно интерпретировать как цены продукта в соответствующих пунктах отправителей и получателей. Тогда задача, двойственная к ТЗЛП (12.1) – (12.3), примет вид
Отметим, что пара задач (12.1) – (12.3) и (12.5) – (12.6) является несимметрической парой ЗЛП. Поэтому переменные Так как закрытая ТЗЛП всегда имеет оптимальное решение – матрицу Из второй теоремы теории двойственности следует, что любое допустимое решение
Отметим, что в силу равенств (12.1), (12.2) условия (12.7) выполняются при любых значениях потенциалов
Итерационный процесс поиска решения закрытой ТЗЛП (оптимального плана перевозок) начинают с построения некоторого базисного (опорного) допустимого плана. Для составления первого базисного плана перевозок существует несколько приемов (метод наименьших стоимостей, метод северо-западного угла, метод минимального элемента). Наиболее рациональным из них является метод наименьших стоимостей, который позволяет построить первоначальный базисный план перевозок, являющийся наиболее близким к оптимальному. Основой построения первоначального базисного плана является то свойство ТЗЛП, что любой базисный план задает положительные значения для Клетки таблицы будем обозначать через Рассмотрим алгоритм метода наименьших стоимостей. При построении первого базисного решения первыми заполнить клетки с наименьшей стоимостью перевозок Определение 13.1.В транспортной таблице поставок занятые клетки называются базисными, незанятые – свободными. Определение 13.2. Клетку с нулевой поставкой называют условно занятой (формально занятой). Определение 13.3.Если в транспортной таблице число Замечание 13.1.Для дальнейшего решения закрытой ТЗЛП методом потенциалов необходимо, чтобы базисный допустимый план являлся невырожденным. Если же базисный план является вырожденным, то его преобразовать в невырожденный, используя следующие рекомендации: 1) если 2) если Пример 13.1.Составить первоначальный базисный план ТЗЛП, если запасы отправителей представлены вектором запасов
Решение.Согласно алгоритму метода наименьшей стоимости, заполнение начинаем с клетки, имеющей наименьшую стоимость В клетку В клетку Итак, первоначальный базисный план представлен в табл. 13.1. Таблица 13.1.
Выпишем по табл. 13.1 матрицу транспортных перевозок
Проверим составленный план на невырожденность. В нашем случае Чтобы базисный план стал невырожденным, необходимо одну свободную клетку превратить в формально занятую клетку. В клетку Значение целевой функции на базисном решении (суммарная стоимость перевозок груза) равна
Предположим, что для закрытой ТЗЛП составлен невырожденный первоначальный базисный план. Переменные, соответствующие занятым (базисным) клеткам транспортной таблицы обозначим через Согласно §12, для того, чтобы базисный план 1) для базисных переменных
2) для свободных переменных
Числа Следующая теорема непосредственно вытекает из проведенных выше рассуждений. Теорема 14.1 (теорема о потенциалах). Пусть для закрытой ТЗЛП (12.1) – (12.3) составлен невырожденный базисный план Сформулируем алгоритм решения ТЗЛП (12.1) – (12.3). 1) Составить невырожденный первоначальный базисный план (начальный план перевозок) методом наименьшей стоимости. 2) Поставить в соответствие 3) Решить составленную в пункте 2) систему для потенциалов. При этом следует иметь в виду, что эта система совместна, и число неизвестных в ней на одну больше, чем число уравнений ( 4) Подставляя найденные в пункте 3) значения потенциалов
Если условия (14.2) выполняются для всех свободных клеток, то базисное решение является оптимальным. Задача решена. Заметим, что в этом случае
то базисный план не является оптимальным, и необходимо улучшить базисное решение путем перевода одной свободной клетки в разряд занятых. Процесс улучшения повторяется до тех пор, пока не будет получено базисное решение, для которого выполняются оба условия (14.1) – (14.2). Замечание 14.1. При решении ТЗЛП методом потенциалов рекомендуется составить так называемую матрицу оценок
Тогда, если для составленного базисного плана ТЗЛП (12.1) – (12.3) все элементы матрицы оценок Пример 14.1. Проверить на оптимальность базисный план ТЗЛП, представленный в табл. 14.1, пользуясь методом потенциалов. В случае оптимальности найти минимум суммарных издержек на перевозку груза. Таблица 14.1.
Выпишем по табл. 14.1 матрицу транспортных перевозок
Базисный план является невырожденным, так как Поставим в соответствие
относительно неизвестных потенциалов
Найдем для свободных клеток оценочные коэффициенты свободная клетка свободная клетка свободная клетка свободная клетка свободная клетка свободная клетка Составим матрицу оценок
Так как в матрице оценок
Улучшение базисного решения ТЗЛП. Циклы пересчета Пусть составленный невырожденный план закрытой ТЗЛП (12.1) – (12.3) не является оптимальным, то есть для некоторых свободных клеток условие (14.2) не выполняется. Выпишем оценочные коэффициенты
Неоптимальность базисного плана ТЗЛП (12.1) – (12.3) означает, что среди оценочных коэффициентов Выберем какую-нибудь из свободных переменных Определение 15.1.Циклом пересчета, соответствующим данной свободной клетке 1) ее звенья параллельны строкам и столбцам таблицы (направление отдельных отрезков контура может быть только горизонтальным и вертикальным); 2) в каждой вершине ломаной под прямым углом сходятся два ее звена. При этом нельзя рассматривать в качестве вершин клетки, в которых отрезки пересекаются; 3) число вершин ломаной должно быть четным. Можно доказать, что при выполнении трех условий для любой свободной клетки транспортной таблицы существует только один цикл пересчета. Этот цикл может быть представлен в простейшем случае как прямоугольником (квадратом), так и самопересекающейся ломаной (точки пересечения отрезков ломаной не являются вершинами цикла). Построим цикл пересчета, соответствующий свободной клетке
Первоначально в клетке После того, как цикл пересчета определен и знаки в нем расставлены, необходимо изменить поставки в вершинах цикла в соответствии со знаками на величину
Величина 1) ни одна из поставок в клетке со знаком “–” не стала отрицательной; 2) поставка Чтобы величина Можно показать, что цикл пересчета позволяет уменьшить значение целевой функции (12.3) ТЗЛП на величину В результате процесса улучшения базисного плана получится новый базисный план, который снова проверяется на оптимальность при помощи метода потенциалов. Из общих свойств задач линейного программирования следует, что через конечное число итераций (построения циклов пересчета) будет получен оптимальный план. Пример 15.1. Решить методом потенциалов ТЗЛП, если запасы отправителей представлены вектором запасов
Решение. Транспортная задача является закрытой: Первоначальный базисный план, составленный по методу наименьшей стоимости, представлен в табл. 15.1. Таблица 15.1.
Значение целевой функции на этом плане равно
Базисный план является невырожденным, так как Поставим в соответствие
относительно неизвестных потенциалов
Непосредственно убеждаемся, что для свободной клетки
(для других свободных клеток Цикл пересчета (см. табл. 15.1) имеет вид:
в котором
Рис. 15.1. Используя клетки со знаком “–”, находим поставку Таблица 15.2.
Значение целевой функции на этом плане равно
то есть в результате первой итерации (цикла пересчета) значение целевой функции уменьшили на Проверим базисный план, составленный в табл. 15.2., на оптимальность методом потенциалов. Решая систему
относительно потенциалов
Непосредственно убеждаемся, что теперь для свободной клетки оценочный коэффициент
(для других свободных клеток
в котором
Рис. 15.2. Используя свободные клетки со знаком “–”, находим поставку Таблица 15.3.
©2015 www.megapredmet.ru Все права принадлежат авторам размещенных материалов. |



 отправителей (поставщиков)
отправителей (поставщиков)  , у которых сосредоточено количество
, у которых сосредоточено количество  ,
, 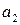 , …,
, …,  единиц однородного продукта. Данный продукт потребляется в
единиц однородного продукта. Данный продукт потребляется в  пунктах
пунктах  ,
, 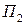 , …,
, …,  (назовем их потребителями). Объемы потребления
(назовем их потребителями). Объемы потребления  ,
, 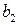 , …,
, …,  единиц. Расходы на перевозку единицы продукта из пункта
единиц. Расходы на перевозку единицы продукта из пункта  в пункт
в пункт  оцениваются величиной
оцениваются величиной 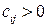 и приводятся в матрице транспортных расходов
и приводятся в матрице транспортных расходов  . Требуется составить такой план прикрепления потребителей к поставщикам (план перевозок, план поставок), при котором часть продукта вывозится из пункта
. Требуется составить такой план прикрепления потребителей к поставщикам (план перевозок, план поставок), при котором часть продукта вывозится из пункта  (
(  ,
,  ) количество продукта, перевозимого из пункта
) количество продукта, перевозимого из пункта  обозначим матрицей
обозначим матрицей  (ее называют матрицей транспортных перевозок). Тогда математическая модель ТЗЛП имеет вид
(ее называют матрицей транспортных перевозок). Тогда математическая модель ТЗЛП имеет вид (
(  (
(  , (12.3)
, (12.3) линейных алгебраических уравнений с
линейных алгебраических уравнений с  неизвестными
неизвестными  (
(  линейно независимых уравнений, то есть любое базисное (опорное) решение должно содержать
линейно независимых уравнений, то есть любое базисное (опорное) решение должно содержать 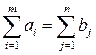 . (12.4)
. (12.4)
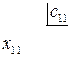
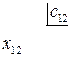









 (
(  (
(  (
(  . (12.6)
. (12.6) (
(  транспортных перевозок, то согласно первой теореме теории двойственности, соответствующая двойственная задача (12.5) – (12.6) также имеет оптимальное решение.
транспортных перевозок, то согласно первой теореме теории двойственности, соответствующая двойственная задача (12.5) – (12.6) также имеет оптимальное решение. ТЗЛП (12.1) – (12.3) и допустимое решение
ТЗЛП (12.1) – (12.3) и допустимое решение  (
(  (
(  (
( 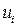 ,
,  . Поэтому существенными для потенциалов
. Поэтому существенными для потенциалов  .
. . При заполнении очередной (не последней) клетки
. При заполнении очередной (не последней) клетки  необходимо присваивать соответствующей переменной
необходимо присваивать соответствующей переменной  базисных клеток равно
базисных клеток равно  , то соответствующий план перевозок называют невырожденным. Если в транспортной таблице число
, то соответствующий план перевозок называют невырожденным. Если в транспортной таблице число  , то необходимо
, то необходимо  свободных клеток превратить в формально занятые (в соответствующие клетки назначить поставку
свободных клеток превратить в формально занятые (в соответствующие клетки назначить поставку  );
); , то необходимо
, то необходимо  занятых клеток превратить в свободные клетки. Сделать это можно при помощи циклов перерасчета (см. §15).
занятых клеток превратить в свободные клетки. Сделать это можно при помощи циклов перерасчета (см. §15).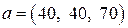 , потребности получателей – вектором потребностей
, потребности получателей – вектором потребностей 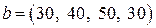 . Матрица транспортных расходов
. Матрица транспортных расходов .
. . В клетку
. В клетку  помещаем поставку в объеме
помещаем поставку в объеме  , в результате чего исключается получатель
, в результате чего исключается получатель  , имеющей стоимость
, имеющей стоимость  , помещаем поставку в объеме
, помещаем поставку в объеме  , в результате чего исключаем получателя
, в результате чего исключаем получателя  , имеющей стоимость
, имеющей стоимость 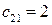 , поместить нулевую поставку
, поместить нулевую поставку  , то мы исключим отправителя
, то мы исключим отправителя  , имеющей стоимость
, имеющей стоимость  , помещаем поставку в объеме
, помещаем поставку в объеме  , в результате чего исключаем получателя
, в результате чего исключаем получателя  . Итак, клетки со стоимостью, равной 1, оказались все занятыми.
. Итак, клетки со стоимостью, равной 1, оказались все занятыми. , имеющей стоимость
, имеющей стоимость  , помещаем поставку
, помещаем поставку  , в результате чего будет исключен отправитель
, в результате чего будет исключен отправитель  , имеющей стоимость
, имеющей стоимость  , помещаем поставку
, помещаем поставку  , в результате чего будет исключен отправитель
, в результате чего будет исключен отправитель  .
.










 .
. ,
,  , количество занятых клеток равно
, количество занятых клеток равно  . Так как
. Так как  .
. . Причем, если базисный план является невырожденным, то все
. Причем, если базисный план является невырожденным, то все  .
. , и поэтому из (12.8) следует, что потенциалы
, и поэтому из (12.8) следует, что потенциалы  ; (14.1)
; (14.1) . (14.2)
. (14.2) ,
,  обозначают стоимости перевозки груза от отправителя к получателю для базисных и свободных клеток транспортной задачи.
обозначают стоимости перевозки груза от отправителя к получателю для базисных и свободных клеток транспортной задачи.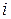 -му уравнению системы (12.1) потенциал
-му уравнению системы (12.1) потенциал 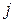 -ому уравнению системы (12.2) потенциал
-ому уравнению системы (12.2) потенциал 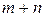 неизвестными потенциалами.
неизвестными потенциалами.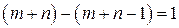 ). Поэтому, одну из неизвестных (любую) можно взять произвольно (например, обнулить), и найти остальные неизвестные.
). Поэтому, одну из неизвестных (любую) можно взять произвольно (например, обнулить), и найти остальные неизвестные. ,
,  .
.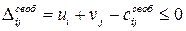 . Если для некоторых свободных переменных
. Если для некоторых свободных переменных  :
: ,
,  ,
, , где элементы
, где элементы  этой матрицы удовлетворяют условию:
этой матрицы удовлетворяют условию: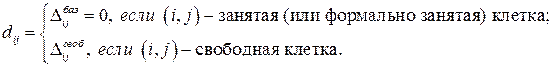
 неположительны, то этот план является оптимальным планом. Если же в матрице оценок
неположительны, то этот план является оптимальным планом. Если же в матрице оценок  , то этот базисный план не является оптимальным и подлежит улучшению.
, то этот базисный план не является оптимальным и подлежит улучшению.











 .
.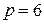 (
(  ).
). ), а
), а  ). Составим для занятых (базисных) клеток систему
). Составим для занятых (базисных) клеток систему
 (он чаще всего встречается в системе) и найдем значения остальных потенциалов:
(он чаще всего встречается в системе) и найдем значения остальных потенциалов:
 :
: :
: 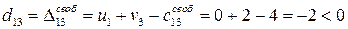 ,
, :
: 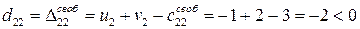 ,
, :
:  ,
, :
:  ,
, :
:  ,
, :
:  .
. .
. транспортных перевозок) является оптимальным. Вычислим минимум суммарных издержек на перевозку груза:
транспортных перевозок) является оптимальным. Вычислим минимум суммарных издержек на перевозку груза: .
. (обычно выбирается такая переменная, для которой оценочный коэффициент наибольший). Пусть для определенности выбрана свободная переменная
(обычно выбирается такая переменная, для которой оценочный коэффициент наибольший). Пусть для определенности выбрана свободная переменная  , соответствующая свободной клетке
, соответствующая свободной клетке  . Необходимо перевести эту свободную переменную в разряд занятых, а соответствующую старую базисную переменную – в разряд свободных. Для решения этой подзадачи используются так называемые циклы пересчета, позволяющие улучшить базисный план (уменьшить значение целевой функции).
. Необходимо перевести эту свободную переменную в разряд занятых, а соответствующую старую базисную переменную – в разряд свободных. Для решения этой подзадачи используются так называемые циклы пересчета, позволяющие улучшить базисный план (уменьшить значение целевой функции).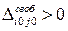 . Пусть последовательность вершин, образующих данный цикл, имеет вид
. Пусть последовательность вершин, образующих данный цикл, имеет вид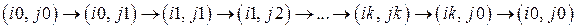 .
. знак “–”. Двигаясь вдоль цикла пересчета, будем в вершинах цикла поочередно ставить знаки “+” и “–”. Так как число вершин в цикле пересчета четно, то не важно в какую из соседних клеток совершен переход из клетки
знак “–”. Двигаясь вдоль цикла пересчета, будем в вершинах цикла поочередно ставить знаки “+” и “–”. Так как число вершин в цикле пересчета четно, то не важно в какую из соседних клеток совершен переход из клетки  . Эти поставки примут вид
. Эти поставки примут вид .
. подбирается таким образом, чтобы:
подбирается таким образом, чтобы: приняла максимально возможное значение.
приняла максимально возможное значение. в клетке
в клетке  . Тогда в качестве
. Тогда в качестве  , и по вершинам цикла пересчета согласно последовательности, перераспределить поставки. При этом поставка в клетке
, и по вершинам цикла пересчета согласно последовательности, перераспределить поставки. При этом поставка в клетке  , а сама клетка
, а сама клетка  ), сохраняя остальные в базисном плане с нулевыми значениями.
), сохраняя остальные в базисном плане с нулевыми значениями.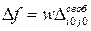 .
. , потребности получателей – вектором потребностей
, потребности получателей – вектором потребностей  . Матрица транспортных расходов имеет вид
. Матрица транспортных расходов имеет вид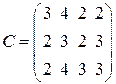 .
.
 .
.















 .
.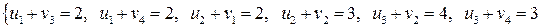
 имеет вид
имеет вид .
.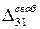 положительный:
положительный:
 ). Значит, данный базисный план не является оптимальным планом. Улучшим план, построив цикл пересчета. Клетку
). Значит, данный базисный план не является оптимальным планом. Улучшим план, построив цикл пересчета. Клетку 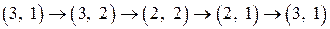 ,
, 100 50 –– + + ––
100 50 –– + + ––



 90
90  , которую необходимо поместить в клетку
, которую необходимо поместить в клетку  , из которой перемещается поставка
, из которой перемещается поставка  , станет свободной клеткой. В результате получаем базисный план, представленный в табл. 15.2.
, станет свободной клеткой. В результате получаем базисный план, представленный в табл. 15.2.





 ,
, .
.
 .
.
 положительный:
положительный:
 ,
, 70 130 60 – + 40 + 40 –
70 130 60 – + 40 + 40 –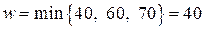 , которую необходимо поместить в клетку
, которую необходимо поместить в клетку  ).
).

