 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Правило сложения дисперсий
ВАРИАЦИОННЫЙ АНАЛИЗ Показатели вариации
Статистическая совокупность по определению включает однокачественные в пределах изучаемой закономерности и в то же время варьирующие единицы. Для того чтобы судить о типичности средней для данной совокупности, ее следует дополнить показателями, характеризующими вариацию величины изучаемого признака. В ряде случаев ряды распределения, построенные по одному и тому же признаку, могут при одной и той же величине его среднего уровня иметь разную степень вариации этого признака. Покажем это на следующем примере (табл. 5.1).
Таблица 5.1. Количество счетов физических лиц, обслуживаемых филиалами коммерческих банков (тыс. ед.)
Данные, приведенные в таблице 5,1, свидетельствуют о том, что среднее число обслуживаемых одним филиалом счетов физических лиц в каждом банке одинаковое – 5,7 тыс. ед. Вместе с тем различия (вариация) по количеству обслуживаемых счетов клиентов более резко выражены у филиалов банка 2, чем у филиалов банка 1. Вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени. Причиной вариации являются разные условия существования разных единиц статистической совокупности. Для измерения степени вариации единиц совокупности по изучаемому признаку используют абсолютные и относительные показатели вариации. К абсолютным характеристикам вариации относятся размах вариации (R), объем вариации (W), среднее линейное отклонение (d), дисперсия ( Относительные характеристики вариации рассчитываются как отношение абсолютных показателей степени вариации к среднему уровню изучаемого признака. Так, относительный размах вариации Размах вариации (R) равен разности между наибольшей (xmax) и наименьшей вариантами признака (xmin):
Этот показатель представляет интерес в тех случаях, когда важно знать пределы вариации признака, например пределы вариации ставок процента по кредитам и депозитам кредитных организаций одного и того же региона. Он востребован также при анализе инвестиционных проектов в условиях риска: из двух проектов тот считается более рискованным, у которого размах вариации экспертной оценки ожидаемого эффекта выше. Продолжая рассмотрение нашего примера, отметим, что при одной и той же величине среднего числа лицевых счетов физических лиц, обслуживаемых одним филиалом, размах вариации по этому показателю у филиалов банка 1 значительно меньше, чем у филиалов банка 2: 3,3 тыс. ед. против 10,9 тыс. ед. Деловая активность филиалов банка 2, очевидно, складывалась под влиянием более разнообразных условий, которые и определили резкие различия в масштабах их операций с клиентами. Следовательно, возникает вопрос, насколько точно рассчитанная для филиалов банка 2 средняя величина числа обслуживаемых счетов клиентов характеризует его индивидуальный уровень отдельных филиалов, т.е. вопрос о типичности средней. Однако характеристика степени вариации с помощью ее размаха является недостаточной, так как величина этого показателя зависит от значений только двух крайних вариант признака. Объем вариации исчисляется по формуле: - для несгруппированных данных
- для сгруппированных данных
Для обобщения всех различий величин признака в изучаемой совокупности используют показатели среднего линейного и среднего квадратического отклонений, которые имеют те же единицы измерения, что и варианты признака, и его средняя величина. Порядок расчета этих показателей для несгруппированных и сгруппированных данных различен. Среднее линейное отклонение (d) – это средняя арифметическая из абсолютных отклонений вариант признака от средней арифметической величины. Для расчета этого показателя применяют следующие формулы: - для несгруппированных данных
где
n – число единиц совокупности;
- для сгруппированных данных
В расчетах отклонения представлены без учета знака, так как по свойству средней арифметической сумма отклонений индивидуальных значений признака от средней равна нулю. Это ограничивает величину среднего линейного отклонения как меры вариации признака, за исключением тех случаев, когда суммирование показателей без учета знаков имеет экономический смысл. В связи с этим более широкое распространение в качестве показателя степени вариации получило среднее квадратическое отклонение. Среднее квадратическое отклонение является абсолютной мерой вариации и представляет собой корень квадратный из дисперсии. Смысловое содержание этого показателя такое же, как и среднего линейного отклонения: чем меньше его величина, тем однороднее совокупность и тем, соответственно, типичнее средняя величина. Дисперсией - для несгруппированных данных
- для сгруппированных данных
Формулы для расчета среднего квадратического отклонения имеют следующий вид: - для несгруппированных данных
- для сгруппированных данных
Формулу для расчета дисперсии можно преобразовать с учетом того, что
где или
Дисперсию и среднее квадратическое отклонение используют при расчетах связанных с организацией выборочного наблюдения, оценке полученных на основе выборки статистических показателей тесноты корреляционной связи, дисперсионном анализе. В условиях нормального распределения существует следующая зависимость между величиной среднего квадратического отклонения и количеством наблюдений: в пределах Отклонение В симметричных распределениях среднее квадратическое отклонение составляет приблизительно 1,25 среднего линейного отклонения. Это соотношение может быть использовано для приближенного вычисления среднего квадратического отклонения, исходя из уже найденного значения среднего линейного отклонения. При таких расчетах следует учитывать и полученные согласно правилу «трех сигм» следующие соотношения:
так как в нормальном распределении в размахе вариации «укладываются» Если распределение заведомо ассиметричное, то Рассмотрим порядок вычисления среднего линейного отклонения, дисперсии и среднего квадратического отклонения по приведенным выше несгруппированным данным о работе филиалов двух банков с клиентами (табл. 5.2). Используя приведенные выше формулы, получаем соответствующие абсолютные и относительные характеристики размера вариации (табл. 5.3). Таким образом, можно сделать вывод, что совокупность филиалов банка 1 имеет более низкий уровень их вариации по числу обслуживаемых счетов клиентов, чем совокупность филиалов банка 2, так как среднее квадратическое отклонение числа обслуживаемых клиентов по филиалам банка 1 составляет 2,17 тыс. ед., а по филиалам банка 2 – 4,40 тыс. ед.
Таблица 5.2. Данные расчета показателей
Таблица 5.3. Характеристики размера вариации
Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %. В нашем примере коэффициент вариации у банка 1 составил 38 %, а у банка 2 – 76 %.Так как у банка 1 коэффициент вариации незначительно превышает 33 %, можно предполагать, что среднее число обслуживаемых клиентов является типичным для филиалов этого банка и более точно отражает индивидуальные значения этого показателя у отдельных филиалов, чем у филиалов банка 2.
Способы расчета дисперсии
Для расчета дисперсии в интервальной группировке может быть использован метод моментов:
где i – величина интервала группировки; m1 – момент первого порядка; m2 – момент второго порядка;
A – центральная варианта группировки.
Для измерения вариации альтернативных признаков, которой свойственны лишь два противоположных варианта, рассчитывается так называемая дисперсия доли. Количественно вариация альтернативного признака проявляется в значении «0» у единиц совокупности, которые им не обладают, и в значении «1» у единиц, для которых он характерен. Ряд распределения по альтернативному признаку имеет вид:
Долю единиц (частость), обладающих данным признаком, обычно обозначают p, а не обладающих им – q. Средняя арифметическая такого ряда определяется следующим образом:
т.е. она равна относительной частоте (частости) p. Для альтернативного признака справедливо равенство: p + q = 1. Следовательно, q = 1 - p. Тогда дисперсия альтернативного признака (или дисперсия доли) исчисляется по формуле:
т.е. она равна произведению доли на дополняющее ее до единицы число. Рассмотрим следующий пример. Допустим, что при обследовании 1000 коммерческих банков 800 из них являются универсальными. Определить дисперсию и среднее квадратическое отклонение доли универсальных банков. Решение. В данном случае доля единиц, обладающих изучаемым признаком, т.е. доля универсальных банков а) б) Следовательно, дисперсия доли универсальных банков
Среднее квадратическое отклонение
Правило сложения дисперсий Правило сложения дисперсий гласит, что общая дисперсия (
Общая дисперсия отражает вариацию результативного признака, сложившуюся под воздействием всей совокупности причин и условий, определяющих его изменение. Она равна среднему квадрату отклонений отдельных значений результативного признака от его средней величины и может быть рассчитана по следующей формуле 5.6:
Межгрупповая дисперсия характеризует ту часть общей дисперсии, которая обусловлена делением совокупности на группы, т.е. отражает различия в величине изучаемого признака, которые возникают под влиянием одного условия, т.е. это вариация признака, положенного в основу группировки. Она равна среднему квадрату отклонений групповых средних
где
Средняя из внутригрупповых дисперсий характеризует остаточную вариацию, которая происходит под влиянием других, не связанных с группировкой факторов. Она вычисляется как средняя из внутригрупповых дисперсий (
Дисперсия в отдельных группах вычисляется по формуле:
Правило сложения дисперсий используют при определении степени точности типической выборки и измерении тесноты связи изучаемого результативного признака с признаками-факторами. Ряды распределения дают возможность выявить структуру исследуемой совокупности, но сами по себе не объясняют причин, определяющих изменение этой структуры. Для изучения влияния какого-либо фактора на результат необходимо оценить вариацию последнего, обусловленную влиянием исследуемого фактора. В аналитической группировке эту задачу решают на основе межгрупповой дисперсии. Очевидно, что чем больше доля межгрупповой дисперсии в общей, тем сильнее влияние группировочного признака-фактора на изучаемый результативный признак. Показателями тесноты связи служат коэффициент детерминации и эмпирическое корреляционное отношение. Коэффициент детерминации определяют как долю межгрупповой дисперсии в общей дисперсии признака-результата. Он показывает влияние изучаемого фактора х на часть общей вариации признака-результата y:
Эмпирическое корреляционное отношение – это корень квадратный из коэффициента детерминации:
Для оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:
Если связь между признаками отсутствует, то межгрупповая дисперсия равна нулю, а, следовательно, и коэффициент корреляции равен нулю. Таким образом, чем ближе значение показателя к единице, тем сильнее связь между признаками. Рассмотрим пример анализа зависимости объема активов коммерческих банков от срока их функционирования. Результаты группировки и промежуточные расчеты для определения показателей тесноты связи представлены в таблице 5.4.
Таблица 5.4. Данные расчета для определения показателей тесноты связи
Проверка правила сложения дисперсий:
Расчет показателей тесноты связи:
По изучаемой совокупности банков наблюдается высокая теснота связи между сроком их деятельности и объемом активов. Более 89 % различий в объеме активов банков определяется вариацией сроков их функционирования.
Вопросы и задания для самоконтроля 1. Что такое размах вариации и в чем его особенности как показателя вариации? 2. Назовите показатели, являющиеся абсолютными характеристиками степени вариации. 3. В чем состоят особенности расчета показателей вариации по сгруппированным данным? 4. Какое аналитическое значение имеет коэффициент вариации? 5. Что представляет собой дисперсия альтернативного признака? 6. Что представляет собой правило сложения дисперсий? 7. Как определяется внутригрупповая дисперсия? 8. Что характеризует межгрупповая дисперсия, формула ее расчета? 9. Что называется эмпирическим корреляционным отношением, и как оно интерпретируется?
|
) и среднее квадратическое отклонение ( 
).
; относительное линейное отклонение 
; коэффициент вариации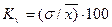 
.
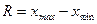. (5.1)
; (5.2)
. (5.3)
, (5.4)
- значение признака у i-той единицы совокупности;
- средняя величина признака в совокупности;
. (5.5)
; (5.6)
. (5.2)
; (5.8)
. (5.9)
, т.е. дисперсия равна разности средней из квадратов вариантов признака и квадрата их средней:
, (5.10)
(5.11)
. (5.12)
располагается 0,683 количества наблюдений;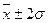 
– 0,954; 
– 0,997.
можно считать максимально возможным. Это положение называют правилом «тех сигм».
, (5.13)
( 
.
, (5.14)
; (5.15)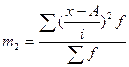
; (5.16)
, (5.17)
, (5.18)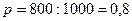
, или 80 %. Следовательно, 20 % банков не обладали изучаемым признаком. Эту величину можно получить двояко:
, или 20 %;
.
.
) и 2) среднюю из внутригрупповых дисперсий ( 
)
. (5.19)
от общей средней 
, (5.20)
- частота отдельных групп.
):
.
.
.
.
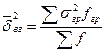), млн. руб.
]
)
;
;
;
.
.
;
.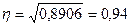