 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вычисление кратных интегралов.
Лекция 13 Понятие кратного интеграла и его свойства. Вычисление кратных интегралов. Понятие кратного интеграла и его свойства. Понятие кратного интеграла напрямую связано с понятием функции нескольких переменных. В рамках нашего курса рассмотрим двойные и тройные интегралы. Двойной интеграл определяется равенством:
Теорема (достаточное условие интегрируемости функции): Если функция Замечания: 1. Далее будем рассматривать только функции, непрерывные области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций. 2. Для интегрируемой в области
Теория тройного интеграла аналогична теории двойного интеграла. Тройной интеграл определяется равенством: . Здесь Теорема (существования): Если функция Свойства кратных интегралов: 1. Константа выносится вперед интеграла. 2. Интеграл от суммы функций равен сумме интегралов. 3. Разбиение области на части соответствует сумме интегралов. 4. 5. Если Аналогично если 6. Если функция где Аналогично где 7. Теорема (о среднем).Если подынтегральная функция непрерывна в замкнутой области . Величину называют средним значением функции Для тройного интеграла Вычисление кратных интегралов. Пусть требуется вычислить двойной интеграл, функция Вычисление двойного интеграла сводится к вычислению повторного интеграла
который вычисляется путем последовательного интегрирования. Сначала интегрируют внутренний интеграл, по переменной (2) Следует помнить, что внешние пределы интегрирования всегда постоянны, а внутренние, как правило, переменные. Пример: 1) Вычислить
2) Поменять пределы интегрирования
Двойной интеграл в полярных координатах. Пусть требуется вычислить двойной интеграл по обл.
Тогда двойной интеграл перепишется в виде: (3)
Замечание: 1. Переход к полярным координатам полезен, когда подынтегральная функция имеет вид 2.На практике переход к полярным координатам осуществляется путем замены уравнения линий, ограничивающих область Пример:Вычислить двойной интеграл
|




 непрерывна в замкнутой области
непрерывна в замкнутой области  , то она интегрируема в этой области.
, то она интегрируема в этой области.

 -
- непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области  , то предел интегральных сумм существует и не зависит от способа разбиения области
, то предел интегральных сумм существует и не зависит от способа разбиения области  непрерывна в замкнутой области
непрерывна в замкнутой области  , то
, то и
и 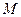 - соответственно наименьшее и наибольшее значения подынтегральной функции в области
- соответственно наименьшее и наибольшее значения подынтегральной функции в области  такая точка
такая точка  , что
, что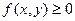 непрерывна в области D. Область D представляет собой криволинейную трапецию, ограниченную прямыми
непрерывна в области D. Область D представляет собой криволинейную трапецию, ограниченную прямыми  и
и  и кривыми
и кривыми 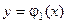 и
и 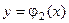 .
. , (1)
, (1) , считая переменную
, считая переменную  константой, а затем интегрируют по переменной
константой, а затем интегрируют по переменной  по области
по области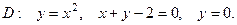



 .
. ,
, 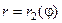
 ,
,  , причём
, причём  ; на
; на  ;
;  .
. ; область
; область  не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по  и
и  (исследуя закон изменения
(исследуя закон изменения  области
области  , если область D ограниченна линиями
, если область D ограниченна линиями  ,
,  , y=x, y=0.
, y=x, y=0.