ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Деление окружности на равные части.

1 2 34

Деление окружности на три равные части, и построение правильного вписанного треугольника выполняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

При делении окружности циркулем на три равные части из любой точки окружности, например из точки А пересечения центровых линий с окружностью (рисунок 15), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку А. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный.

а) б)

Рисунок 15 Рисунок 16

При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рисунок 16). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник.

При делении окружности на 12 частей циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рисунок 17).

а) б)

Рисунок 17

Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рисунке 18.

Половину любого диаметра (радиус) делят пополам (рисунок 18, а), получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рисунок 18, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности. Делая засечки на окружности (рисунок 18, в) радиусом R, равным отрезку 1В, делят окружность на пять равных частей.

а) б) в) г)

Рисунок 18

Сопряжения.

Сопряжение двух непараллельных прямых. Две непараллельные прямые располагаются друг к другу под утлом, который может быть прямым, тупым или острым. При выполнении чертежей деталей часто такие углы необходимо скруглить дугой заданного радиуса. Скругление углов на чертеже есть не что иное, как сопряжение двух непараллельных прямых дугой окружности заданного радиуса. Для выполнения сопряжения необходимо найти центр дуги сопряжения и точки сопряжения. Поскольку угол образован двумя прямыми, то проводят две линии центров параллельно каждой прямой на расстоянии, равном радиусу R дуги сопряжения (рисунок 21). Точка их пересечения будет центром дуги сопряжения.

а) б) в)

Рисунок 21

Для нахождения точек сопряжения из точки О опускают перпендикуляры на заданные прямее и получают точки сопряжения. Зная точки и центр сопряжения, из точки О радиусом R проводят дугу сопряжения. При обводке чертежа следует сначала обвести дугу, а затем касательные прямые.

Плавный переход одной окружности в другую может происходить или непосредственным касанием, или через третий элемент - дугу окружности.

Касание двух окружностей может быть внешним (рисунок 22, а) или внутренним (рисунок 23 а).

Внешнее касание. При внешнем касании двух окружностей расстояние между центрами этих окружностей будет равно сумме их радиусов (рисунок 22).

Например, требуется построить плавный переход от окружности радиуса R к окружности радиуса R₁ с внешней стороны, точка касания не задана. К окружности радиуса R можно построить множество касательных окружностей радиуса R₁ с внешним касанием (рисунок 22, б). Их центры (О₁, О₂ и т. д.) будут находиться от центра О на одинаковом расстоянии, т. е. на окружности радиуса R2 =R + R1, проведенной из центра О заданной окружности. Точки касания

К, K₁ и т. д. лежат на прямых, соединяющих центры сопрягающихся окружностей (рисунок 22, б).

На рисунке 22, в показано построение внешне-1 го касания двух окружностей с произвольно выбранной точкой касания К.

а) б) в)

Рисунок 22

Внутреннее касание. При внутреннем касании двух окружностей одна из касательных окружностей находится внутри другой окружности, и расстояние между центрами этих окружностей будет равно разности их радиусов (рисунок 23).

Сопряжение двух окружностей дугой заданного радиуса может быть внешним, внутренним и смешанным.

Внешнее сопряжение двух заданных окружностей дугой заданного радиуса. Даны две окружности радиусов R и R₁, (рисунок 24, а), требуется построить внешнее сопряжение дугой радиуса R₂. Известно, что для окружности радиуса R центр дуги сопряжения находится на линии центров, проведенной суммой радиусов R + R₂ из центра О. Для окружности радиуса R₁ центр дуги сопряжения лежит на линии центров, проведенной радиусом R₄ = R₁ + R₂ из центра O1. Эти окружности (линии центров) проводят не полностью, а только до взаимного пересечения в точке О₂ (рисунок 24, а). Точка О₁ будет центром дуги сопряжения. Точка сопряжения лежит .на прямой, соединяющей центр дуги сопряжения с центром заданной окружности, поэтому, соединяя точку О₂ с точками О и О₁ (рисунок 24, б), в пересечении с заданными окружностями получают точки сопряжения К и K1. Из точки O₁ радиусом R₂ от точки К до точки К₁ проводится дуга сопряжения.

Внутреннее сопряжение двух окружностей дугой заданного радиуса. Сопрягаемые окружности располагаются внутри сопрягающей дуги, и центр сопрягающей дуги будет находиться от центров заданных окружностей на расстоянии, равном разности радиусов (дуги и соответствующей окружности).

Рисунок 24

Даны две окружности с радиусами R и R₁ (рисунок 25, а), требуется построить внутреннее сопряжение дугой радиуса R₂ в верхней части. Известно, что для окружности радиуса R центр дуги сопряжения находится на линии центров, проведенной радиусом R₃ = R₂ — R из центра О заданной окружности. Для окружности радиуса R₁ центр дуги сопряжения находится на линии центров, проведенной радиусом R₄ = R₂ – R₁ из центра O₁ заданной окружности. В нижней части чертежа из центров О и O₁ радиусами R₃ и R₄ проводят дуги до взаимного пересечения в точке О₂, которая будет центром дуги сопряжения, так как является общей точкой для двух линий центров (рисунок 25, а). Находят точки сопряжения. Для этого точку O₂ (центр дуги сопряжения) соединяют с точками О и O1 прямыми линиями, которые продлевают до пересечения с заданными окружностями в точках К и К₁, которые будут точками сопряжения (рисунок 25, б).

Даны две окружности с радиусами R и R₁ (рисунок 26), требуется построить сопряжение дугой радиуса R₂ так, чтобы с окружностью радиуса R было внешнее касание, а с окружностью радиуса R₁ - внутреннее. Из центра О проводят дугу (линию центров) радиусом R₃, равным R+R₂ (рисунок 26), а из центра О₁ - линию центров радиусом R₄, равным R₂ – R₁ (рисунок 26). В пересечении линий центров получают точку О₂ (центр дуги сопряжения). Для нахождения точек сопряжения центр дуги сопряжения O₂ соединяют с центрами О и O₁ прямыми. Прямую О₂ O₁ продолжают. В пересечении этих прямых с заданными окружностями получают точки сопряжения К и К₁ Из точки O₂ дугой радиуса R₂ от точки К до точки K₁ проводят дугу сопряжения (рисунок 26).

Заданы прямая и дуга окружности R , требуется построить сопряжение дугой радиуса R1.

Рисунок 25 Рисунок 26

Лекальные кривые.

Лекальные кривые называют так потому, что они обводятся по лекалу.

Построение эллипса по заданным осям. Заданы оси эллипса АВ (большая) и CD (малая), требуется построить эллипс. Проводят две взаимно перпендикулярные прямые и от точки их пересечения (точка О) откладывают вверх и вниз по половине малой оси, а влево и вправо - по половине большой оси (рисунок 27). Из точки О описывают две концентрические окружности: одну - через концы малой оси, а вторую - через концы большой оси. Большую окружность делят на любое число равных частей, например, двенадцать, все точки деления соединяют прямыми с точкой О. Эти двенадцать радиусов разделяют малую окружность тоже на двенадцать равных частей. Из всех двенадцати точек, лежащих на большой окружности, проводят прямые, параллельные малой оси, а из точек, лежащих на малой окружности, проводят прямые, параллельные большой оси эллипса, до пересечения друг с другом. В пересечении этих прямых получают точки, принадлежащие эллипсу. Затем эти точки соединяют от руки плавной линией и обводят по лекалу.

Рисунок 27

Циклоида (от греч. kykloeides - кругообразный) - плоская кривая, описываемая точкой окружности, которая без скольжения катится по прямой линии.

Заданы направляющая прямая CD и производящая окружность радиуса R с лежащей на ней точкой К, исходное положение которой Ко (рисунок 29). Проследим, какой путь пройдет точка К за один полный оборот окружности, катящейся по прямой CD. Это будет полный цикл кривой. Окружность за это время пройдет по прямой путь, равный длине развернутой окружности, т. е. L=2πR. Точка К после одного оборота окружности снова окажется на прямой CD в точке K₈.

Для определения промежуточных положений точки К. через равные промежутки фиксируют положение этой точки. Для этого делят окружность на любое число равных частей, например, на восемь, получают точки 1...8 (рисунок 29), проводят из точки О линию центров, на которой отмечают восемь промежуточных положений центров (O₁ O₈) производящей окружности, разделив L=2πR на восемь равных частей.

Когда окружность пройдет 1/8 своего пути, точка К сместится вправо и вверх и окажется над направляющей прямой CD на такой же высоте, на которой находится точка 1. Поэтому для построения промежуточной точки К₁ из точки 1 проводят прямую, параллельную CD, а из центра O₁ описывают часть окружности в ее промежуточном положении радиусом R до пересечения с этой прямой.

Это и будет первое промежуточное положение точки К. Аналогично строят остальные точки. Соединив точки К₀...K₈ плавной тонкой линией от руки, получают циклоиду, которую обводят по лекалу.

Рисунок 29

Спираль Архимеда — кривая, образованная движением точки, равномерно движущейся по прямой, которая, в свою очередь, равномерно вращается в плоскости вокруг неподвижной точки, принадлежащей этой прямой. Характер спирали Архимеда определяется шагом t, т. е. перемещение прямой может происходить как по часовой стрелке, так и против.

Рисунок 30

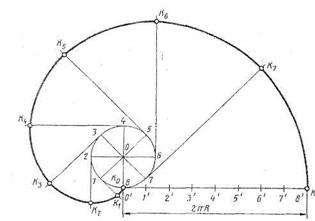
Чтобы построить спираль, необходимо зафиксировать несколько промежуточных положений точки и прямой, по которой она перемещается. Для этого вспомогательная окружность, проведенная радиусом, равным t и отрезок О8, равный шагу, делятся на одинаковое число равных частей, например, на восемь (рисунок 30). Начальная точка (Ко) совпадает с точкой О. Отрезок O8, по которому движется точка, вращается так, что один конец (точка О) неподвижен. При повороте отрезка на 1/8 полного угла (45°) точка К пройдет 1/8 своего пути. Поэтому если из центра О радиусом O1 провести дугу до пересечения с прямой, проведенной через точку 1' и центр О, получим точку К₁ принадлежащую спирали. Если провести дугу радиусом O2 до пересечения с прямой O2', получится точка K₂, принадлежащая спирали, и т. д. При полном обороте отрезка O8 вокруг точки О отрезок совпадает со своим начальным положением, а точка К займет положение K₈.

Эвольвента окружности — плоская кривая линия, представляющая собой траекторию точки окружности при ее развертывании. Слово «эвольвента» — латинское, означает «развертывающий».

Заданную окружность делят на любое число равных дуг (в данном случае на восемь), получают точки 1...8. Каждую точку деления соединяют с центром окружности (точка O). Из точки 8 проводят касательную к окружности и откладывают на ней длину окружности (2teR). Этот отрезок будет развернутой окружностью. Точка 8 будет принадлежать эвольвенте. Затем полученный отрезок делят на восемь равных частей и получают отрезки, равные 1/8 длины окружности, для определения длины каждой развернутой дуги. Далее через точки 1...8 проводят касательные и откладывают отрезки, равные длине соответствующей дуги. От точки 1 откладывают отрезок, равный длине развернутой дуги О' 1'. От точки 2 — отрезок, равный длине развернутой дуги O'2' и т. д. Получают точки К¹ ... К⁸, принадлежащие эвольвенте. Полученные точки соединяют плавной кривой линией, которую обводят по лекалу.

Рисунок 31

1 2 34