 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Паралельний коливальний контур
Послідовний коливальний контур Розрахункова схема послідовного навантаженого контура наведена на рис. 4.9.
а) б)
а) розгалужений, б) нерозгалужений
Рисунок 4.9 – Послідовний навантажений коливальний контур
Вихідні дані: Vm=110 B; L=0.3*10-3 Гн; R=60 Ом; C=0.25*10-9 Ф; RH=60 кОм. 4.2.1 Визначаємо кутову резонансну частоту ωp та хвильовий опір ρ: ωp= де L, C – еквівалентні індуктивність і ємність контура СЕКВ= 0,5С+0,5С=С
4.2.2 Добротність ненавантаженого Q та навантаженого опором RH контура:
де внесений опір RВH:
4.2.3 Розрахунок межових частот та смуги пропускання для навантаженого і ненавантаженого контура. Верхня і нижня частоти смуги пропускання ненавантаженого контура:
де затухання контура d дорівнює:
Відносна смуга пропускання:
Для навантаженого контура смуга пропускання збільшиться:
Верхня і нижня межові частоти смуги пропускання навантаженого контура:
4.2.4 Комплексний вхідний опір для ненавантаженого і навантаженого контура. При резонансі :
На границях смуги пропускання коливального контура активні та реактивні опори рівні за величиною
- де
де
Для навантаженого контура:
Комплексний опір для межових частот:
де
4.2.5 Визначаємо комплексним методом струм і напругу на всіх ділянках навантаженого контура для верхньої частоти, при умові За законом Ома: На верхній межовій частоті Комплексна амплітуда струму:
Комплексна напруга
Струм у навантаженні:
Струм в ємності (рис. 4.9):
Комплексна напруга на ділянці bd:
Комплексна напруга на індуктивності:
4.2.6 Миттєві значення струмів та напруг, знайдені в п. 4.2.5:
u u u u 4.2.7 Векторна діаграма напруг та струмів для верхньої межової частоти навантаженого контура подана на рис. 4.10. Обираємо масштаби напруг та струмів:
Рисунок 4.10 – Векторна діаграма напруг та струмів.
Модуль струму I дорівнює:
де Розділивши знайдений струм на значення струму при резонансі:
отримуємо нормовану величину струму:
При малих розстроюваннях контура:
Розрахункові дані для побудови АЧХ і ФЧХ навантаженого і ненавантаженого коливального контурів наведені в таблиці 4.2.
Таблиця 4.2 – Розрахункові дані для побудови АЧХ і ФЧХ.
Продовження таблиці 4.2
Для побудови фазочастотної характеристики (ФЧХ) скористуємося узагальненим розстроюванням контура
Фазовий кут:
Розрахункові дані наведені в таблиці 4.2. За результатами розрахунків на рис. 4.10 побудована АЧХ, а на рис. 4.11 побудована ФЧХ.
Рисунок 4.11 – Амплітудно-частотна характеристика: 1 – для ненавантаженого контура; 2 – для навантаженого.
Рис. 4.12 – Фазочастотна характеристика: 1 – для ненавантаженого контура; а 2 – для навантаженого. Паралельний коливальний контур Розрахункова схема паралельного коливального контура наведена на рис. 4.13.
Рисунок 4.13 – Паралельний коливальний контур 4.3.1 Визначаємо резонансну частоту контура:
або за наближеною формулою:
де 4.3.2 Добротність контура.
Коефіцієнт вмикання:
4.3.3 Межові частоти і ширина смуги пропускання. Нижня гранична частота:
Верхня гранична частота:
Ширина смуги пропускання:
4.3.4 Розрахунок комплексного вхідного опору при резонансі і на межах смуги пропускання. 4.3.4.1 На резонансній частоті:
Еквівалентний комплексний опір
4.3.4.2 Нижня гранична частота
4.3.4.3 Верхня гранична частота
4.3.5 Визначаємо струми у паралельних вітках при частоті резонансу струмів
4.3.6 Визначаємо частоту резонансу напруг у вітці з ємністю:
4.3.7 Частотні характеристики відносних значень опорів у функції Активний вхідний опір визначається:
де
Реактивний вхідний опір:
Повний вхідний опір:
Відносні значення активного, реактивного і повного опорів:
За (4.3.7.1)...(4.3.7.3) будуємо частотні характеристики відносних значень опорів (рис. 4.14) Розрахункові дані занесені в таблицю 4.3
Таблиця 4.3 – Розрахункові дані для побудови частотних характеристик відносних значень опорів
Рисунок 4.14 – Частотні характеристики відносних значень опорів: 1 - 4.3.8 Будуємо амплітудно-частотні характеристики передаточних функцій зі струму для паралельних віток контура:
Розрахункові дані за (4.3.8.1) і (4.3.8.2) занесені до таблиці 4.3.2.
Таблиця 4.4 – Розрахунок АЧХ передаточних функцій зі струму
На рис. 4.15 надані АЧХ передаточних функцій зі струму.
Рис. 4.15 – АЧХ передаточних функцій зі струму паралельних віток: 1 - KLI(w); 2 – KCI(w)
|
,
(кОм)
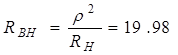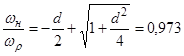
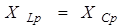
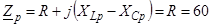(Ом)
(Ом)
. Відповідно і фазовий зсув 
між напругою на затискачах кола та струмом складає 
- узагальнене розстроюванням контура
,
.
при 
, тоді початкова фаза напруги мережі теж буде дорівнювати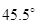 
, тобто 
(рис. 4.9) :
(В), де 
;
;
;
;
;
;
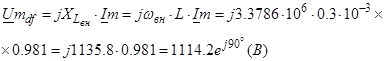
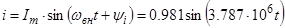4.2.8 Побудова резонансної кривої струму (АЧХ) I/IP:
град
град
.
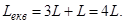
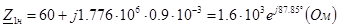
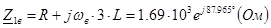
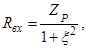
- активний опір при резонансі,
- узагальнене розстроювання контура
(4.3.7.1)
(4.3.7.2)
(4.3.7.3)
; 2 - 
(4.3.8.1)
(4.3.8.2)
