 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Т. 2. Теорема Ферма (необходимое условие экстремума).
Монотонность функции. Исследование на экстремум Т. 1. (О производной монотонной функции) 1) Если функция 2) Если функция Д-во. 1) 2) Геом. смысл теоремы: Если Т. 2. Теорема Ферма (необходимое условие экстремума). Если: 1) Д-во. Пусть а) Если б) Если Следовательно, Вывод: в точках, в которых Зам. 1: Из того, что Зам. 2: Функция ПР. ПР. Опр. Точки области определения функции Очевидно, что не во всякой критической точке 1-го порядка функция имеет экстремум. Однако, если в некоторой точке функция имеет экстремум, то это обязательно критическая точка.
Д-во. Обозначим
Аналогично можно доказать, что если Замечание. Если при переходе слева направо через точку Правило отыскания локальных экстремумов функции 1.Найти область определения функции 2.Найти критические точки 1-го порядка. 3.Нанести на числовую ось 4.Выделить критические точки, при переходе через которые 5.Вычислить значения ПР. ПР. ПР. Т.4. (Второе достаточное условие существования экстремума) Если функция Д-во. Пусть Замечание. Если ПР. Замечание.. Второе достаточное условие можно обобщить: пусть Если n-четное, то экстремум есть; если n- нечетное, то экстремума нет. При этом, если
Т.5. (Достаточное условие выпуклости графика функции) Если функция
Д-во:По определению выпуклой вверх кривой все ее точки на
запишем теорему Лагранжа: а) б) Аналогично доказывается достаточное условие выпуклости вниз. (сами!) ПР. Опр. Точка кривой, при переходе через которую кривая меняет направление выпуклости, называется точкой перегиба. Касательная в точке перегиба пересекает график!!! (+ рис.) Т. 6. (Необходимое условие перегиба) Если
Замечание 2: В точке перегиба Опр.Точки области определения функции Т. 7. (Достаточное условие перегиба) Пусть функция ПР. 1. ПР.2. ПР.3. Асимптоты.
ПР. Пусть прямая
Найдем Если хотя бы один из пределов (1) или (2) не существует или бесконечен, то наклонной асимптоты при При ПР.
§4. Общая схема исследования ф-ции и построения графика. 1.Исследование вида зависимости 1) область определения; 2) точки разрыва; 3) четность и нечетность; 4) точки пересечения с осями координат; 5) периодичность; 6) исследование поведения функции на концах области определения; 7) асимптоты: а) вертикальные; б) наклонные. 2.Исследование по первой производной: 1) критические точки 1-го порядка; 2) участки монотонности; 3) точки локальных экстремумов. 3.Исследование по второй производной: 1) критические точки 2-го порядка; 2) участки выпуклости и вогнутости; 3) точки перегиба. 4.Построение графика с учетом результатов, полученных в пунктах 1-3. Пр. 1) 1.1) 2) непрерывна; 3) 4) 5) непериодическая 6) 7) а) функция непрерывна Þ вертикальных асимптот нет; б) 2. 1) критические точки 1-го порядка:
3) экстремумов нет. 3. a)критические точки 2-го порядка:
b) c)
ПР. 2. 1.1) 2) непрерывна; 3) функция общего вида; 4) 5) непериодическая; 6) 7) а) функция непрерывна Þ вертикальных асимптот нет; б) 2. 1) критические точки 1-го порядка: 2)
3) 3. 1) критические точки 2-го порядка:
2)
4.
Пр. 4. 1.1) 2) 3) нечетная; 4) 5) непериодическая; 6) 7) а) б) 2. 1)
2)
3. 1)
3) точка перегиба: 4.
Глобальный экстремум Если Правило: чтобы найти наибольшее и наименьшее значения 1) найти все точки локальных экстремумов 2) вычислить 3) из всех полученных значений Пр. Найти наибольшее и наименьшее значения |



 дифференцируема на
дифференцируема на  и возрастает (убывает) на
и возрастает (убывает) на  , то
, то 

 .
.

 ,
,  .
.  при
при  и
и  при
при 
 в обоих случаях
в обоих случаях 
 . По теореме Лагранжа о конечных приращениях имеем:
. По теореме Лагранжа о конечных приращениях имеем:  :
:  . Т.к.
. Т.к. 


 в любой точке отрезка
в любой точке отрезка  .
. экстремум, то
экстремум, то  .
. – точка локального максимума. Тогда
– точка локального максимума. Тогда  :
: 
 . Пусть
. Пусть  . Тогда
. Тогда  или
или  .
. при некотором
при некотором  ). Тогда для
). Тогда для 
 .
.
 , может быть экстремум (а может и не быть!).
, может быть экстремум (а может и не быть!). , еще не следует, что
, еще не следует, что  – точка локального экстремума.
– точка локального экстремума. не существует или равна
не существует или равна 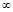 .
. . В точке
. В точке  функция не дифференцируема, но имеет минимум.
функция не дифференцируема, но имеет минимум. . В точке
. В точке  , но экстремума в ней нет.
, но экстремума в ней нет. Т.3. (Первое достаточное условие существования экстремума)Пусть
Т.3. (Первое достаточное условие существования экстремума)Пусть  ;
; .
.


 и
и 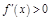
 , то
, то  .
. – критическая точка 1-го порядка, но
– критическая точка 1-го порядка, но  . Следовательно, экстремума нет.
. Следовательно, экстремума нет. не существует
не существует  – критическая точка 1-го порядка;
– критическая точка 1-го порядка; 
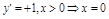 – точка минимума.
– точка минимума. . Найти экстремумы.
. Найти экстремумы. ,
,  , то в точке
, то в точке  , и минимум, если
, и минимум, если  .
.
 при
при 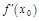 не существует, то
не существует, то  тоже не существует и вопрос о существовании экстремума решается по первому достаточному условию.
тоже не существует и вопрос о существовании экстремума решается по первому достаточному условию.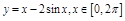 .
.  .
. 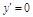 при
при  .
. 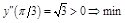 ,
,  .
. =
=  .
.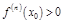 , то min; если
, то min; если  – max.
– max. §2. Направление выпуклости. Точки перегиба.
§2. Направление выпуклости. Точки перегиба. Опр. Непрерывная кривая называется выпуклой вверх (выпуклой) на
Опр. Непрерывная кривая называется выпуклой вверх (выпуклой) на  , если все ее точки лежат ниже любой ее касательной на этом интервале.
, если все ее точки лежат ниже любой ее касательной на этом интервале. Опр. Непрерывная кривая называется выпуклой вниз (вогнутой) на
Опр. Непрерывная кривая называется выпуклой вниз (вогнутой) на  имеет
имеет 
 и
и 
 .
. Геометрическое пояснение:
Геометрическое пояснение:  возрастает, значит,
возрастает, значит,  увеличивается.
увеличивается.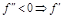 убывает, значит,
убывает, значит,  Правило для запоминания:
Правило для запоминания: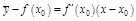

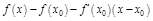 Для разности
Для разности 
 точка с:
точка с: 

 . По еореме Лагранжа
. По еореме Лагранжа  т.
т.  :
:  .
. , но
, но 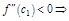
 .
. , но
, но 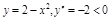 . Следовательно, кривая выпукла вверх.
. Следовательно, кривая выпукла вверх.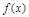 определена и дважды дифференцируема в некоторой окрестности точки
определена и дважды дифференцируема в некоторой окрестности точки  – точка перегиба, то
– точка перегиба, то  . (+ рис.)
. (+ рис.) Замечание 1: Из того, что
Замечание 1: Из того, что  , еще не следует, что
, еще не следует, что  может не существовать или быть равной
может не существовать или быть равной  либо
либо  терпит разрыв, называются критическими точками 2-го порядка.
терпит разрыв, называются критическими точками 2-го порядка.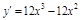 ,
,  .
. ;
;  ;
; 
 .
.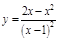 ;
;  ;
; 
 .
.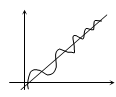 Опр. Прямая наз-ся асимптотой кривой, если расстояние
Опр. Прямая наз-ся асимптотой кривой, если расстояние  от переменной точки
от переменной точки  кривой до этой прямой при удалении точки
кривой до этой прямой при удалении точки  .
. Замечание.Прямая
Замечание.Прямая  является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  или
или 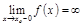 , т.е. точка
, т.е. точка 
 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  . Найдем
. Найдем  и
и  .
.

 .
.  ,
, 




 (1)
(1)
 (2)
(2) нет.
нет.
 . Найти асимптоты графика.
. Найти асимптоты графика. – вертикальная , а
– вертикальная , а 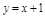 – наклонная асимптота.
– наклонная асимптота.
 ;
; – функция общего вида;
– функция общего вида; ;
; ,
, 

 .
.
 ;
;
 – – –
– – –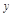 0 1 x
0 1 x

 + – +
+ – + 0
0  1
1  точки перегиба:
точки перегиба: 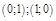
 .
.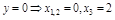 ;
; ,
,  ;
;
 - наклонная асимптота.
- наклонная асимптота.
 ;
;
 .
.

 3) точка перегиба:
3) точка перегиба:  .
. ПР.3.
ПР.3. 
 ;
;  ;
;  – ас-ты,
– ас-ты,  – min,
– min,  – перегиб.
– перегиб.
 ;
; – т. разрыва 2-го рода;
– т. разрыва 2-го рода; ;
;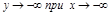 ,
,  ;
; ,
,  ,
,  ,
,  ;
;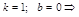
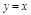 - наклонная асимтота.
- наклонная асимтота.
 ;
;
 -2 0 2
-2 0 2  x
x ;
; 3)
3)  – точки максимума и минимума;
– точки максимума и минимума; 




 2)
2)  .
. , то своего наибольшего (наименьшего) значения она может достигать либо в точке локального экстремума, принадлежащей
, то своего наибольшего (наименьшего) значения она может достигать либо в точке локального экстремума, принадлежащей  , либо на конце отрезка.
, либо на конце отрезка. и
и  (значения на концах области определения);
(значения на концах области определения); на отрезке
на отрезке  . Ответ:
. Ответ:  .
.