 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Рекомендации для выполнения 12
КОНТРОЛЬНАЯ РАБОТА №1 По дисциплине «Метрология, стандартизация и сертификация» 1 часть - метрологическая оценка результата косвенного измерения Задания для выполнения Заданы ряды результатов равноточных измерений исходных физических величин. Необходимо провести метрологическую оценку результата конкретного косвенного измерения, согласно варианту. Таблица 4.1 1 вариант
2 вариант
3 вариант
4 вариант
5 вариант
6. вариант
7 вариант.
8. вариант
9. вариант
10. вариант
Порядок выполнения метрологической оценки результата измерения
Целью любых измерений является получение численного результата, то есть значения физической величины, найденного путем ее измерения. Однако, на практике не удается получить значение физической величины, которое бы идеальным образом отражало ее истинное значение. В связи с этим возникает проблема оценки того, насколько результат измерения отклоняется от истинного значения измеряемой величины, то есть проблема определения погрешности измерения. Правила округления результатов измерений и вычислений Результат любого точного измерения всегда выражается двумя числами: числовым значением измеряемой величины и параметром точности -- результатом определения погрешности. Например, запись результата измерения активного сопротивления R = 40,78 + 0,01 Ом. Обычно погрешность выражают не более двумя значащими цифрами. Округление результата должно производиться в полном соответствии с погрешностями (параметрами точности) результата. Числовое значение результата непременно должно оканчиваться десятичным знаком того же разряда, что и погрешность. Таблица 4.2 - Значения распределения Стьюдента
При округлении следует руководствоваться следующими правилами: - лишние значащие цифры у целых чисел заменяются нулями, а у десятичных дробей отбрасываются; - если цифра старшего (который левее) из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяются; - если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на 1; - если отбрасываемая цифра равна 5, а следующие за ней цифры нули, то последнюю сохраняемую цифру не изменяют, если она четная, и увеличивают на 1, если она нечетная. Примеры результатов измерений до и после округления: - до округления X, = 1001,77 ± 0,033, после округления X, = 1001,770 ± 0,033; или 1001,77 ± 0,03; - до округления Х2 = 237,465 ± 0,127, после округления Х2 = 237,46 ±0,13; - до округления Х3 = 123357 ± 678, после округления Х3= 123400 ±700. Рекомендации для выполнения В качестве примера рассмотрим выполнение метрологической оценки результата косвенного измерения действительной постоянной счетчика электрической энергии где Р - мощность, t - время, N — количество оборотов диска. Ряды результатов равноточных измерений исходных физических величин:
1) Вычисляем значения действительной постоянной k счетчика ki = Pi .ti / Ni
(2200+2052+…+2221)/10 = 2186 Дж/об 3) Определяем погрешность каждого измерения Δki
{|13,8| + |-133,9| + …+|34,8|}/10 = 104,6 Дж/об 5) Определяем среднюю квадратическую погрешность единичного измерения:
Дж/об
6)Выполняем проверку соотношения между r и S: S/r =144,4 / 104,6 = 1,38 Вывод: так как п = 10 < 30, то и условие S/r = 1,25 выполняется приблизительно. 7) Определяем среднеквадратическое отклонение среднеарифметического значения Skср. 8) Доверительный интервал Δk определяем при доверительной вероятностиP(t,n) =0,95. Коэффициент Стьюдента при 10 измерениях и при P(t,n) =0,95 равен t9 = 1,8331. Тогда Следовательно, значение действительной постоянной k счетчика лежит в диапазоне от 2104,45 до 2269,89 Дж/об и результат измерений нужно записать как k = kср + Δk = 2186 + 83,7 Дж/об Этот расчет проведен для определения как для прямого измерения одной величины. Однако здесь на самом деле проходили измерения во всяком случае двух групп взаимно независимых величин: мощности тока P с одной стороны, а с другой - число оборотов N и времени t, которые все-таки имеют прямую взаимосвязь. Часто требуется рассчитать погрешность измерения как погрешность косвенных измерений нескольких величин. Связь между погрешностями определения отдельных величин и результирующей искомой величины будет в общем описываться зависимостями (см.табл. 4.3): Таким образом, необходимо проведение расчета по всему вышеуказанному алгоритму отдельно для каждой величины: для мощности Р, времени t и числу оборотов N. Так, вычисляем среднеарифметические величины. Получим значения: Определим среднюю абсолютную погрешность: ΔР =5,88 Вт; Δt = 7,24 c; ΔN = 2 оборота. Определим среднюю квадратичную погрешность: SР = 7,69 Вт; St = 9,50 c; SN = 2,58 оборота. Отношения средней квадратичной погрешности к абсолютной: SР /ΔР = 1,31; St /Δt = 1,31; SN /ΔN = 1,29. Средняя квадратичная погрешность среднеарифметической величины SРср = 2,43; St ср = 3,00; SNср = 0,82. Доверительный интервал для каждой независимой величины будет ΔРср = 4,458 Вт; Δ S ср = 5,506 с; ΔNср = 1,497 оборотов. Вопрос, как влияют погрешности измерений отдельных величин на общий результат в данное время является дискуссионным. Формулы, приведенные в табл. 4.3, представляют собой представления одной из наиболее авторитетных школ. Так, согласно табл. 4.6
Абсолютная погрешность Относительная погрешность будет
Табл.4.3
Для частного (деления) из двух величин АВ/С имеем:
Относительная погрешность будет
Тогда абсолютная погрешность действительной постоянной k будет:
Доверительный интервал также может быть вычислен по той же формуле, вместо значений абсолютной погрешности отдельных величин значениями их доверительных интервалов, тогда получаем Δkcp=+ 124,1 Дж/об. Тогда результат определения действительной постоянной k счетчика должен быть представлен как k = kcp+ Δkcp = 2186 + 124,1 Дж/об. Сравним этот результат с результатом, полученным как по прямому определению искомой величины, k = kср + Δk = 2186 + 83,7 Дж/об. Видно, что учет погрешностей отдельных величин при косвенном определении искомой величины дает существенно больший доверительный интервал.
ЧАСТЬ - ПОГРЕШНОСТИ. 12 |



 ,
, 2) Определяем среднее арифметическое постоянной kср
2) Определяем среднее арифметическое постоянной kср 4) Определяем среднюю арифметическую погрешность единичного измерения
4) Определяем среднюю арифметическую погрешность единичного измерения


 214,6 Вт;
214,6 Вт;  304,3 c;
304,3 c;  30 оборотов.
30 оборотов. для произведения трех величин А, В и С имеем:
для произведения трех величин А, В и С имеем:

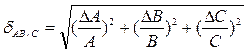 Абсолютная погрешность
Абсолютная погрешность 
