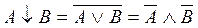ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Дизъюнктивная нормальная форма (ДНФ). 12
Конъюнкция называется элементарной, если в ней каждая переменная встречается не более одного раз. Дизъюнкция (сумма) элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ). Дизъюнктивная совершенная нормальная форма (ДСНФ). Алгоритм перехода от табличного задания функции к ДСНФ. 1. Выбрать в таблице все наборы аргументов, при которых функция обращается в 1 (множество Т1). 2. Выписать конъюнкции, соответствующие этим наборам аргументов. При этом, если аргумент входит в данный набор как 1, он вписывается без изменения в конъюнкцию, соответствующую данному набору. Если аргумент входит как 0, то в конъюнкцию вписывается его отрицание.
Выпишем ДНФ: F(x, y, z) =
Конъюнктивная нормальная форма (КНФ). Дизъюнкция называется элементарной, если в ней каждая переменная встречается не более одного раз. Конъюнкция (произведение) элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ). Конъюнктивная совершенная нормальная форма (КСНФ). Алгоритм перехода от табличного задания функции к КСНФ. 1. Выбрать в таблице все наборы аргументов, при которых функция обращается в 0 (множество Т0). 2. Выписать дизъюнкции, соответствующие этим наборам аргументов. При этом, если аргумент входит в данный набор как 0, он вписывается без изменения в дизъюнкцию, соответствующую данному набору. Если аргумент входит как 1, то в дизъюнкцию вписывается его отрицание.
Выпишем КНФ: F(x, y, z) = ( ПРАКТИЧЕСКАЯ ЧАСТЬ. 1. Определить ДНФ, ДСНФ, КНФ и КСНФ ФАЛ, для которых составлены таблицы истинности
«АНАЛИТИЧЕСКИЙ МЕТОД МИНИМИЗАЦИИ ФАЛ и ГРАФИЧЕСКИЙ МЕТОД МИНИМИЗАЦИИ ФАЛ С ПОМОЩЬЮ КАРТ КАРНО » ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Карты Карно – графический метод отображения булевых функций. Это специальные таблицы, задающие ФАЛ. Они сформированы так, чтобы облегчить процесс склеивания. Карты Карно используются при n – 2, 3, 4, 5, 6, при n > 6 они практически не используются. Основные принципы построения карт Карно: В карте Карно две соседние клетки, помеченные символами 1, всегда соответствуют конъюнктивным членам ДНФ, отличающимися только одним сомножителем. Поэтому их можно слить. Причем отличающийся сомножитель при слиянии поглощается. Процесс слияния и поглощения можно расширять разными способами: Во-первых, следует учитывать, что противоположные края условны, т.е. клетки на противоположных краях можно объединять так же, как если бы они находились в средней части карты. Во-вторых, можно сливать не только 2, но и 4, 8 и т.д. соседних клеток. При слиянии 2 клеток поглощается 1 переменная. При слиянии 4 клеток поглощается 2 переменные. При слиянии 8 клеток поглощается 3 переменные. Правила упрощения булевых функций с помощью карт Карно: Среди всех маркированных клеток (т.е. клеток, соответствующих наборам переменных, на которых функция имеет значение 1) следует отыскать такие, которые совместно образуют наибольшую область размером 2, 4 или 8 клеток и окружить эту область контуром. Необходимо выбрать дополнительные блоки маркированных клеток, которые имеют максимальный размер, причем количество таких блоков должно быть минимальным, но каждая маркированная клетка должна войти хотя бы в один блок. При оконтуривании групп разрешается одну и ту же маркированную клетку включать более чем в одну группу. Если какая-либо из групп полностью накрывается другими группами, то ее можно игнорировать. Такую избыточную группу можно не учитывать при составлении минимизированного выражения для булевой функции. Например. N = 2 N = 3 (X, Y) (X, Y, Z)
N = 4 (X1, X2, X3, X4)
Примеры минимизации:
Пример. Минимизировать с помощью карта Карно функцию:
Для данной функции уже была составлена ДНФ: F(x, y, z) = Построим карту Карно для заданной функции:
Минимизируем ДНФ с помощью законов алгебры логики: F(x, y, z) =
1 1 1 1
В процессе минимизации использовали: 1. Закон дополнения - 2. Правило вычеркивания - При минимизации ДНФ разными способами получили одинаковый результат.
Пример 2. Минимизировать на картах Карно функцию f(x1, x2, x3, x4), которая равна 1 на наборах с номерами: 0, 1, 2, 3, 4, 6, 7, 8, 9, 11, 15
Построим двоичные наборы, на которых задана функция
Построим карту Карно для заданной функции:

Таким образом,
ПРАКТИЧЕСКАЯ ЧАСТЬ. 1. Выполнить минимизацию СДНФ или КСНФ, заданных ФАЛ: используя законы алгебры логики графический метод минимизации 2. Выполнить решение заданных ФАЛ с помощью законов алгебры логики.
***Примечание: если преобразования и минимизация выполнены верно, в результате выполнения пп 1 и 2 должен получиться одинаковый результат
Законы булевой алгебры 1. Переместительный закон
2. Сочетательный закон
3. Распределительный закон
4. Закон нулевого множества
5. Закон универсального множества
6. Закон повторения
Правило приведения подобных членов в выражении:
7. Закон поглощения
8. Законы для инверсии а) Закон дополнения б) Закон склеивания
в) Закон двойного отрицания г) Правило вычеркивания
г) Правило де-Моргана
Следствие: правило де-Моргана - Шеннона: Для того, чтобы взять отрицание от какого-либо выражения, надо все знаки логического сложения заменить знаками логического умножения, все знаки логического умножения заменить знаками логического сложения, и взять отрицания всех членов выражения. Выражение одних элементарных функций через другие:
12 |










 Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú 


 )
)













 0
0 0
0 1
1 1
1 1
1 1
1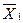



 00
00 0
0




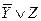

 или
или 
 00
00 01
01 00
00 1
1 1
1









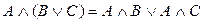















 или
или 
 (или
(или 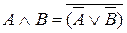 )
) (или
(или 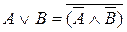 )
)