 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задачи к контрольным заданиям
Статика Задача С1 Конструкция состоит из жесткого угольника и стержня, которые в точке
Рис. С1.0 Рис. С1.1
Рис. С1.2 Рис. С1.3
Рис. С1.4 Рис. С1.5
Рис. С1.6 Рис. С1.7
Рис. С1.8 Рис. С1.9
Внешними связями, наложенными на конструкцию, являются в точке На каждую конструкцию действуют: пара сил с моментом Определить реакции связей в точках Таблица С1
Таблица С1а
Указания. Задача С1 – на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении можно или рассмотреть сначала равновесие всей системы в целом, а затем равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, учесть, что ее реакция представляется силой, модуль и направление которой неизвестны, и парой сил, момент которой тоже неизвестен. Пример С1. На угольник Дано: Определить: реакции в точках Решение: 1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня
Рис. С1
2. Теперь рассмотрим равновесие угольника (рис. С1,в). На него действуют сила давления стержня
При вычислении момента силы Ответ: Кинематика Задача К1 Под номером К1 помещены две задачи К1а и К1б, которые надо решить. Задача К1а. Точка Найти уравнение траектории точки; для момента времени
Рис. К1.0 Рис. К1.1 Рис. К1.2
Рис. К1.3 Рис. К1.4 Рис. К1.5
Рис. К1.6 Рис. К1.7 Рис. К1.8
Задача К1б. Точка движется по дуге окружности радиуса Таблица К1
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени Пример К1а. Даны уравнения движения точки в плоскости
( Определить уравнение траектории точки; для момента времени Решение: 1. Для определения уравнения траектории точки исключим из заданных уравнений движения время
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. К1,а):
Для момента времени 3. Аналогично найдем ускорение точки:
Для момента времени 4. Касательное ускорение найдем, дифференцируя по времени равенство:
Получим
откуда
Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3) и ,(4). Подставив в (5) эти числа, найдем сразу, что при 5. Нормальное ускорение точки 6. Радиус кривизны траектории Ответ: Пример К1б. Точка движется по дуге окружности радиуса Определить скорость и ускорение точки в момент времени Решение: Определяем скорость точки:
При Ускорение находим по его касательной и нормальной составляющим:
Изобразим на рис. К1,б векторы Ответ: Задача К2 Плоский механизм состоит из стержней 1–4 и ползуна Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол
Рис. К2.0 Рис. К2.1
Рис. К2.2 Рис. К2.3
Рис. К2.4 Рис. К2.5
Рис. К2.6 Рис. К2.7
Рис. К2.8 Рис. К2.9
Определить ускорение точки Построение чертежа начинать со стержня, направление которого определяется углом Заданные угловую скорость и угловое ускорение считать направленными против часовой стрелки, а заданную скорость Указания. Задача К2 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности. Таблица К2
Пример К2.
Определить: Решение: 1. Строим положение механизма в соответствии с заданными углами и выбранным масштабом длин (рис. К2,б; на этом рисунке изображаем все векторы скоростей).
3. Определяем
Чтобы вычислить
Так как точка
4. Определяем
5. Определяем
где численно
Ответ: КОНТРОЛЬНЫЕ ВОПРОСЫ Задача С1 1) Основные виды силовых воздействий и их свойства: – сосредоточенная сила (проекции силы на оси; момент силы относительно точки как характеристика вращательного действия силы; величина и знак алгебраического момента; – вращающий момент (пара сил), изображение пары на плоскости, момент пары; – распределенные силы с постоянной интенсивностью (эпюра распределенных сил, приведение к равнодействующей). 2) Силы активные и реакции связей. Внешние закрепления конструкции (подвижный и неподвижный цилиндрические шарниры, скользящая заделка – втулка, жесткая заделка, невесомый стержень, нить, идеальная поверхность). Как направлены реакции этих связей? Сколько неизвестных составляющих реакции имеет каждая из перечисленных связей? В каком случае реакция связи содержит вращающий момент? 3) Виды представленных в конструкциях соединений тел между собой. Метод разбиения. Внутренние двусторонние и односторонние связи. 4) Каковы аналитические условия равновесия произвольной плоской системы сил? 5) Статическая определимость и неопределимость конструкции. Какие дополнительные условия представлены в задаче, которые делают конструкцию статически определимой? Как определяется статическая определимость в сочлененных конструкциях? Задача К1 1) Координатный способ задания движения точки. 2) Определение скорости точки. Нахождение скорости при координатном способе задания движения. 3) Определение ускорения. Разложение ускорения на касательную и нормальную составляющие. 4) Естественный способ изучения движения. Определение кинематических характеристик в естественных координатах. Задача К2 1) Виды движений различных звеньев плоского механизма задачи К2. 2) Поступательное движение. 3) Вращательное движение вокруг неподвижной оси (центра 4) Плоскопараллельное движение. Мгновенный центр скоростей и его свойства. Как найдены МЦС звеньев механизма задачи? 5) Как формулируется теорема о проекциях скоростей двух точек тела? Как она используется для нахождения скоростей различных точек механизма? Библиографический список 1. Никитин Н.Н. Курс теоретической механики: учебник для машиностроит. и приборостроит. спец. вузов / Н.Н. Никитин. – М.: Высш. шк., 1990. 607 с. 2. Бутенин Н.В. Курс теоретической механики: в 2х т. / Н.В. Бутенин, Я.Л. Лунц, Д.Р. Меркин. – СПб.: Лань, 2002. 736 с. 3. Тарг С.М. Краткий курс теоретической механики / С.М. Тарг. – М: Высш. шк., 2008. 416 с. 4. Цывильский В.Л. Теоретическая механика / В.Л. Цывильский. – М: Высш. шк., 2008. 368 с. 5. Переславцева Н.С. Теоретическая механика: учеб. пособие / Н.С. Переславцева, Н.П. Бестужева. – Воронеж: ВГТУ, 2009. – 157 с. 6. Мещерский И.В. Задачи по теоретической механике / И.В. Мещерский. – СПб.: Лань, 2001. 448 с. 7. Сборник заданий для курсовых работ по теоретической механике: учеб. пособие для техн. вузов / под ред. А.А. Яблонского. – М.: Интеграл-Пресс, 2006. 384 с. содержание
Программа курса . . . . . . . . . . . . . . . . . . . . . . . 1 Статика . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Кинематика. . . . . . . . . . . . . . . . . . . . . . . . . 3 Кинематика твердого тела. . . . . . . . . . . . . . . . . 4 Содержание контрольных заданий, выбор вариантов, порядок выполнения работ, общие пояснения к тексту задач . . . . . . . . . . . . . . . . . 5 Принятые обозначения. . . . . . . . . . . . . . . . . . . . 7 Задачи к контрольным заданиям . . . . . . . . . . . . . . 10 Статика. Задача С1 . . . . . . . . . . . . . . . . . . . . 10 Кинематика. Задача К1. . . . . . . . . . . . . . . . . . 16 Задача К2. . . . . . . . . . . . . . . . . . 22 Контрольные вопросы. . . . . . . . . . . . . . . . . . . . 29 Библиографический список. . . . . . . . . . . . . . . . . 31
Программа, методические указания и контрольное задание № 1 (статика, кинематика) по дисциплине «Теоретическая механика» для бакалавров всех направлений заочной и заочной ускоренной форм обучения
Составители: Переславцева Наталья Сергеевна Бестужева Наталья Петровна
В авторской редакции
Компьютерный набор Н.С. Переславцевой
Подписано к изданию 30.10.2012. Уч.-изд. л. 1,9.
ФГБОУ ВПО «Воронежский государственный технический университет» 394026 Воронеж, Московский просп., 14 |



 или соединены друг с другом шарнирно (рис. С1.0–С1.5), или свободно опираются друг о друга (рис. С1.6–С1.9).
или соединены друг с другом шарнирно (рис. С1.0–С1.5), или свободно опираются друг о друга (рис. С1.6–С1.9).




 или шарнир, или жесткая заделка; в точке
или шарнир, или жесткая заделка; в точке  или гладкая плоскость (рис. С1.0 и С1.1), или невесомый стержень
или гладкая плоскость (рис. С1.0 и С1.1), или невесомый стержень 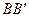 (рис. С1.2 и С1.3), или шарнир (рис. С1.4– С1.9); в точке
(рис. С1.2 и С1.3), или шарнир (рис. С1.4– С1.9); в точке  или невесомый стержень
или невесомый стержень  (рис. С1.0, С1.3, С1.8), или шарнирная опора на катках (рис. С1.7).
(рис. С1.0, С1.3, С1.8), или шарнирная опора на катках (рис. С1.7).
 , равномерно распределенная нагрузка интенсивности
, равномерно распределенная нагрузка интенсивности 
 и еще две силы. Эти силы, их направления и точки приложения указаны в табл. С1; там же в столбце «Нагруженный участок» указано, на каком участке действует распределенная нагрузка (например, в условиях № 1 на конструкцию действуют сила
и еще две силы. Эти силы, их направления и точки приложения указаны в табл. С1; там же в столбце «Нагруженный участок» указано, на каком участке действует распределенная нагрузка (например, в условиях № 1 на конструкцию действуют сила  под углом 60° к горизонтальной оси, приложенная в точке
под углом 60° к горизонтальной оси, приложенная в точке  , сила
, сила  под углом 30° к горизонтальной оси, приложенная в точке
под углом 30° к горизонтальной оси, приложенная в точке  , и нагрузка, распределенная на участке
, и нагрузка, распределенная на участке 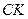 ).
). ,
,  м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С1а.
м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С1а.


 Сила
Сила кН
кН кН
кН кН
кН кН
кН



 (
(  ), конец
), конец  (рис. С1,а). Стержень имеет в точке
(рис. С1,а). Стержень имеет в точке  , а к угольнику – равномерно распределенная на участке
, а к угольнику – равномерно распределенная на участке  нагрузка интенсивности
нагрузка интенсивности  и пара с моментом
и пара с моментом  .
. кН,
кН, 
 ,
,  и изобразим действующие на стержень силы: силу
и изобразим действующие на стержень силы: силу  , направленную перпендикулярно стержню, и составляющие
, направленную перпендикулярно стержню, и составляющие 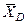 и
и  реакции шарнира
реакции шарнира  (1)
(1) (2)
(2) (3)
(3)
 , направленная противоположно реакции
, направленная противоположно реакции  , приложенной в середине участка
, приложенной в середине участка  кН), пара сил с моментом
кН), пара сил с моментом  и
и  , и пары с моментом
, и пары с моментом  . Для этой плоской системы сил тоже составляем три уравнения равновесия:
. Для этой плоской системы сил тоже составляем три уравнения равновесия: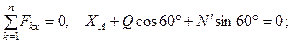 (4)
(4) (5)
(5)
 . (6)
. (6) и
и 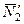 и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1)–(6), найдем искомые реакции. При решении учитываем, что
и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1)–(6), найдем искомые реакции. При решении учитываем, что  в силу равенства действия и противодействия.
в силу равенства действия и противодействия. кН,
кН,  кН,
кН,  кН,
кН,  кН,
кН,  кН,
кН, 
 ,
,  , где
, где  и
и  выражены в сантиметрах,
выражены в сантиметрах,  – в секундах.
– в секундах.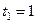 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.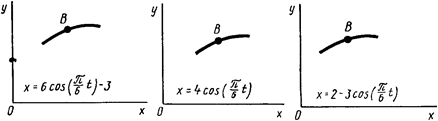



 Зависимость
Зависимость  м по закону
м по закону  , заданному в табл. К1 в столбце 5 (
, заданному в табл. К1 в столбце 5 (  – в метрах,
– в метрах,  — расстояние точки от некоторого начала
— расстояние точки от некоторого начала  и
и  , считая, что точка в этот момент находится в положении
, считая, что точка в этот момент находится в положении 







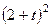






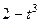
 ,
, 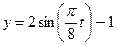
 :
: . (1)
. (1) ,
,  ,
, следовательно,
следовательно, .
.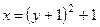 . (2)
. (2) 2. Скорость точки найдем по ее проекциям на координатные оси:
2. Скорость точки найдем по ее проекциям на координатные оси: ,
,  ,
, .
.
 ,
, 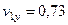

 ,
,  ,
,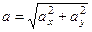 .
.
 ,
, 
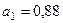

 ,
, . (5)
. (5)
 . Подставляя сюда найденные при
. Подставляя сюда найденные при  и
и 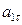 , получим, что
, получим, что 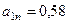
 . Подставляя сюда числовые значения
. Подставляя сюда числовые значения  и
и  при
при  см.
см. , (
, (  .
.
 .
.
 ,
, ,
, .
. При
При 
 ,
, 
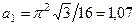
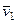 и
и  , учитывая знаки и считая положительным направление от
, учитывая знаки и считая положительным направление от 
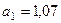
 и
и  шарнирами. Точка
шарнирами. Точка  . Длины стержней равны соответственно
. Длины стержней равны соответственно  м,
м,  м,
м,  м,
м, 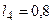 м. Положение механизма определяется углами
м. Положение механизма определяется углами  . Значения этих углов и других заданных величин указаны в табл. К2. Точка
. Значения этих углов и других заданных величин указаны в табл. К2. Точка  на рис. К2.7 – К2.9 в середине соответствующего стержня. Угловое ускорение стержня 1
на рис. К2.7 – К2.9 в середине соответствующего стержня. Угловое ускорение стержня 1  с-1.
с-1. на рис. К2.8 отложить от
на рис. К2.8 отложить от  против хода часовой стрелки, а на рис. К2.9 – по ходу часовой стрелки и т.д.).
против хода часовой стрелки, а на рис. К2.9 – по ходу часовой стрелки и т.д.).



 ; ползун с направляющими для большей наглядности изобразить так, как в примере К2 (см. рис. К2б).
; ползун с направляющими для большей наглядности изобразить так, как в примере К2 (см. рис. К2б). – от точки
– от точки  (на рис. К2.5– К2.9).
(на рис. К2.5– К2.9).


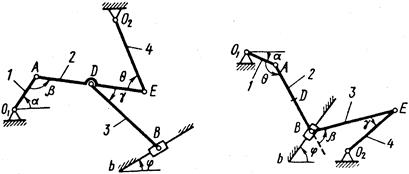
 Механизм (рис. К2,а) состоит из стержней 1, 2, 3, 4 и ползуна
Механизм (рис. К2,а) состоит из стержней 1, 2, 3, 4 и ползуна  Дано:
Дано:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  с-1,
с-1,  с-2 (направления
с-2 (направления  и
и 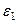 – против хода часовой стрелки).
– против хода часовой стрелки). ,
,  ,
,  ,
,  .
. 2. Определяем
2. Определяем  , можем определить
, можем определить  . Численно:
. Численно: м/с,
м/с,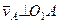 . (1)
. (1) Направление
Направление  ,
,  м/с. (2)
м/с. (2)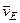 . Точка
. Точка 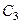 , лежащая на пересечении перпендикуляров к
, лежащая на пересечении перпендикуляров к 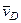 перпендикулярен отрезку
перпендикулярен отрезку  , соединяющему точки
, соединяющему точки  найдем из пропорции:
найдем из пропорции: . (3)
. (3) , заметим, что
, заметим, что  – прямоугольный, так как острые углы в нем равны 30° и 60°, и что
– прямоугольный, так как острые углы в нем равны 30° и 60°, и что  . Тогда
. Тогда 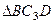 является равносторонним и
является равносторонним и  . В результате равенство (3) дает
. В результате равенство (3) дает м/с,
м/с,  . (4)
. (4) , вращающемуся вокруг
, вращающемуся вокруг  . Тогда, восставляя из точек
. Тогда, восставляя из точек  стержня
стержня  , откуда
, откуда  . Составив теперь пропорцию, найдем, что
. Составив теперь пропорцию, найдем, что ,
,  м/с. (5)
м/с. (5) м, то
м, то с–1. (6)
с–1. (6) (рис. К2,в, на котором изображаем все
(рис. К2,в, на котором изображаем все  векторы ускорений). Точка
векторы ускорений). Точка  ,
, м/с2,
м/с2, м/с2. (7)
м/с2. (7) Вектор
Вектор  направлен вдоль
направлен вдоль  , а
, а 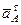 – перпендикулярно
– перпендикулярно  м/с2.
м/с2. м/с,
м/с,  с–1,
с–1,  м/с2.
м/с2. ). Угловая скорость и угловое ускорение вращающихся звеньев. Как направлены и чему равны скорости точек вращающегося тела?
). Угловая скорость и угловое ускорение вращающихся звеньев. Как направлены и чему равны скорости точек вращающегося тела?