 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Алгоритм вычисления собственных векторов линейного оператора 12
1) Зафиксировать произвольный базис 2) Составить и решить (в множестве действительных или комплексных чисел) характеристическое уравнение (3). Его действительные корни 3) При каждом найденном собственном значении Пример 2. Задана матрица
некоторого линейного оператора в базисе Решение.Матрица линейного оператора в базисе
Вычислим определитель:
Итак, получаем следующее характеристическое уравнение оператора
Его корни – собственные значения (решаем квадратное уравнение):
Алгебраическая кратность каждого собственного значения равна одному, так как каждый корень характеристического уравнения повторяется единожды. Соответствующая однородная система (2) имеет вид
Полагая в системе (5)
(удаляем из однородной системы второе уравнение, так как оно равносильно первому уравнению), общее решение которой имеет вид
Находим соответствующую фундаментальную систему решений (положим число
Аналогично положим в системе (5)
(удаляем из однородной системы первое уравнение, так как оно равносильно второму уравнению), общее решение которой имеет вид
Находим соответствующую фундаментальную систему решений (положим число
В заключение, выполним проверку. Убедимся в справедливости равенств
Имеем
Пример 3. Задана матрица
некоторого линейного оператора в базисе Решение.Матрица линейного оператора в базисе
Разложим определитель по первой строке:
Итак, получаем следующее характеристическое уравнение оператора
Его корни – собственные значения:
записанные с учетом алгебраических кратностей. Алгебраическая кратность Соответствующая однородная система (2) имеет вид
Полагая в системе (6)
Решим полученную однородную систему при помощи метода Гаусса. Составляем основную матрицу этой системы и при помощи элементарных преобразований приводим ее к ступенчатому виду
Ранг полученной матрицы равен 1, в качестве базисной переменной удобно взять переменную
Находим соответствующую фундаментальную систему решений. Положим сначала
Положим затем
Вектор-столбцы Аналогично, положив в системе (6)
Решим полученную однородную систему при помощи метода Гаусса. Составляем основную матрицу этой системы и при помощи элементарных преобразований приводим ее к ступенчатому виду
Ранг полученной ступенчатой матрицы равен 2, в качестве базисных переменных удобно взять переменные
Положив в общем решении
собственного вектора В заключение, выполним проверку. Убедимся в справедливости равенства
Имеем
Проверка равенств 12 |



 линейного пространства и найти матрицу
линейного пространства и найти матрицу 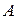 оператора в этом базисе;
оператора в этом базисе; и есть собственные значения оператора;
и есть собственные значения оператора; однородная система (3) будет иметь ненулевые решения. Выделив фундаментальную систему линейно независимых решений, получим либо единственный собственный вектор
однородная система (3) будет иметь ненулевые решения. Выделив фундаментальную систему линейно независимых решений, получим либо единственный собственный вектор  , либо систему r линейно независимых собственных векторов
, либо систему r линейно независимых собственных векторов  оператора, соответствующих собственному значению
оператора, соответствующих собственному значению  .
.
 пространства
пространства  . Найти собственные значения и соответствующие собственные векторы оператора.
. Найти собственные значения и соответствующие собственные векторы оператора. .
. .
. .
.
 (5)
(5) , получим однородную систему
, получим однородную систему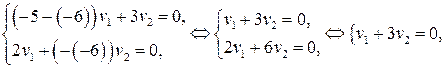
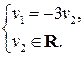
 любым ненулевым числом, для удобства возьмем
любым ненулевым числом, для удобства возьмем  )
) .
. . Получим однородную систему
. Получим однородную систему
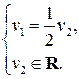
 )
) .
. ,
,  .
.

 . Найти собственные значения и соответствующие собственные векторы оператора.
. Найти собственные значения и соответствующие собственные векторы оператора. .
.
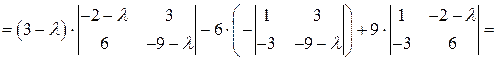




 собственного числа
собственного числа  равна двум, так как данный корень повторяется дважды. Алгебраическая кратность
равна двум, так как данный корень повторяется дважды. Алгебраическая кратность  собственного числа
собственного числа  равна одному, так как данный корень повторяется однократно.
равна одному, так как данный корень повторяется однократно. (6)
(6) , получим однородную систему
, получим однородную систему

 , а в качестве свободных – переменные
, а в качестве свободных – переменные  . Выражая
. Выражая 
 , получим соответственно
, получим соответственно  и вектор-столбец
и вектор-столбец .
. , получим соответственно
, получим соответственно  и вектор-столбец
и вектор-столбец .
. есть координатные вектор-столбцы собственных векторов
есть координатные вектор-столбцы собственных векторов  , отвечающих собственному числу
, отвечающих собственному числу  .
. , получим однородную систему
, получим однородную систему

 , а в качестве свободной – переменную
, а в качестве свободной – переменную  . Выражая
. Выражая 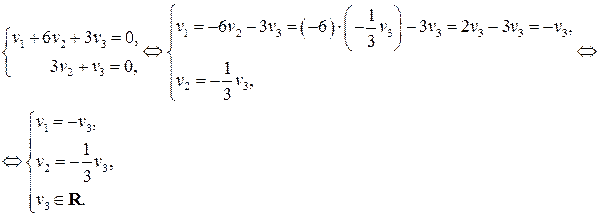
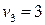 , получим координатный вектор-столбец
, получим координатный вектор-столбец
 .
.
 проводится аналогично.
проводится аналогично.